Community Tip - You can change your system assigned username to something more personal in your community settings. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
A question for the Mathcad historians
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A question for the Mathcad historians
What Mathcad version and year did Odesolve first appear? This is not a test.
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Harvey Hensley wrote:
What Mathcad version and year did Odesolve first appear?
Mathcad 2000.
See please http://twt.mpei.ac.ru/ochkov/Bridge/Bridge_eng.htm
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This is not a test.
That's a relief, because I would fail ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Harvey Hensley wrote:
What Mathcad version and year did Odesolve first appear?
Mathcad 2000.
See please http://twt.mpei.ac.ru/ochkov/Bridge/Bridge_eng.htm
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Valery. I saw a set of problems solved prio to that and I wondered why odesolve hadn't been used, then I suspected that it may not have been available.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Harvey Hensley wrote:
Thanks Valery. I saw a set of problems solved prio to that and I wondered why odesolve hadn't been used, then I suspected that it may not have been available.
You welcome!
Mathcad 2000 with odesolve can solve only one ODE- a Cauchy and boundary problems.
Mathcad 2001 can solve a system of ODEs too - but only a Cauchy problem.
But a boundary problem of ODEs with big error! Mathcad 15 and Mathcad Prime too![]()
See please - t.end:=3
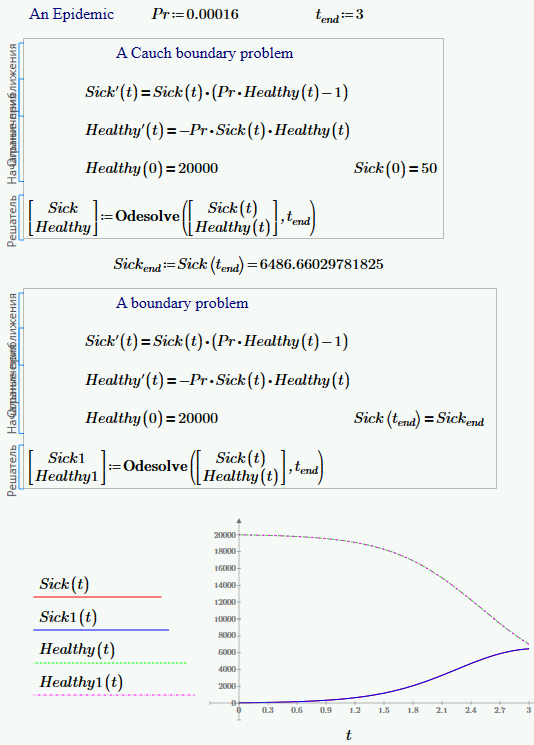
and t.end:=4
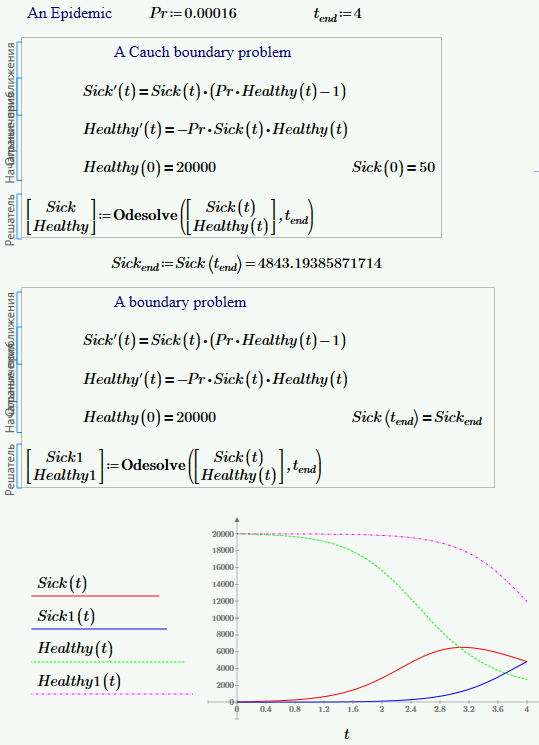
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery,
Unless you have some people dying, the sum of the sick and healthy should remain constant. Thus, their derivaties should be the same except for sign. I think if you get the rates corrected, odesolve will work fine.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There are dead. This is one old model, which was solved back in the DOS versions of Mathcad on the difference scheme, and not through the solving ode.
Sorry Sick=x Healthe=y. A main is the wrong work of the odesolve by boundary problem solution.
Or I do someone wrong?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There are dead. This is one old model, which was solved back in the DOS versions of Mathcad on the difference scheme, and not through the solving ode.
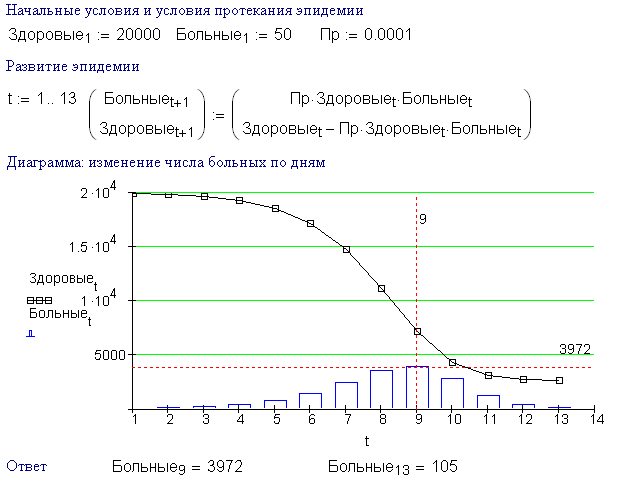
Sorry Sick (Больные) = x Healthe (Здоровые) = y. A main is the wrong work of the odesolve by boundary problem solution.
Or I do someone wrong?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The problem appears to be that the system has more than one initial condition that can lead to the number of Sick at the end time. If instead you specify the initial Healthy and Sick and the final Dead, then the boundary solution is the same as the initial value solution. So I don't think it's really a problem with the solver, just a multiple answer system.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks!
But I think it is one YEMB!
The shooting method solves this problem.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
But I think it is one YEMB!
No! Here you see two different solutions to your problem. They both stick to the equations and adhere to your boundery condition. For the one is Sick(12)=209 in the upgoing branch before the maximum, for the other its after the max. But both are valid solutions to your problem. One method finds the one, another method finds the other. Harvey showed one way to force one particular solution by introducing a third function to the system.
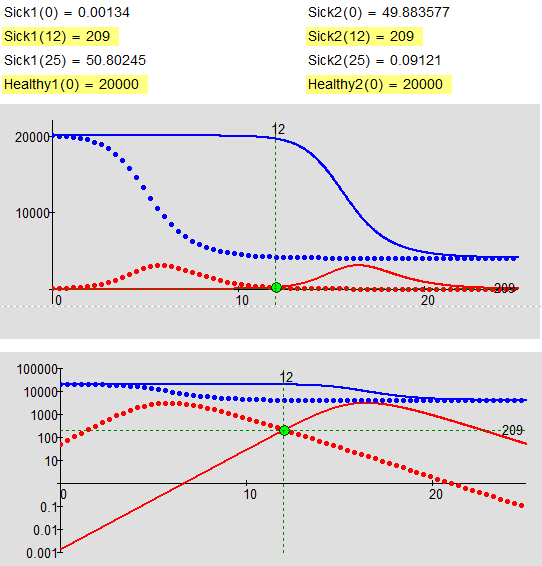
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It wasn't the introduction of the Dead function alone. When I did that but still specified the Sick at tend, the result was still the solution to a different set of initial conditions. I checked those initial conditions by running as an initial value problem and they resulted in the right value for Sick(tend). Changing to specifying the Dead at tend produced the original solution to the initial value problem. Probably that specification has only one solution. The original specification definitely has more than one solution. I think it is just a fortunate coincidence that the shooting method gets the solution desired. Odesolve actually uses sbval (shooting method), but may have some different tolerance or initial step size?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Harvey Hensley wrote:
It wasn't the introduction of the Dead function alone.
Yes, I was simplifying.
It looks to me that the original question has just a finite number of solutions, best guess: there are exactly two.
So it doesn't seem to be possible to add a constraint to the odesolve block to chose the desired one.
Things like Sick(0)>1 or Sick´(12)<0 obviously fail. So it looked to me that the skilled introduction of a third function would be the only way to do the job.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The split happens when Sick is at its max.
Not sure if its really an error, as you wrote, or just another possible solution!?
EDIT: Let t.end-->infinity, so we get the conditions Healthy(0)=20000 and Sick(infinity)=0 and the constant solutions Sick(t)=0 and Healthy(t)=20000 will perfectly comply with your equations in a trivial way.
So, as Harvey has already pointed out, its just a multiple answer system, not YEMB (yet another mathcad bug).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
So, as Harvey has already pointed out, its just a multiple answer system, not YEMB (yet another mathcad bug).
By producing an analytical solution for Sick as a function of Health we can see more clearly the multiple solution aspect (see below, where I've used s for Sick and h for Health):
Actually, the situation is slightly more complicated than this - see attached file for more detail.
Alan
Edit: I posted this on 27 August. As of early 30 August it hasn't appeared.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Edit: I posted this on 27 August. As of early 30 August it hasn't appeared.
Now I have no message from this forume...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
Now I have no message from this forume...
Posting works now but will be delayed due to "moderation".
Go to this thread for more information http://communities.ptc.com/message/219570#219570





