Community Tip - You can Bookmark boards, posts or articles that you'd like to access again easily! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
A question on activation energy determination
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A question on activation energy determination
Having a group of experimental data like following
where α is conversion of the reaction under research. some important kinetic parameters like (E/R) are needed to be obtained from above data.
and the following model has to be considered,
Above function will be used to fit the experimental data in order to determine E/R and lncA from slope and interception, respectively.
And this will require that m and n have to be obtained in advance.
according to my solution, lncA, E/R, m and n have to be determined at the same time, I dont know how m and n are got at first.
data are attached
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Shall I force E/R to be a positive value?
That works if you also (as Harvey suggests) force m to be negative
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, m and n have to be determined at the same time, but there's more than enough data points to determine the values of 4 unknowns. However, if E/R and lncA are constants, then there should be a linear relationship between the LHS of your equation and 1/T, and that is not the case.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks a lot
I found that there was a initial guess value sensitive problem for current example (see attached). I dont know whether there is a good method to avoid this.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I found that there was a initial guess value sensitive problem for current example (see attached). I dont know whether there is a good method to avoid this.
You need to vectorise the product alpha^m.(1-alpha)^n otherwise it will evaluate to a single number instead of a vector of numbers. The resulting solution is then more robust to changes in initial guesses as well.
Alan
NB Don't forget to vectorise the expression on the graph also.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You need to vectorise the product alpha^m.(1-alpha)^n otherwise it will evaluate to a single number instead of a vector of numbers.
Oops! ![]() Good catch.
Good catch.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank u very much, Alan
according to your reply, I vertorized the product of alpha^m(1-alpha)^n, and redid the problem.
the process is actually much much more robust than before.
But the E/R is a negtive number, like following
then, I thought maybe I should let n be a negtive number, but no matter what I did, what I got was only improved fitting results, E/R is still negtive.this is a litte unexpected.
Following is what I did. I dont know what a negative E/R means for a thermo-decomposition (or pyrolysis) reaction, and I dont think it makes sense.
(1)
or
(2)
Shall I force E/R to be a positive value?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Shall I force E/R to be a positive value?
That works if you also (as Harvey suggests) force m to be negative
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This data set looks like it is from a batch reactor and it is just one run. The rate expression suggests that the reaction rate depends upon the reactant to the n th power and to the product to the m th power. Products can affect the rates via adsorption terms that reduce the rate, or by a decay term. In either case, m is probably negative and n positive. For typical reactions n < 3 and m should be a small negative number.
I don't think you will be able to determine m and n with these data because the conversion and temperature are correlated. You need several runs with different starting concentrations to determine m and n. If m and n are known, as originally proposed, then you can determine the temperature functions. Also, you might want to try using an integral method instead of the numerical difference method. Numerical diferences can include a lot of error.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
thanks Harvey
I will consider your suggestion
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The results in shishi-3 look bettter than I expected. It appears that m=0, so no effect of the product on the reaction rate. Also, n=.82 may be real, with a first order reaction and some adsorption inhibition by the reactant. The attached worksheet compares the models with m and n estimated as in shishi-3 with a model assuming m=0 and n=1 (i.e. first order without adsorption). The latter model is only slightly less accurate than the model with m and n estimated. However, a second run with a different initial concentration of the reactant could provide a better idea of the value of n.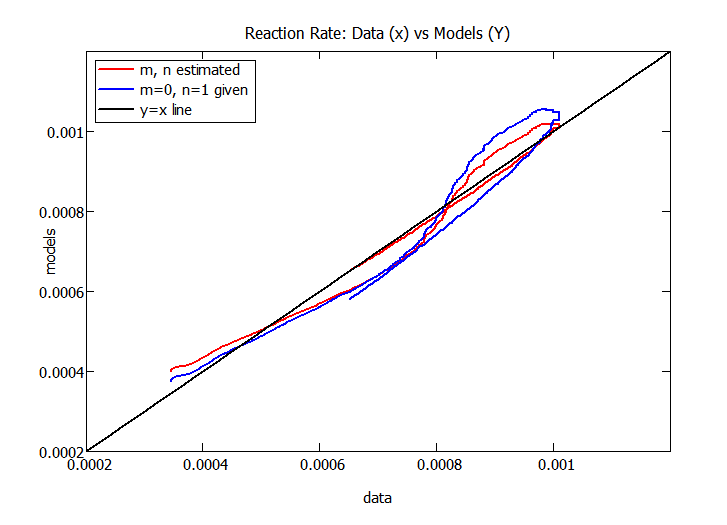
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
could u pls say a few more words on why m should be a negative number?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fan CG wrote:
could u pls say a few more words on why m should be a negative number?
With alpha representing conversion, a term proportional to alpha must represent a product of the reaction because only products increase with conversion. A term like (1-alpha) represents a reactant. Products can be present in the reaction rate only as an inhibitor, not in the mass action terms where only reactants appear. Thus, a product can appear in the denominator of a Langmuir-Hinshelwood adsorption expression. In a power law model such as the one assumed, these denominator terms for products appear as negative powers.





