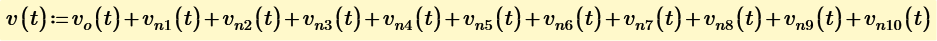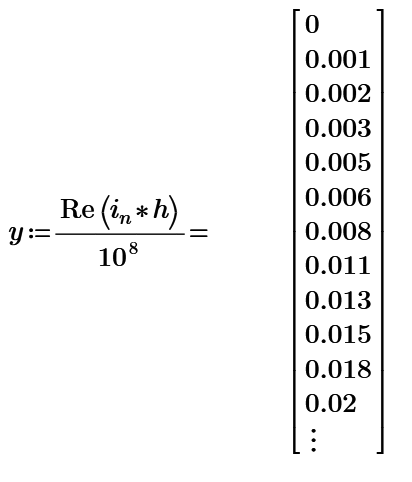Community Tip - Have a PTC product question you need answered fast? Chances are someone has asked it before. Learn about the community search. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
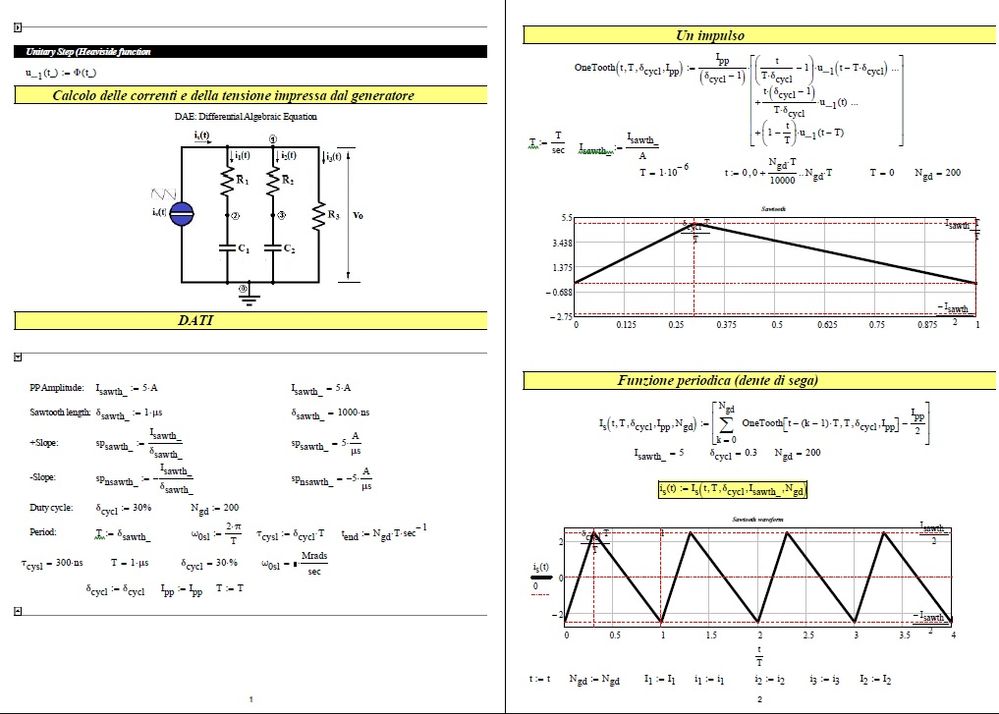
About DAE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
About DAE
Hello everyone!
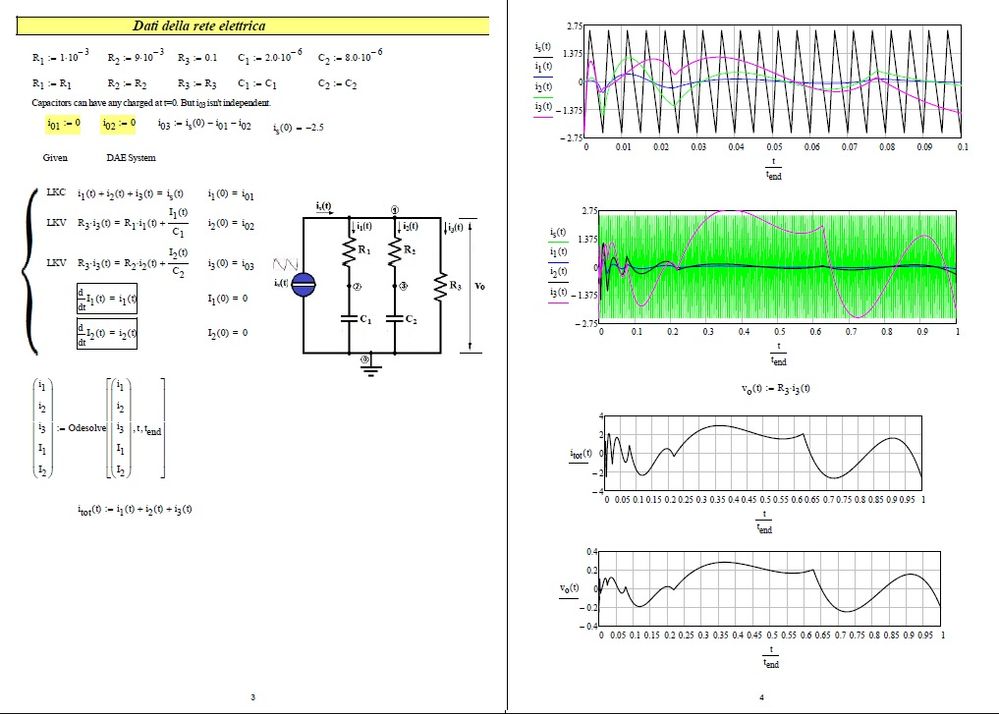
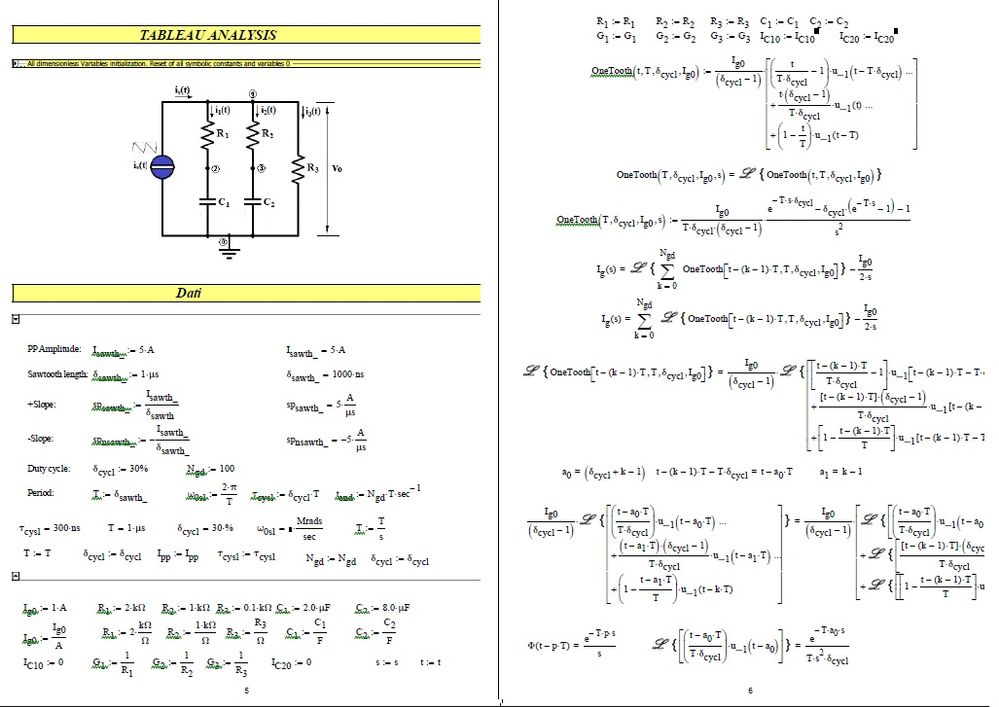
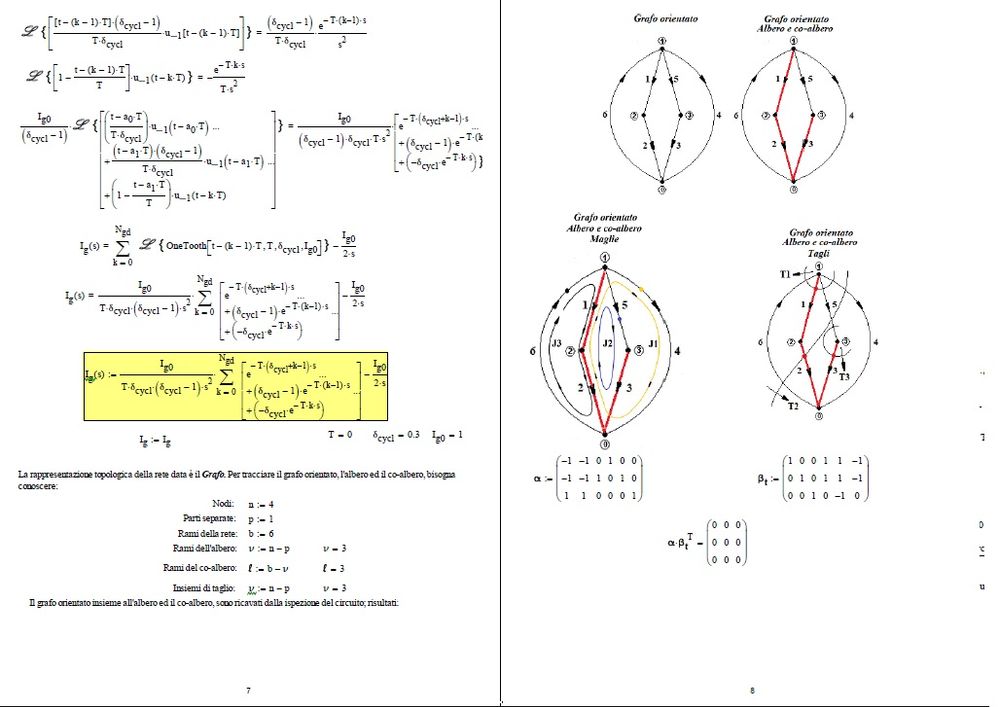
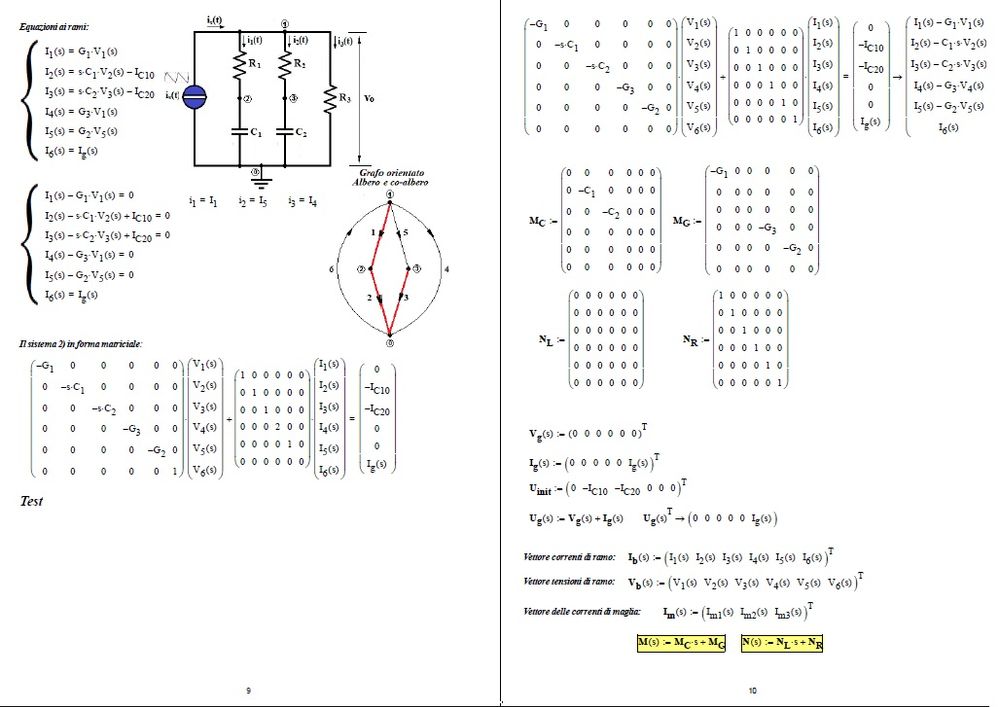
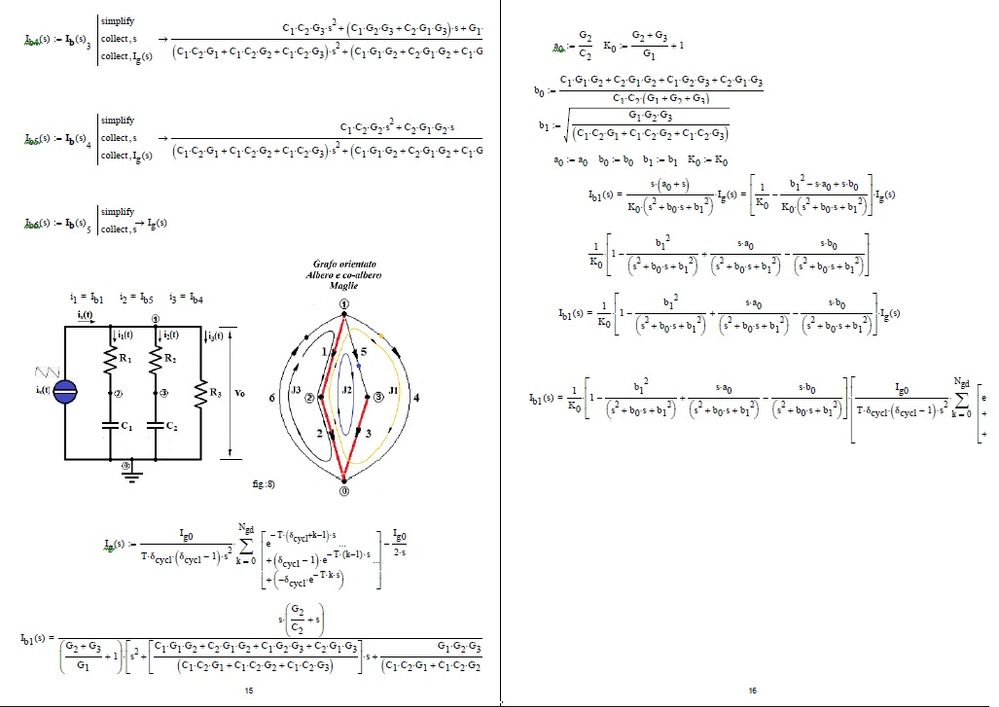
I reworked a worksheet presented by a member of the community I think in 2018 related to the solution of a system of algebraic differential equations with a periodic sawtooth excitation function. I find quite different results depending on how the excitation function is defined. I wonder who's wrong. I enclose the version presented by the member (.mcdx) and my own (dae + 13032023.xmcd).
I await your opinion.
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Make Fourier series of input current wave form.
Get each transient response by inverse Laplace.
Add all response and you can get the answer.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I apologize,
I have attached the wrong file. I am attaching the file that I meant to attach. In my version (dae + 13032023.xmcd), it is necessary to set the duty cycle equal to 9.091% and d.sawth=1.1ms, so that there is correspondence between the two worksheets.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
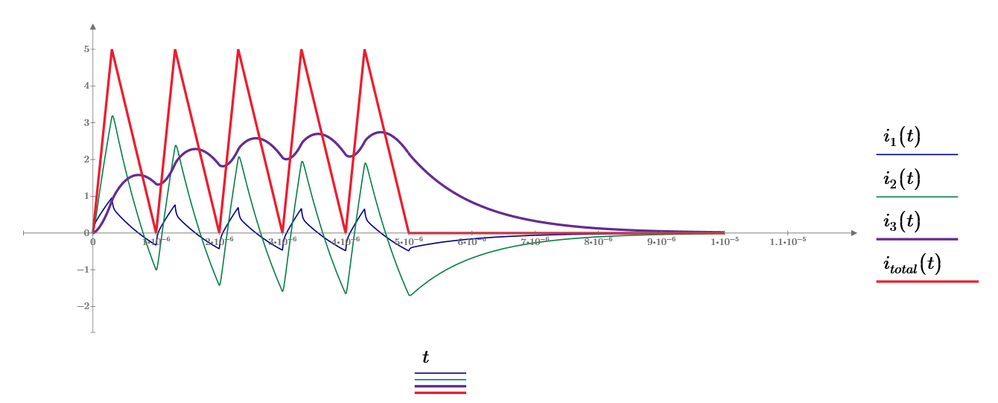
Why is(t) not equal itot(t)? Kirchhoff's Current Law must true even at transient response.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
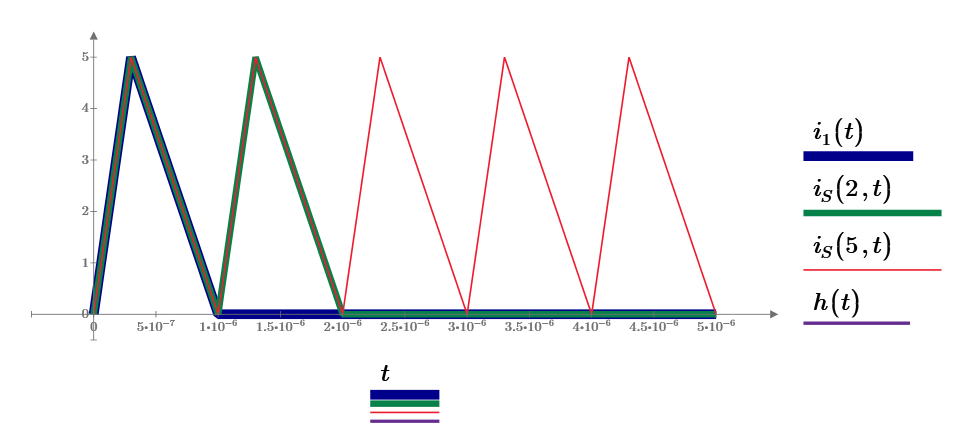
Assuming current source as follows.
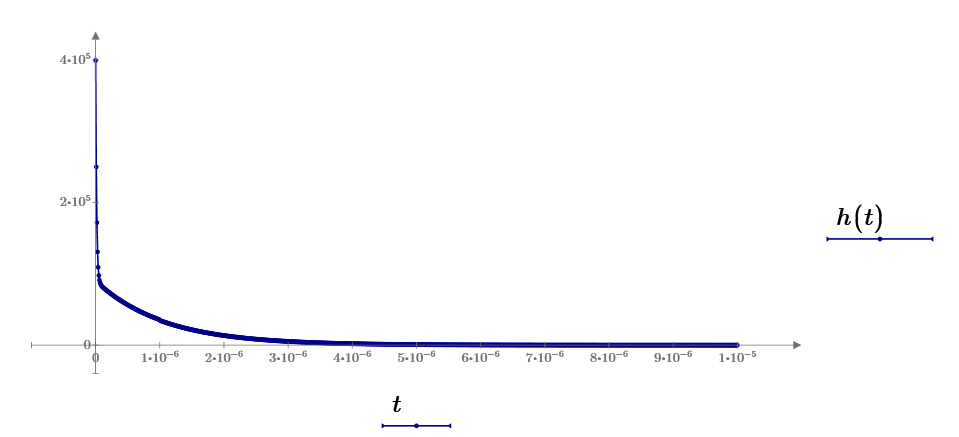
Transfer function of the circuit.
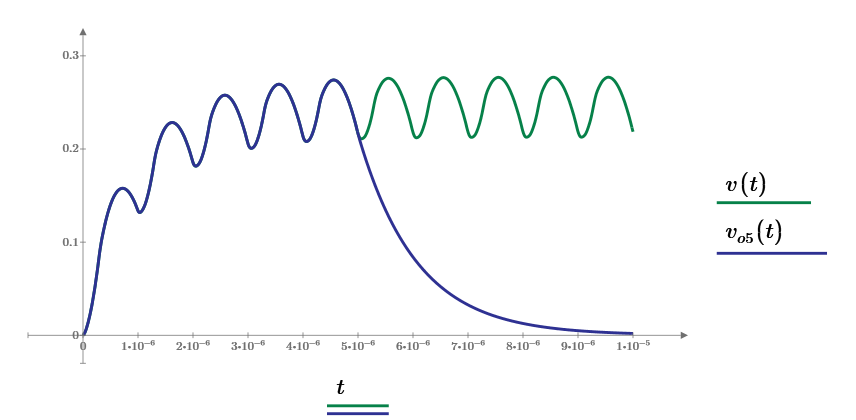
Output voltage of one to five cycles.
Current of each branch circuits. Their total is as same as input current source.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Make Fourier series of input current wave form.
Get each transient response by inverse Laplace.
Add all response and you can get the answer.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
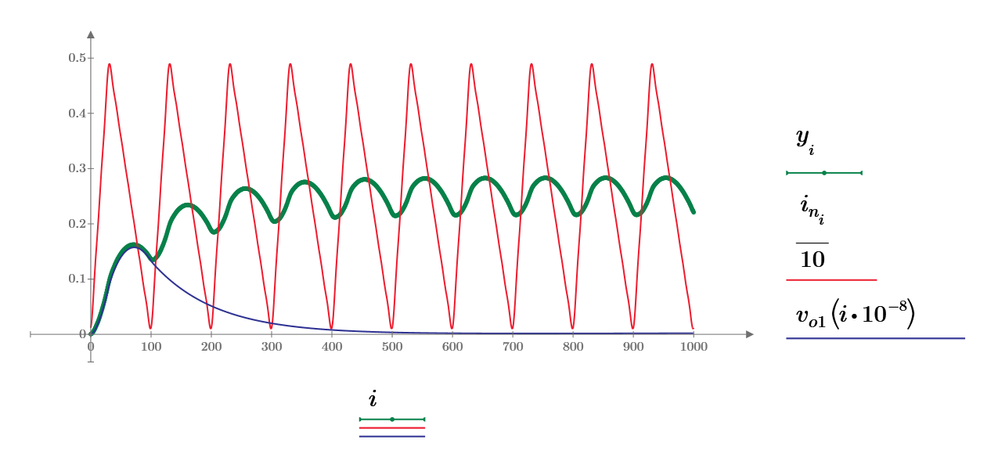
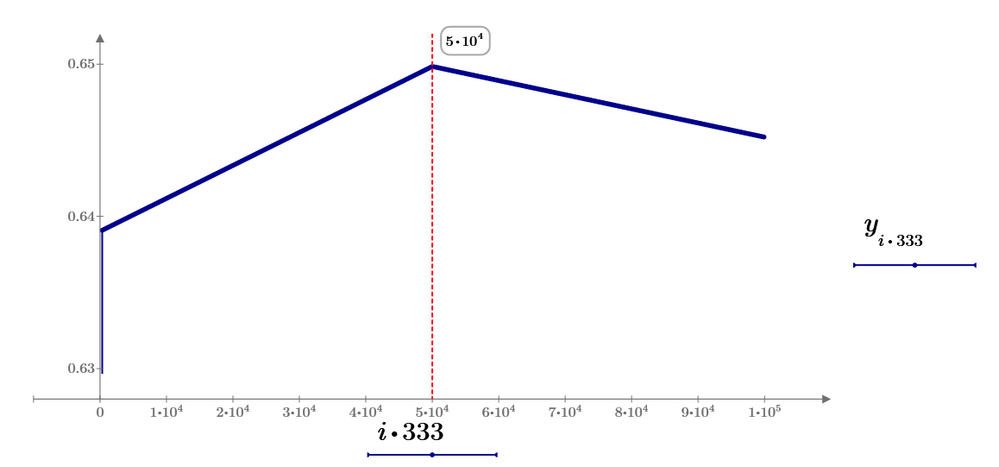
3. Convolution of signals.
Sampling rate: 10 ns.
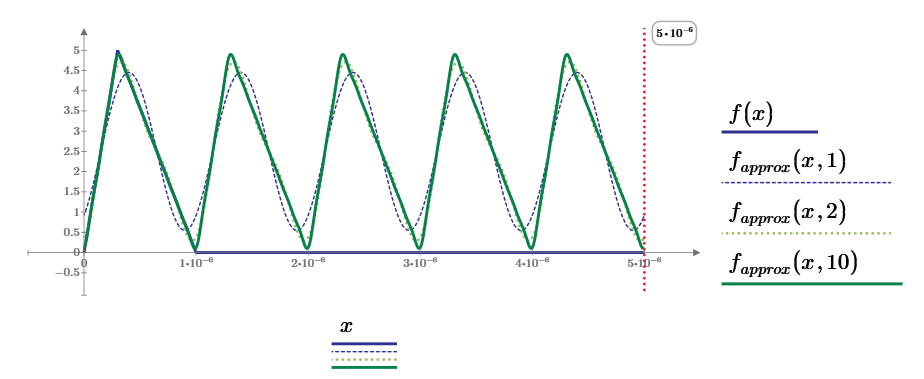
This method can solve for even 1 Hz of input current signal. (But only for few ms as shown in last figure.)
h(t) is almost impulse for 1 Hz input current and output voltage is iin*R3, therefore, 1/10 of input current waveform.
This convolution result is larger than 0.5V at the peak of current signal. This is because the sampling rate is larger to evaluate the output signal more correctly. (Last one use 100ns for sampling rate and convolute 100000 data.)