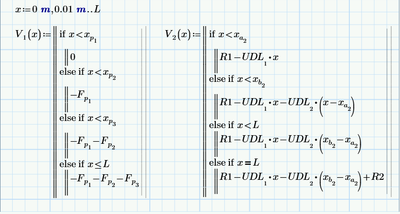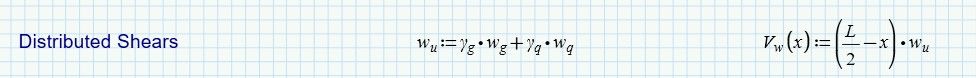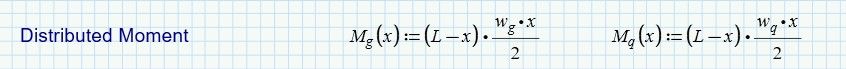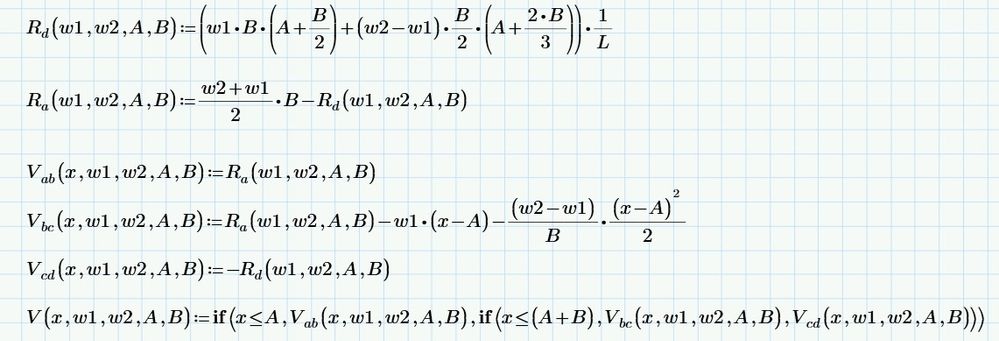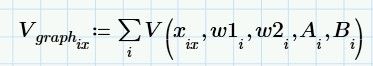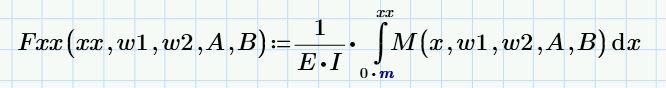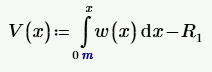- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Beam Bending Shear Force In Mathcad
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Beam Bending Shear Force In Mathcad
Good Evening All,
I am currently in the process of putting together a simply supported beam bending sheet and I was wondering if anyone had any tips of how I can proceed. As you can see from the attached sheet so far I have got the following:
1.) enter section ID to obtain the properties.
2.) enter point loads and location in the vectors
3.)enter UDLs and start / end points in the vectors.
4.)Calculate the reaction forces.
I am now stuck when it comes to the shear force as a function of x. ideally I would want V(x) so i can integrate for the bending moment. From the examples I have seen online alot of the times the shear force is input as a piecewise function (IF x<a... and so on).
Is there anyway so I can get a general expression for shear force that will work no matter what the point loads are / shear forces are and so I don't have to type it out fully each time. Also as this sheet may be used by others I don't want them to have to type in the equations incase of mistakes.
My current thought process would be to possible calculate the shear force as two function V1(x)=point loads and V2(x)=UDLs. I could then define V(x) as the summation of the two to obtain an expression for V(x). But I am open to suggestions and thankyou in advance for any help.
Best Regards,
Callum
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Callum,
Here is a second worksheet that deals with uniform UDL's and Point Loads.
It is Australian Steel Code and beam sizes which should be adjusted for other countries.
Worksheet selects the suitable beam from a table by calculating the capacity of all beams, then picks the size good enough.
In practice Gravity, Live, and Crane loads are increased by factors of Safety that are different for each type of loading.
Also in practice the resistance is diminished by a material factor depending on material.
The sheet has some sample values.
How to handle multiple point loads to get shear equations is demonstrated.
Cheers
Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Callum,
Here is a start. A generic loaded beam worksheet.
Enter four vectors. Calculations adjust as size of entry vectors vary.
A point load can be applied as a short length of uniform loading.
Cheers
Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Callum,
Here is a second worksheet that deals with uniform UDL's and Point Loads.
It is Australian Steel Code and beam sizes which should be adjusted for other countries.
Worksheet selects the suitable beam from a table by calculating the capacity of all beams, then picks the size good enough.
In practice Gravity, Live, and Crane loads are increased by factors of Safety that are different for each type of loading.
Also in practice the resistance is diminished by a material factor depending on material.
The sheet has some sample values.
How to handle multiple point loads to get shear equations is demonstrated.
Cheers
Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Terry,
Thanks for the example sheet, do you have any additional information about what the sheet is doing at each stage. I am relatively new to the software and any additional information would surely be appreciated.
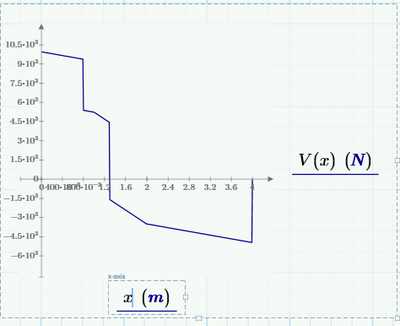
Currently I have gone for this approach and obtained the correct shear force diagram but I would be interested to hear more about the sheet that you have provided.
Best regards,
Callum
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
for example I can't see how the start and end points of the UDLs are calculated or do you convert the UDLs to a point load and only use the UDL's that act over the entire beam.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Callum,
In the file "Choose-UB" the uniform loads are only calculated for udl's over the full beam from 0 to L
In the file "220224-BeamAnalysis_v5-Two_Part_UDL" the loads are by definition of general type and can be partial over a span.
w1, w2 and A can be zero.
The shears are calculated in a more circumspect way.
Then by equations in terms of w1,w2,A,B
and finally filled with values by using the above function on each of the loads summed at each point along the beam
I will need some time to put comments in the files as I will be travelling.
Cheers
Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Terry,
Thanks for getting back to me. I can follow most of what's going on in the sheet choose-UB but I am unsure on some of the calculations still. I am considering the following example:
Beam span L= 4m
Point load one: 4 kN at 0.8 m
Point load two: 6 kN at 1.3m
Point load three: 8 kN at 2.8m
There is a load factor of 1.35 applied to all the point loads.
When I put these values into the formula on the mathcad sheet I get the following:
This is the same as the values obtained in my sheet which are as follows:
This would suggest that the reaction force at x=0m is 13027.5N and the RHS x=4m is 11272.5N. However this would add up to greater than the total load applied to the beam: 18kN.
Thanks,
Callum
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
My bad, I see the existing spreadsheet we use and I am comparing the results with I haven't included the load factor!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Good Morning Terry,
I hope your travels are going well. I was just wondering if you could offer some advice on what the xx refers to in the conjugate beam method. I was under the impression with this method:
Moment on the real beam = Loading on the conjugate beam
Shear on the conjugate beam = slope (theta)
Moment on the conjugate beam = deflection
I am unsure where the "xx" term comes from.
Thanks,
Callum
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Callum,
Finally in a hotel with WiFi.
"xx" is the variable that represents position along the conjugate beam between 0 and "L". Same as "x" in calculation of Shears and Moments along the real beam between 0 and "L".
I did it to make this line more readable.
Cheers
Terry.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Terry,
Thanks for all your help. Appreciate it, I have attached a copy of the finished worksheet if you are interested in it but it may be of limited use as eurocode standard. I am looking to set up something similar for a cantilever beam. I think the shear force and moment diagrams will be easy enough to define piecewise but the conjugate beam method is fairly new to me.
How would one go about this?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
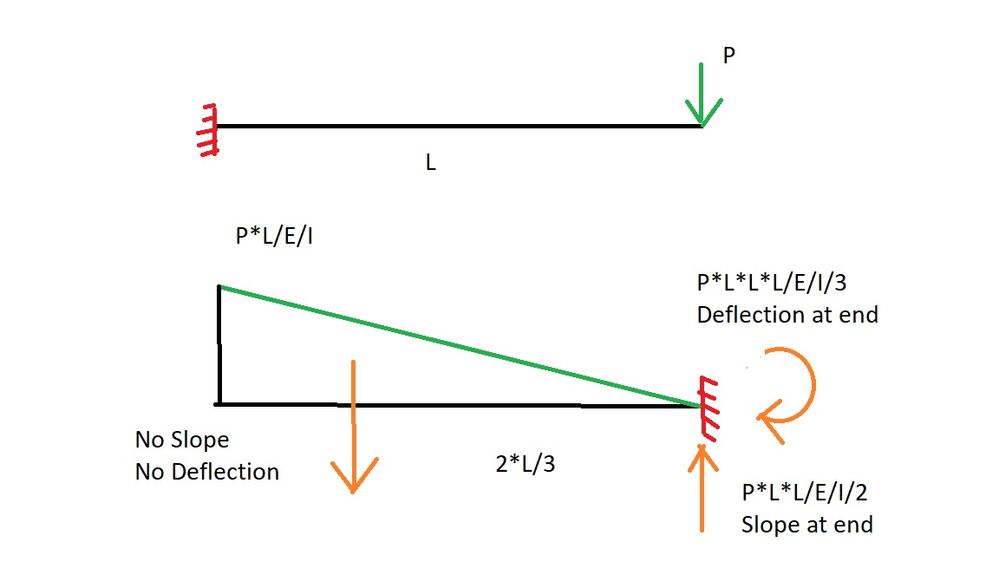
Hi Callum,
For a cantilever swap supports.
At fixed end there is no slope or deflection in real beam this means a free end in the conjugate beam with no shear or moment.
Free end of cantilever has deflection and slope in real beam so is a fixed end in the conjugate.
I will look at your file as it always valuable to see how others approach a problem.
Cheers
Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
By regular old statics, this can be derived:
Your reaction at the first end of the beam is R1. This is also the first value of the shear equation.
Then
I hope this helps!
***
Note: When your loading is a piecewise function, you don't have to use piecewise functions for your shear and bending moment equation, but that changes once you need to use boundary conditions for the angle and deflection equations. You will have to integrate by parts and it gets rather complicated.