Community Tip - Did you get called away in the middle of writing a post? Don't worry you can find your unfinished post later in the Drafts section of your profile page. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Bending Moment and Shear Force Diagram Issues
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Bending Moment and Shear Force Diagram Issues
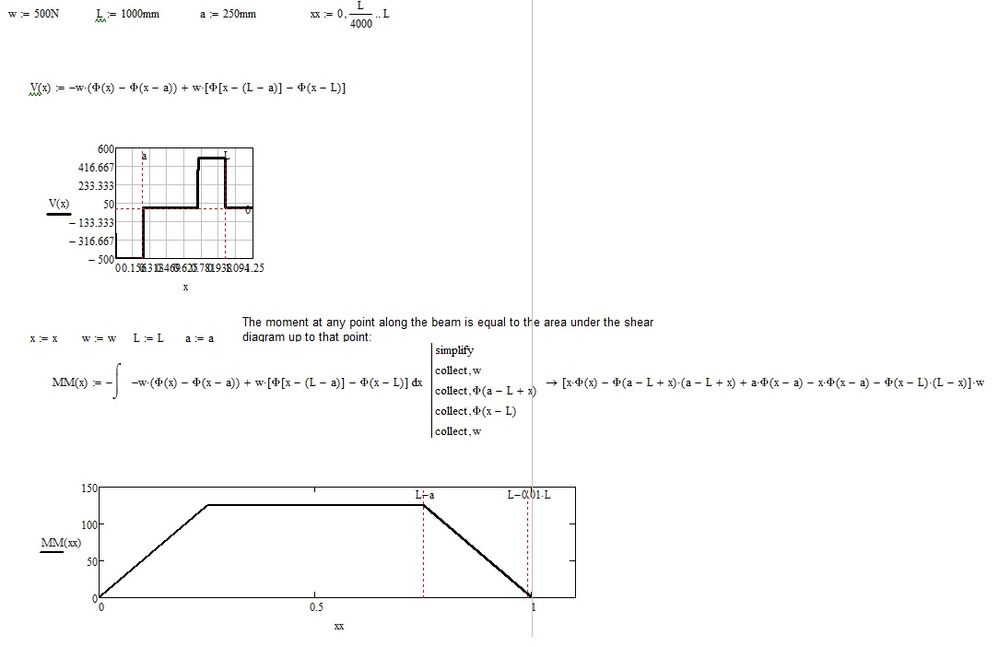
I have started drafting some material for student engineers relating to bending moments and shear forces. Initially, the SF and BM were calculated long hand and the plotted graphs look correct. However, when integration and differentiation is used the graphs are not correct. I am using M15 with Windows 10.
Thanks,
Mike
Solved! Go to Solution.
- Labels:
-
Mechanical_Engineering
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I broke the definite integral into three parts and the defect disappears, look here:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
I have tried this and still get the same error. I have just modified the functions and swapped the 'otherwise' statements to 'if' as shown below:
This has corrected the differentiation error when plotting the shear force diagrams, but there is still an error with the bending moment (MM(x)) plot when integrating V(x).
Thanks,
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Nice work and the graphs are look correct. However, it still isn't clear why the bending moment formula in my worksheet (MM(x)) is returning a zero value for MM(0.9599*m) and above.
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Have you checked the Mathcad Roark's ebook? MM & SF diagrams are plotted for some typical examples
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for the response. Yes I have these but wanted to draft the examples from first principles. The only issue I have is the discontinuity with the bending moment when integrating the shear force.
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I broke the definite integral into three parts and the defect disappears, look here:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Good work and thanks for the effort.
Could you please post the worksheet so I can investigate further?
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
That is a very clever workaround and something I have not seen before. I actually don’t think I have seen the Phi fuction (not sure if that’s the correct name) used ever.
Is the issue in my example due to a discontinuity in the shear force assessment?
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
1) Welcome back, Mike!
Is the issue in my example due to a discontinuity in the shear force assessment?
2) No, its the splitting of the integral in three parts (which shouldn't be necessary) which does the trick. It works OK with the way you defined V(x), too. Have no idea whats going on an why the result suddenly is 0. Tweaking TOL did not change anything.
BTW, using the Heaviside function Phi makes the definition a bit less clear but has the advantage that you can evaluate a function defined that way symbolically, too, if necessary.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Werner and nice example. I have to agree that the Heaviside function Phi makes it a little less clear, but certainly a good tool to have.
The behaviour of the integration suddenly going to zero is certainly strange, especially as differentiating the bending moment for shear force works.
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The behaviour of the integration suddenly going to zero is certainly strange, especially as differentiating the bending moment for shear force works.
Yes, and the Mathcad help only succinctly recommends to split the integration into parts which Francesco did and could make it work.
I tried decreasing TOL and/or changing the method of integration, but in vain.
BTW, you should replace the expression "4wa-wx" in your definition of the bending moment by "w*(L-x)" as otherwise it would yield wrong results if you change "a" from 0.25m to some other value.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
F(x) is a special function often called Heaviside step function or simply unitary step. Its derivative is the Dirac pulse. For example, you can plot functions like the one here depicted:
For the other question, see the answers of the other community members.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for the explanation and help, much appreciated.
Mike