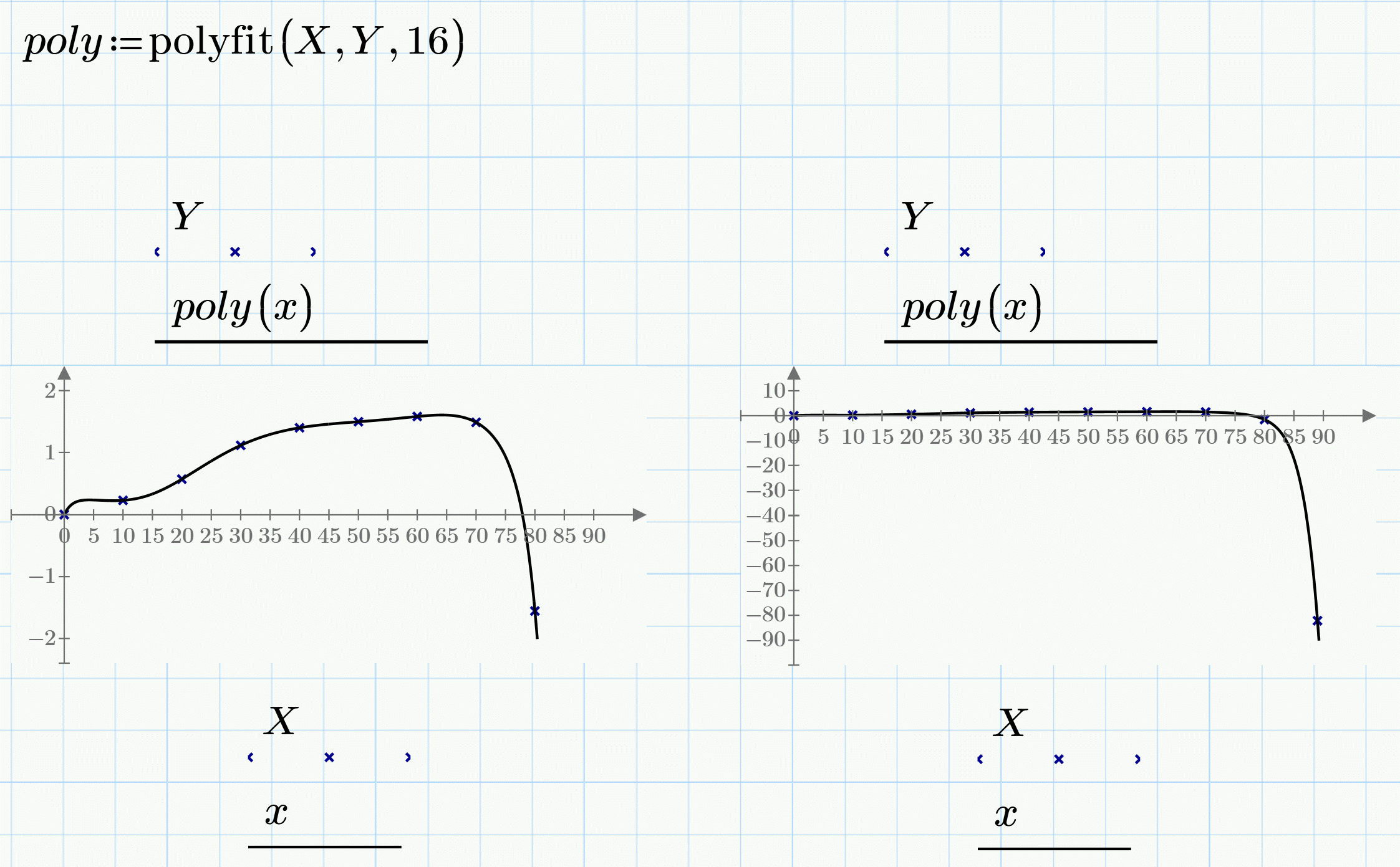Community Tip - You can subscribe to a forum, label or individual post and receive email notifications when someone posts a new topic or reply. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Better Fit
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Better Fit
Hi to all,
In the attached (MCP3) file, can anyone give me some suggestions on how to get a better plot of f(x)? I have tried varying splines but the plot is quite erratic toward the end where as I would expect it to be quite uniform.
Thanks,
Andy
Solved! Go to Solution.
- Labels:
-
Statistics_Analysis
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
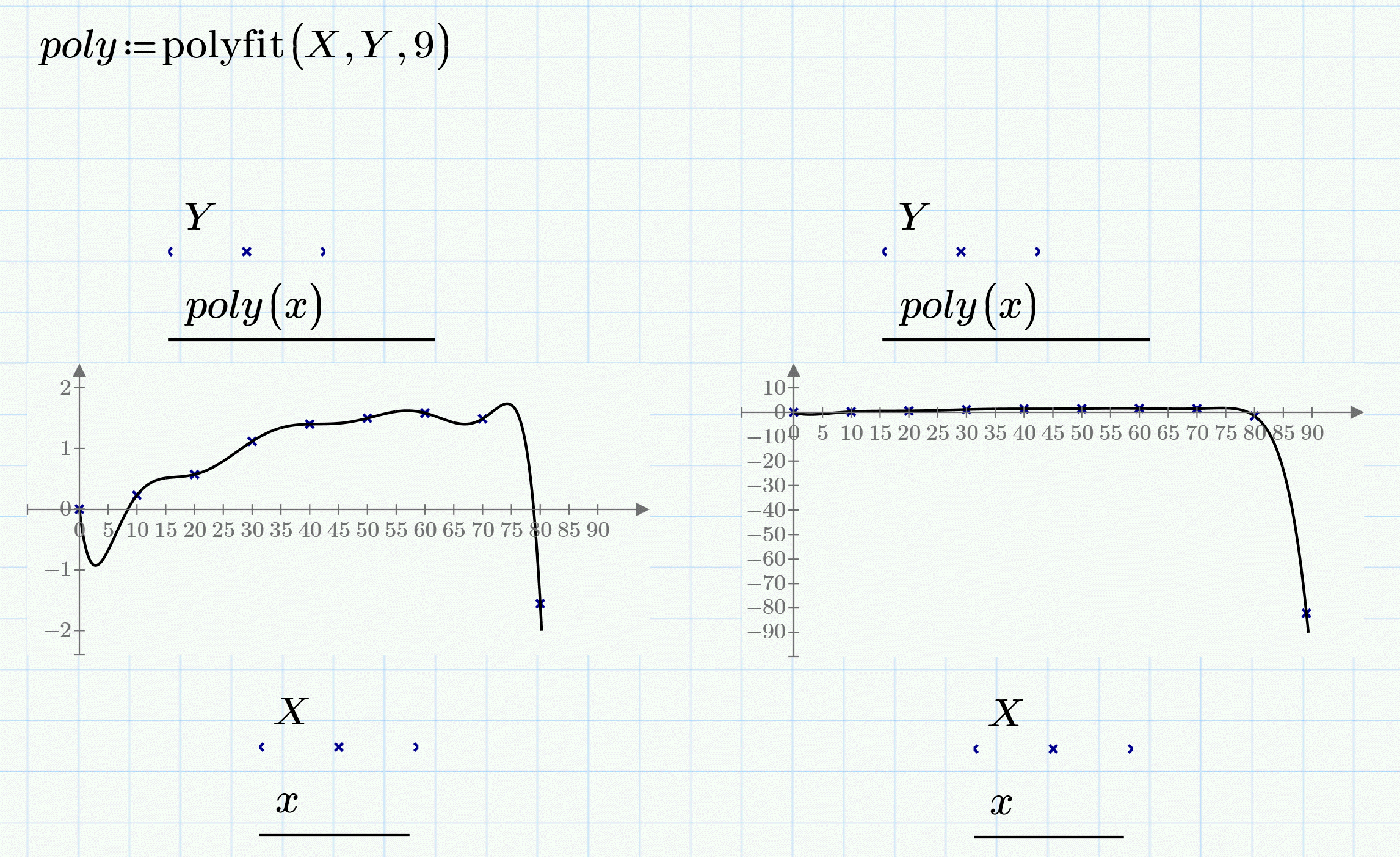
I guess a polynomial of 9th degree is too wavy, too?
Its interesting that we can even demand for a higher order polynomial:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
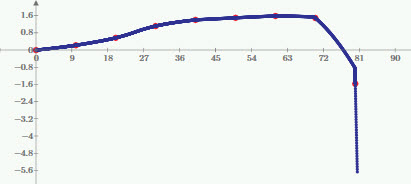
Here's a Schumaker quadratic spline. Bit of a kink at 80, but it's closer than what you had.
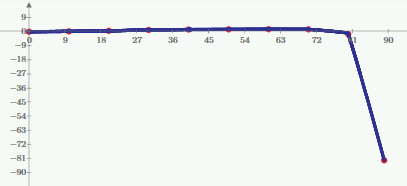
I fit the quadratic and then fit that with a b-spline so you can use it easily.
4.0 and pdf attached.
Also, linear interpolation might be good enough for your data, but there's not much fun in that.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I guess a polynomial of 9th degree is too wavy, too?
Its interesting that we can even demand for a higher order polynomial:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
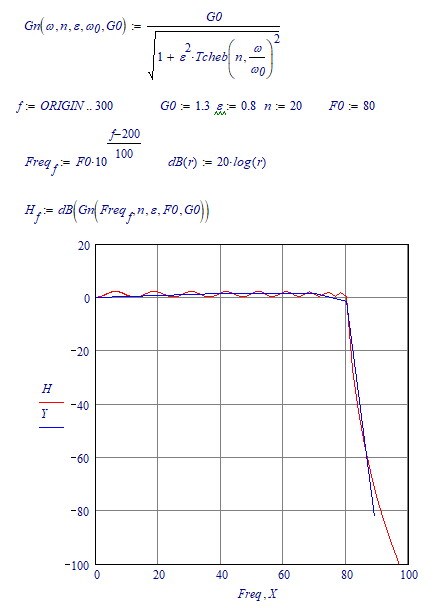
Is this the measured filter characteristic (X in Hz, Y in dB) of an elliptic low-pass filter? https://en.wikipedia.org/wiki/Elliptic_filter
Or a Tshebyshev low-pass filter? https://en.wikipedia.org/wiki/Chebyshev_filter
Then you should be able to find a better fitting with the corresponding filter formulae.
It would also seem then, that you did not measure enough points to accurately catch the passband ripple: considering the very steep roll-off after about 80 Hz I'd expect many more ripples in the passband.
Like this:
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Cheers
Andy