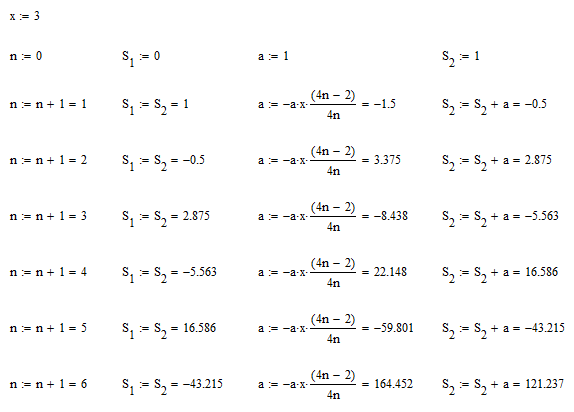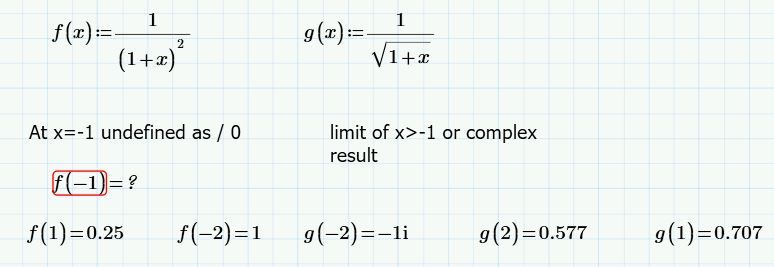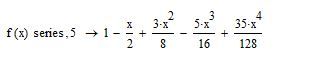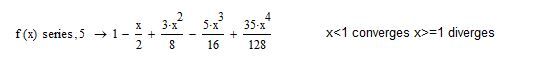Community Tip - Have a PTC product question you need answered fast? Chances are someone has asked it before. Learn about the community search. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Calculations of function (1+x)^(-1/2)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Calculations of function (1+x)^(-1/2)
Hello there,
I have a function that I'm trying to calculate using various methods (in Mathcad).
f(x) = 1/(1+x)^2
I've attached a photo of my code.
The problem is, that for every x from -0.9 to 0.9 the calculations are great, but if i choose x>1 - it gets stuck on an infinite loop (sometimes it even says that it encountered a floating point error). If i try to do a graph of s[0] it also only shows results till x=0.99.
What am I doing wrong?
Thanks in advance.
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'm not familiar with the maclaurin series, so I don't know what you're doing incorrectly. However, take a look at the first several iterations of your While loop:
You can see that S1 and S2 will not be equivalent no mater how many loops you do.
In fact, you can see that "a" grows continuously further from 0. For this loop to end, you need "a" to tend toward zero.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
1. Send please the sheet!
2. You can use functions trace and pause for a debugging the program in Mathcad 15
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
1/ (1+ -1) ^2 is division by zero.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Please, you should be clearer. What should the program calculate? What is the algorithm used?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi
Your email has different equation than in picture, please clarify
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I don't understand what you're doing in the while loop, but it seems unlikely that S1 and S2 would ever be exactly the same. Consider a few options:
- Tools -> Worksheet Options -> Calculation -> uncheck "Use exact equality for comparisons and truncation."
- Change
While S1≠S2
toWhile abs(S2-S1) < {some acceptable level of tolerance} - Would it make sense to change it to this?
While S1<S2
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
@MJG is right. You cannot use condition S1 is not equal to S2 in while loop, when S1, S2 are real numbers. This condition is always TRUE, because of real number representation.
Martin Hanák
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I am very sorry if I did not make myself clear. Not a native english speaker and I have only been studying mathematics mainly in my native language so some terms are new to me. I am uploading a Mathcad file in which my problem exists.
So what are we doing in class is everyone is getting a different function. We have to use maclaurin series and then calculate our given functions using other methods. Then we have to check the "error of calculation"/"the difference in result" from the inbuilt function calculator. I don't know how this method is called in english and I can't seem to find a translation.
I get the idea of what you are saying about not using
while S1 /= S2
I added an example of the same job being done with sin(x) and it's using the same system as me and everything works splendid. I have tens of other examples using the same method for different functions and they all use
while S1 /= S2
I understand that it may not work for my function, but I would like to understand why that is. I hope the two examples in the file that I've added will make more sense of what I am trying to achieve.
Everthing works great with the second function, but with the one I need it stops working if I use
x>0.99
So if I would, lets say, put x=3 (which the answer is quite easily 0.5), the program can't calculate it.
If i'm still not making myself clear, please do tell. I really would like to get to the bottom of this.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'm not familiar with the maclaurin series, so I don't know what you're doing incorrectly. However, take a look at the first several iterations of your While loop:
You can see that S1 and S2 will not be equivalent no mater how many loops you do.
In fact, you can see that "a" grows continuously further from 0. For this loop to end, you need "a" to tend toward zero.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, I believe it just is not appropriate to use such a while in this sort of fuction. Thank you all for your help, cheers.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
The series does not converge rapidly. I have started from scratch.
have changed your cof(n) function to return just the last coeff. You can use it to determine the size of the terms say 42nd and 43 terms.
At this 42 and 43 terms you are working in a 0.09 level of accuracy. You can set it lower but it will take long time.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
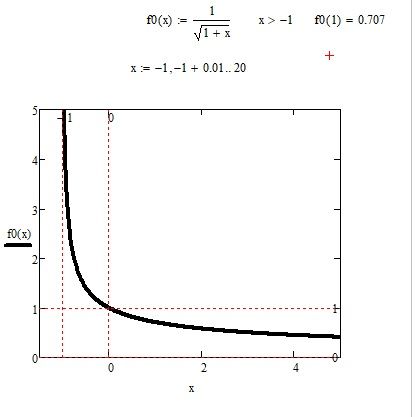
Thank you for trying, but as you can see in the graphs I added, the result is totally different from the function 1/(1+x)^1/2.
While LS(x) and sinx calculates the same. That is what I'm aiming for.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
You need to check the series expansion.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi
Depending on the value of x the series either converges or diverges. At 0.99 it converges. At 1.0 it diverges
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
Thought I would test something.
For extra brownie points a numeric procedure called Levin U transforms can be used to accelerate convergence. Applied to this series with x<1.0 can do it in 19 terms. Summation at 19 terms is 0.6997. Transformed at 19 terms is 0.7082 same as summation at 45 terms
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
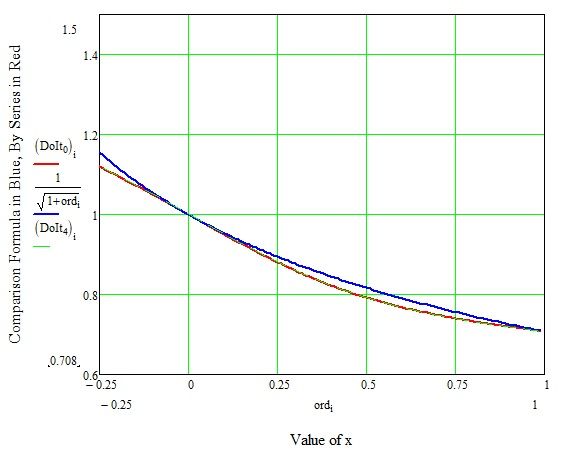
Last file with graphs of 1/(1+x)^(1/2), Summation to 160 terms, & Levin-U-transforms
Note how close equation, summation to 160 terms, and Levin-U-transforms are from -0.25 to 1.00
Note at x=1 the extraordinary level of accuracy for Levin-U-transform taking into account only 13 terms.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
Close up picture -0.25 to 1.0
Series to 160 terms [Green], and Levin-U-transforms [Red] are close together but do not match exactly the equation values [Blue].
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
have fixed it so your function works see |S1-s2|<0.003 use any accuracy you like here.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This does not work. The sum that I need is s[0]. You mixed it with s[3] which is my sum - f(x). Like you wrote LE(2) - F(2). It just means |0-0.577|=0.577.