Community Tip - Your Friends List is a way to easily have access to the community members that you interact with the most! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Catenary and cone - one fresh problem for Mathcad community
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Catenary and cone - one fresh problem for Mathcad community
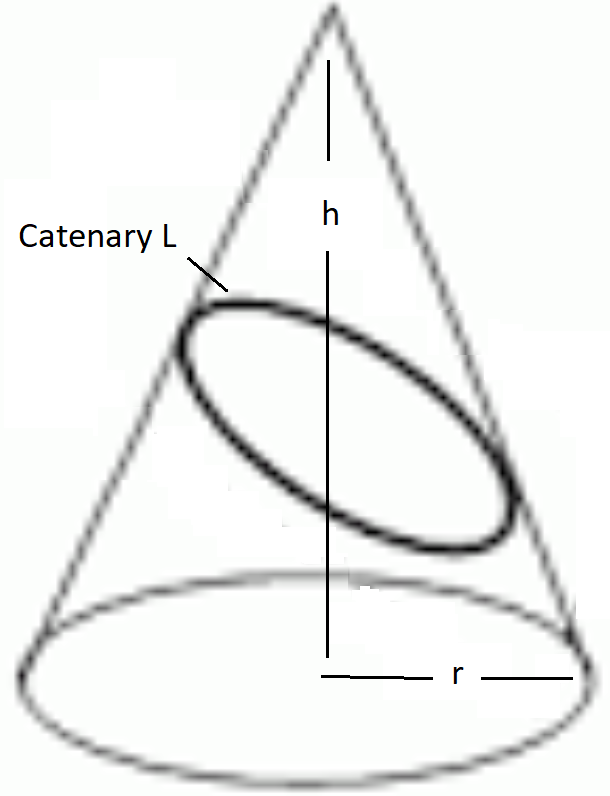
Do you know how a catenary lies on the cone? Without friction!
- Labels:
-
Algebra_Geometry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Valery,
You should be clearer because the figure shows an ellipsis. It is known to all that the intersection of a plane with a cone is a conic (in this case ellipsis precisely). Therefore I deduce that the catenary is generated by the intersection of a cone and a non-flat surface. the system between the equation of a cone and an unknown surface must give a catenary. Does this surface exist? ......but then, since the catenary is a flat curve, the surface should be a plane, which contradicts the previous deduction.
The cone is ready...........
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
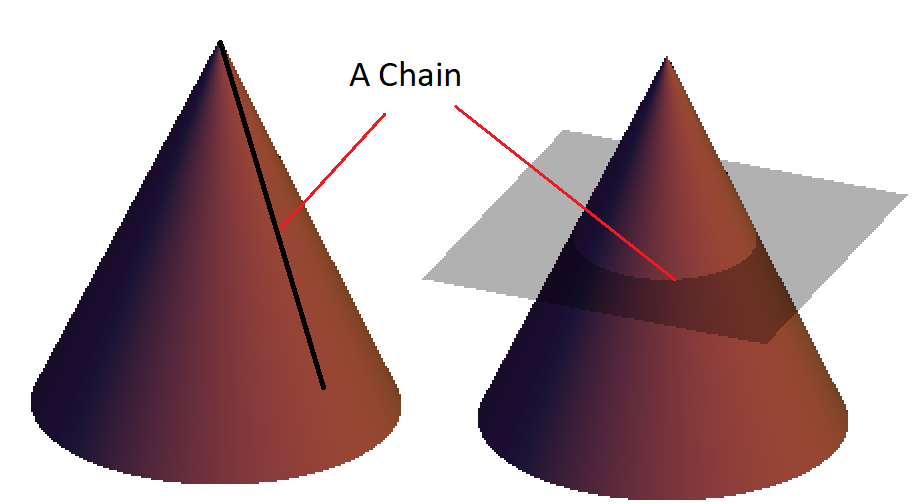
1. Sorry, it is not a catenary (one plane curve), but a chain.
2. Better use a cylindrical system of coordinates
3. This problem has two boundary cases:
- a circle
- a part line
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So the problem seems trivial because the circle is given by the intersection of the cone and a plane perpendicular to the axis of the cone, while the chain is the locus of points where the plane is tangent to the cone .....
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The basic catenary (chain suspended from each end) is constrained by requiring the horizontal component of tension be the same for each point along the curve.
This problem requires two additional constraints:
- the chain must lie on the surface of the cone, and
- the length of the chain, and the end points must be specified.
A general solution is going to be complicated.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi FredKohlhepp,
I fear that the chain suspended between the two ends is simply your "invention".
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@-MFra- wrote:
Hi FredKohlhepp,
I fear that the chain suspended between the two ends is simply your "invention".
What is your definition of "catenary"?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Fred_Kohlhepp wrote:
@-MFra- wrote:
Hi FredKohlhepp,
I fear that the chain suspended between the two ends is simply your "invention".
What is your definition of "catenary"?
Sorry - not a catenary but a chain, a round chain.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
Sorry - not a catenary but a chain, a round chain.
Okay, but you put catenary in the title; and the statement that it's a chain implies a condition about tension in the chain.
I'm not trying to invent anything, just make an observation about the problem. 🙂
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One auxiliary problem!
A round ideal chain is fixed without friction in/on/with two points.
We have one Unstable equilibria and two symmetric stable equilibria - see a picture.
Let solve this problem at first with Mathcad!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The chain is not elastic, it is inextensible like a rope. Quite right? In points 1 and 2 the chain flows freely and without friction, right? you desire the study of the motion of the system, assuming that there is no friction, and that on it acts the weight force only. The motion starts from any position. Quite right? Or should we also consider the rotary motion of the chain?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@-MFra- wrote:
The chain is not elastic, it is inextensible like a rope. Quite right?
Yes!
In points 1 and 2 the chain flows freely and without friction, right?
Yes
you desire the study of the motion of the system, assuming that there is no friction, and that on it acts the weight force only. The motion starts from any position. Quite right?
No!
Let start not with a dynamic but with one static problem!
It will be a good problem for students - to create an animation with D := L/2/999*FRAME - see please the picture above. At D=0 we have a vertical straight line segment. And at D->L/2 we have a horisontal straight line segment. Between those two boundary points we haw two catenary - a big and a small. This problem can be solved thru two ways - by Newton (forces) or by Lagrange (potential energy).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I am solving (try to solve with Mathcad) the problem from the article: