Challenging program, easy solution?

[ptc-5020731]

Hi everyone, I'm having some issues with a very large and complex program. I'm working with very little steps of time and I have to do more or less like 600.000 iterations to get a good result. The problem is that I'm working with matrices and at the end of the program I get results of the different variables wich are displacement, speed, acceleration and force in a vector that contains 3 components for each iteration that represents the displacements, speed... of 3 masses. I want to represent these results and I need to get for each step of time the result of the correspondent vector.

Actually the program does what I want (take it as an exmple of what I want to obtain) but in a very inneficient way, it trasnpose the big matrix and extracts each element of it, and creates a new vector with these elements, but it doesn't allow me to increase the numbers of iterarions needed to solve the problem because my computer runs out of memory in that step.

So, finally, please don't pay much attention on the rest of the code, (if you don't want) and please take into account what I've said. There has to be a way to get the elements of the matrices in some other more efficient way.

In summary. 1st don't be scared, there are only 2 things to check.

I need nf to be 600.000 (changing the number is easy, be able to get a result changing it, is the challenging part)

And change this part of the code, to make the same, but more efficiently.

THX in advance. Sorry for my grammar, spelling, etc. I'm not a native english speaker.

[Werner_E · Accepted solution]

Here is a much more efficient mkMat() routine. I knew that the built-in routine stack is much slower than if you program it yourself using for-loops, but I could not image how much slower it is - incredible.

Don't know how I could help with the problem of the number of iteration steps.

How do you know you need 600000 steps? Just because the result with 200000 is too inaccurate?

There is a problem with numerical iterations. If you take too few steps the result is inaccurate an not useable. But If you take to much steps it is possible that beacuse of cumulated rounding errors and other numerical inaccuracies the result gets unusable, too.

As of the out of memory problem: Would it be accaptable to store only every fifth or very tenth vector?

[ptc-5020731]

Let's say that you deserve a promotion and a rise.

I need 600.000 iterations because with each 100.000 I got 0.01 s of analysis, so 600.000 iterations 0.06 s of analysis. I need this kind of precision because the displacements of the masses are very small and the model needs to take into account this behaviour.

Again, Thank you very much, for the quick response and for the faster code.

[ptc-5020731]

Would it be accaptable to store only every fifth or very tenth vector?

I don't know, it seems that now the problem is not at the end, is that mathcad cannot handle more than 500.000 interations executing the main code.

Anyway, the result with 500.000 iterations is useful, but it would be perfect if I could make a million or 2 million.

Thx again.

[Werner_E]

The question would be if you really need ALL of the interim results. I understand that you need the 1 million steps for acurracy reasons, and calculating them would be just a matter of time, not of memory, I guess. Storing and returning all of those iteration steps is memory consuming. 1 million of steps would result in a return vector with a total of 12 million numbers - maybe too much.

So it depends on what you will be doing with the calculated data. Just for graphing you sure do not need 1 million points.

What I had in mind was that you do the iteration 1 million of times but you only store every tenth vector to stay within a memory limit.

[Werner_E]

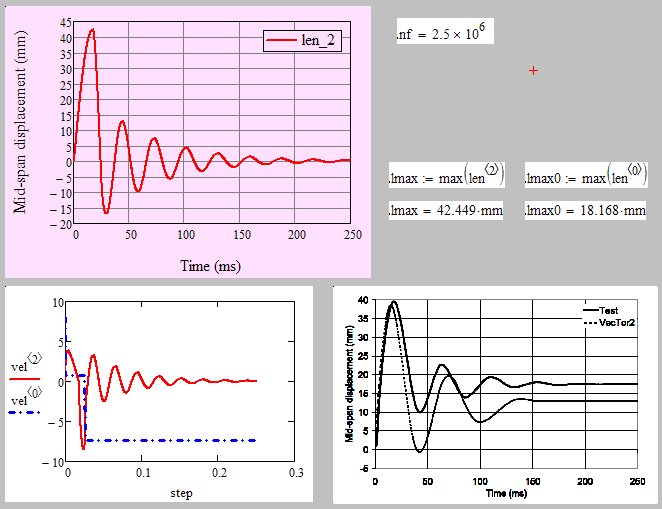
Here's your simulation with 2.5 millions iterations. In the file I take only every 1000th value and you can even change that to 10000 without much visible effect. The iteration itself is done 2.5 million times, so you lose no precision by omitting values.

Please check if I replaced all variables correctly (x[i --> x.old, x[i+1 --> x.new, etc.) The result looks pretty similar to the pic you provided apart from a slightly higher amplitude, a higher frequency and a smalller/slower damping, which may be due to different start values?. Its noticeable that the direct component/AC component/offset (whats the correct expression?) is not zero in your pic while in the graph of your file it is.

I added units for "len" and "step", you may do so with the other variables, too. And I used the units, labels and legend in the first graph as you have it in your pic.

[ptc-5020731]

As always an incredible good answer. I am very grateful for your work.

One question, why have you changed the names of the variables? I can change them as how they were named before?

Again. Thank you very much.

[Werner_E]

One question, why have you changed the names of the variables? I can change them as how they were named before?

Because the variables used for the iteration are no longer part of the resulting vectors, only every nn-th value is put in the vector. If you change them back from x.old to x[i, you will end up with too large matrices and wrong values. You may change x.old to x.i as literal index and x.new to x.i+1 (using the Ctrl-Shift-K trick), but I would find that too confusing and misleading and I see no reason for doing so.

In other words, the iteration is not done in and with th values of the result vectors but with a separate set of variables - "old" and "new". In the iteration step the "new" values are derived using the "old" ones and at the end of the iteration the "old" are overwritten by the "new" in preparation for the next iteration step. Only every nn-th value is taken for the output vectors.

I don't know what you intend to do with the output values other than using them for graphing, but I guess you don't need them all. Other wise you woul have to split the calculation into parts.