- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Changing display format of symbolic solution
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Changing display format of symbolic solution
Hello,
Can anybody tell me if there is a possibility to change format of equation solved symbolically?

I would like to get result such like a0/(1 * omega^2 - b0). How can i change coefficient standing by omega^2 to 1, for the rest to change adequately?
Second of all, thy does results differ, whether keywords are used one after another or used in batch?
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Like so?
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ok, but how about cases, when both nominator and denominator contains polinomial of n-th and m-th range? It was the simpliest example i had to solve, but there are more complex waiting ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Karol Niemczyk wrote:
Ok, but how about cases, when both nominator and denominator contains polinomial of n-th and m-th range? It was the simpliest example i had to solve, but there are more complex waiting
I guess you would define H(s) in terms of unassigned variables, and make fn a function of those that remain after the second-line calculation, so you can substitute numerical values for them. If you supply a more complicated H(s) we can try it.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Honestly i've been thinkig of making universal function to calculate it for any input values. But it doesn't work. It casts "Patern match exeption"

Btw. next transmitances are as follow:
1. (s^2 + 3.431) / (s^2 + 0.5778s + 0.5408)
2. (s^2 + 8.106) / (s^2 + 0.1831s + 1.033)
3. (0.008093 * s^4 + 0.09338 * s^2 + 0.2251) / (s^5 + 1.164 * s^4 + 1.986 * s^3 + 1.373 * s^2 + 0.8393 * s + 0.2251)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Try separating numerator and denominator and dividing both by multipliers of leading term in denominator then recombining. Example below (arbitrary values used):
However, your last three examples don't need this extra complication, they work using the same approach as my previous post.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Think Alan has already answered your main question.
As to the strange behaviour of the symbolic evaluation - this is due to the fact, that Mathcads symbolics (which isn't state of the art, anyway) switches to a very nasty floating point mode as soon as only one single decimal point is present in the expression. Outcome in this mode (while probably mathematically correct to a certain level of numeric accuracy) can be really bizzare, sometimes. So whenever possible try to avoid decimals (not always easy, I know) in conjunction to symbolic evaluation.
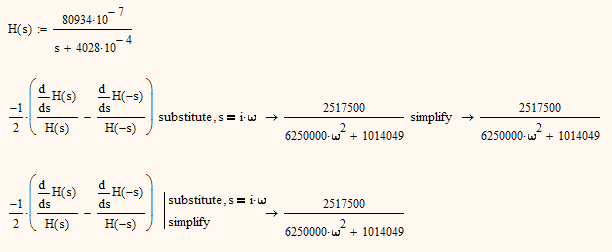
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks a lot. I'll keep this in mind. Nobody truly told me that before :S
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Alan,
This is earily similar (the work around with the denominator) to the work around in the insulation problem we went through a few months back
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
ELSID wrote:
Alan,
This is earily similar (the work around with the denominator) to the work around in the insulation problem we went through a few months back
Yes. Stay here long enough and you'll see the same things come up time and again. But that's a good thing because it means there are always new people getting involved.
Alan





