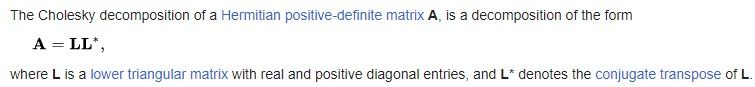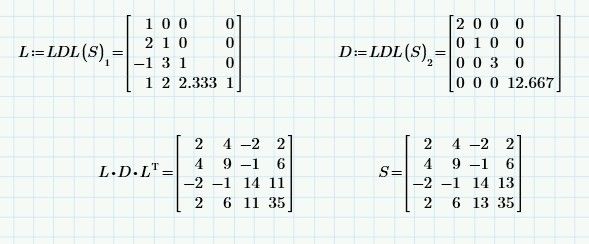Cholesky decomposition & the LDL decomposition. finding D?

[JBlackhole]

to all,

A question regarding the Cholesky LDL decomposition.

given a matrix A one can have A=LDL* where L* is the transpose of L

using the mathcad 15 cholesky(A), how does one code mathcad to get D?

L = cholesky(A)

Thanks in advance

Josh

[TH_10592087]

What D

Cheers

Terry

[TH_10592087]

LDL Decomposition is not available it would be necessary to program it.

•Cholesky—Cholesky square root of a matrix
•LU—LU factorization into lower and upper triangular matrices
•QR—QR factorization into an orthonormal and upper triangular matrix
•svd—Singular values decomposition

Solve a linear system of n equations in n unknowns using the lsolve function

[JBlackhole]

from the same source ...

[TH_10592087]

Hi,

Still necessary to program it

[Werner_E · Accepted solution]

The LDL decomposition is not Cholesky, rather a slight modification of it with the benefit of not having to take the roots.

But its very easy to get the LDL once you already have  the Cholesky decomposition:

You may now define a custom LDL function which does exactly these few steps

[JBlackhole]

Thanks a lot for that @Werner_E .

I was looking at pre & post multiplication ! Something like L^-1 A (L*)^-1. but you ends up with a "diagonal" matrix with unit value 

[Werner_E]

---

@JBlackhole wrote:

Thanks a lot for that @Werner_E .

I was looking at pre & post multiplication ! Something like L^-1 A (L*)^-1. but you ends up with a "diagonal" matrix with unit value 

---

If you mean by L the result of the cholesky function, this should  not be surprising. When the decomposition is S=L*L^T, then the only matrix you could squeeze in between using the very same L matrix is the identity matrix I -> S=L*I*L^T.

An additional advantage of the LDL* decomposition over Cholesky is, that it can also be used for indefinite matrices. But the approach I showed will of course not work ib that case because I am using the built-in cholesky() which will only work for positive definite matrices.
A more general LDL() function would have to be implemented in a different way without using cholesky().

[TH_10592087]

Hi,

Here is the LDL factorization.  If you want to extend this to the solution of Ax=b just ask.

Reference is: https://sites.ualberta.ca/~xzhuang/Math381/Lab5.pdf

Good Luck With It.

[TH_10592087]

Hi,

Revision to program to correct second summation.