Community Tip - Your Friends List is a way to easily have access to the community members that you interact with the most! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Cone surface as sum - why not correct?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Cone surface as sum - why not correct?
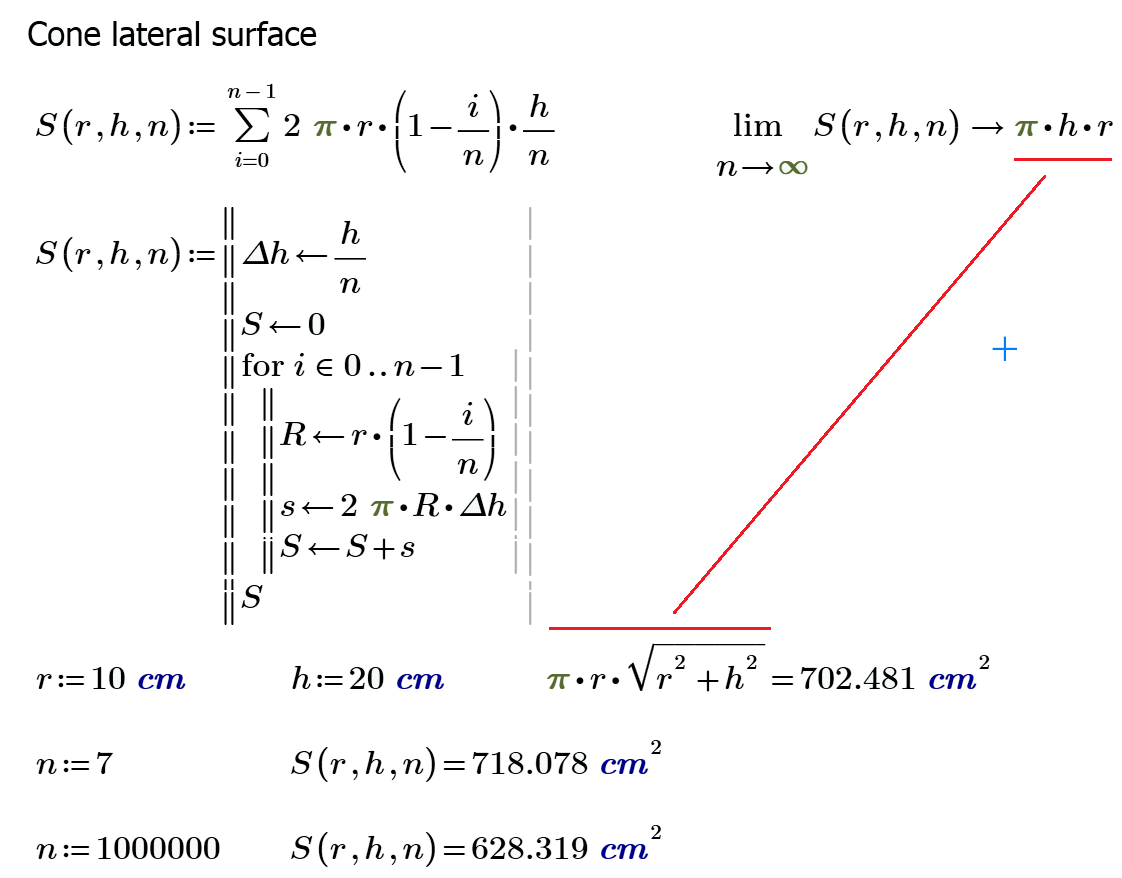
With volume all ok - http://communities.ptc.com/message/268582
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Your expression for S only adds up vertical heights, not slant heights.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Shouldn't that be equivalent, when going to the limit ?
Back to something more academic, to me, it is like the trapezoidal rule VS forward or backwards rectangle method: when going to the limit, shouldn't you end up with the same result ?
Damn, university was such a long time ago ...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlanStevens wrote:
Your expression for S only adds up vertical heights, not slant heights.
Alan
I feel it myself. But no slant too in the right case of the volume.
what is a correct limit?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
AlanStevens wrote:
Your expression for S only adds up vertical heights, not slant heights.
Alan
I feel it myself. But no slant too in the right case of the volume.
what is a correct limit?
Maybe like this:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Why would you do that ? If it is just changing the coefficient that bothers you with the right one, that's kind of cheating. What is your mathematical reason for doing so ?
It seems to me that what you are trying to do here is to pile up sections of a cone rather than cylinders. And you need the formula for the surface of a cone to do so. Which is what you are looking for. In French we say it's "a snake biting his own tail".
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I tried to have sqrt in answer of limit without sqrt in the origin model as we have 1/3 in answer of limit for volume of cone without 1/3 in the origin model.
In my childhood I asked why we have 1/3, not 1/2, 1/4 etc in the formula for cone volume.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Adrien Thurin wrote:
Why would you do that ?
For the same reason you do likewise when you derive the formula for the arclength of any curve or the formula for the surface of revolution ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
For the same reason you do likewise when you derive the formula for the arclength of any curve or the formula for the surface of revolution
OK, you got me ![]() In my defense, I don't remember ever studying that...
In my defense, I don't remember ever studying that...
Just when I was typing an answer, after a passionate discussion with a colleague about that...
Basically, there is no reason to only consider the lateral surface of the cylinders that are piled up in your sum. If you are looking at the lateral surface, you should consider the "visible top surface" of each cylinder, which is Pi * ((R * i)^2 - (R * (i-1))^2). And you end up, again, with a wrong result when you go to the limit ( Pi * r (r + h) ).
So basically, what you end up trying to do is trying to approximate the hypotenuse of a triangle with one of its sides, which obviously won't give you the right result. Clearly, there is no way around it, you have to consider the hypotenuse of the triangle, not just one side (R), nore the sum of the sides (R + H).
So in conclusion, this way of calculating the surface is just not valid. You just have to approximate each bit by something with a slope, not just flat ends.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So basically, what you end up trying to do is trying to approximate the hypotenuse of a triangle with one of its sides, which obviously won't give you the right result. Clearly, there is no way around it, you have to consider the hypotenuse of the triangle, not just one side (R), nore the sum of the sides (R + H).
Thats not equal but very similar to the approach of approximating the diagonal of a square by steps which are getting smaller and smaller. The optics looks like the step is appraoching the diagonal, but if you look closer you see that neither the full sum of all horizontal and vertical line segments nor the sum of the horizontal segments only will give you any approximation of the square root of 2. The first sum will always be 2 and second always 1.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
That's exactly what I meant, but expressed in a much much better and understandable way ![]()
Thanks Werner !
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It will be good to show on this animation how change or not the length of this curve!
Werner!
Can you create an animation for this group
http://communities.ptc.com/groups/animation-of-math-methods-in-mathcad
A set of cylinders with different R (a children toy pyramid) goes to the cone: what is the current V and S of this body at different n.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It will be good to show on this animation how change or not the length of this curve!
That won't be that spectacular and I guess its fairly obvious that the curve length is constant 2.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator


