Cone surface as sum - why not correct?

[ValeryOchkov]

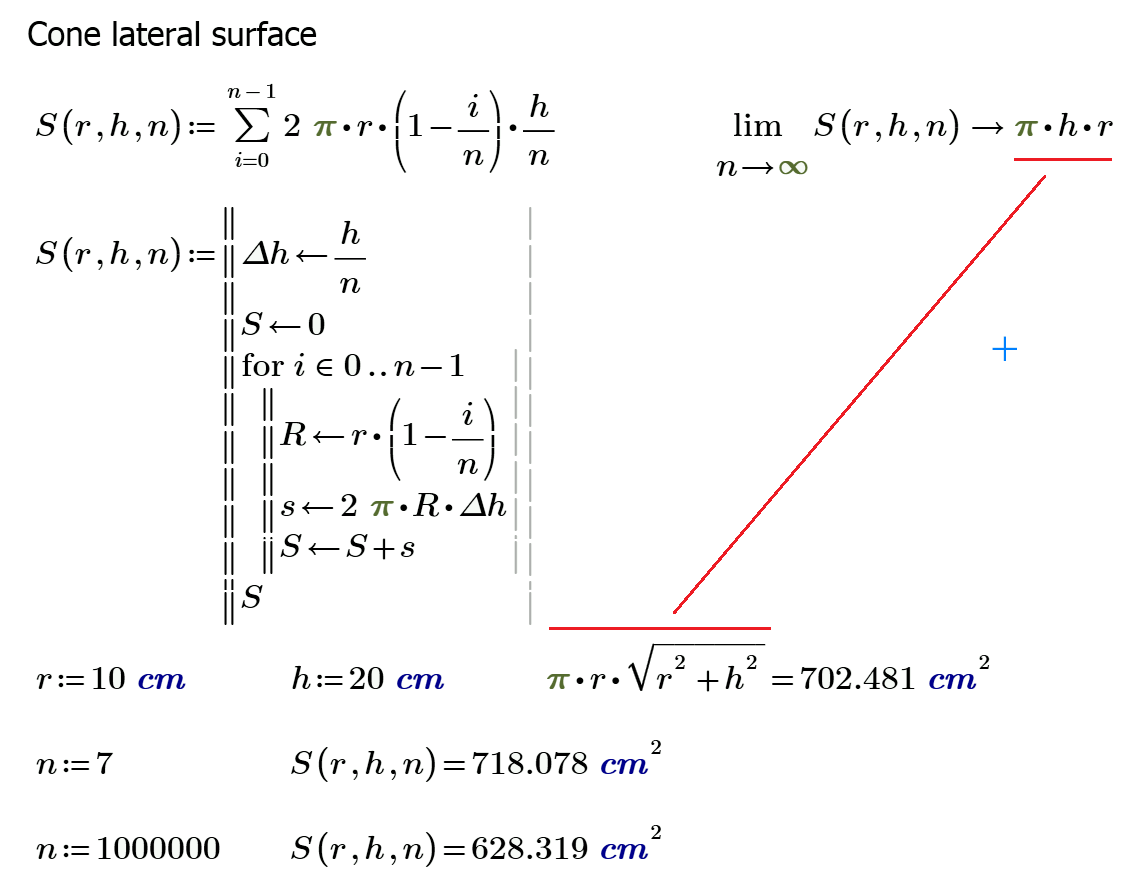
With volume all ok - http://communities.ptc.com/message/268582

[AlanStevens]

Your expression for S only adds up vertical heights, not slant heights.

Alan

[athurin]

Shouldn't that be equivalent, when going to the limit ?

Back to something more academic, to me, it is like the trapezoidal rule VS forward or backwards rectangle method: when going to the limit, shouldn't you end up with the same result ?

Damn, university was such a long time ago ...

[ValeryOchkov]

AlanStevens wrote:

Your expression for S only adds up vertical heights, not slant heights.

Alan

I feel it myself. But no slant too in the right case of the volume.

what is a correct limit?

[Werner_E]

Valery Ochkov wrote:

AlanStevens wrote:

Your expression for S only adds up vertical heights, not slant heights.

Alan

I feel it myself. But no slant too in the right case of the volume.

what is a correct limit?

Maybe like this:

[athurin]

Why would you do that ? If it is just changing the coefficient that bothers you with the right one, that's kind of cheating. What is your mathematical reason for doing so ?

It seems to me that what you are trying to do here is to pile up sections of a cone rather than cylinders. And you need the formula for the surface of a cone to do so. Which is what you are looking for. In French we say it's "a snake biting his own tail".

[ValeryOchkov]

I tried to have sqrt in answer of limit without sqrt in the origin model as we have 1/3 in answer of limit for volume of cone without 1/3 in the origin model.

In my childhood I asked why we have 1/3, not 1/2, 1/4 etc in the formula for cone volume.

[Werner_E]

Adrien Thurin wrote:

Why would you do that ?

For the same reason you do likewise when you derive the formula for the arclength of any curve or the formula for the surface of revolution

http://mathworld.wolfram.com/SurfaceofRevolution.html

http://en.wikipedia.org/wiki/Surface_of_revolution

[athurin]

Werner Exinger wrote:

For the same reason you do likewise when you derive the formula for the arclength of any curve or the formula for the surface of revolution

http://mathworld.wolfram.com/SurfaceofRevolution.html

http://en.wikipedia.org/wiki/Surface_of_revolution

OK, you got me In my defense, I don't remember ever studying that...

Just when I was typing an answer, after a passionate discussion with a colleague about that...

Basically, there is no reason to only consider the lateral surface of the cylinders that are piled up in your sum. If you are looking at the lateral surface, you should consider the "visible top surface" of each cylinder, which is Pi * ((R * i)^2 - (R * (i-1))^2). And you end up, again, with a wrong result when you go to the limit ( Pi * r (r + h) ).

So basically, what you end up trying to do is trying to approximate the hypotenuse of a triangle with one of its sides, which obviously won't give you the right result. Clearly, there is no way around it, you have to consider the hypotenuse of the triangle, not just one side (R), nore the sum of the sides (R + H).

So in conclusion, this way of calculating the surface is just not valid. You just have to approximate each bit by something with a slope, not just flat ends.

[Werner_E]

So basically, what you end up trying to do is trying to approximate the hypotenuse of a triangle with one of its sides, which obviously won't give you the right result. Clearly, there is no way around it, you have to consider the hypotenuse of the triangle, not just one side (R), nore the sum of the sides (R + H).

Thats not equal but very similar to the approach of approximating the diagonal of a square by steps which are getting smaller and smaller. The optics looks like the step is appraoching the diagonal, but if you look closer you see that neither the full sum of all horizontal and vertical line segments nor the sum of the horizontal segments only will give you any approximation of the square root of 2. The first sum will always be 2 and second always 1.

Video Link : 5583

[athurin]

That's exactly what I meant, but expressed in a much much better and understandable way

Thanks Werner !

[ValeryOchkov]

It will be good to show on this animation how change or not the length of this curve!

Werner!

Can you create an animation for this group

http://communities.ptc.com/groups/animation-of-math-methods-in-mathcad

A set of cylinders with different R (a children toy pyramid) goes to the cone: what is the current V and S of this body at different n.

[Werner_E]

It will be good to show on this animation how change or not the length of this curve!

That won't be that spectacular and I guess its fairly obvious that the curve length is constant 2.

[Fred_Kohlhepp]

you have to add in the slant!