Community Tip - Did you know you can set a signature that will be added to all your posts? Set it here! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Create and array of functions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Create and array of functions
Hello all,
My first post, I've used mathcad for pretty basic things till recently. Is there a way to use a for or while look to create an array of functions where the functions are dependent on the previous element within the array? This assume we define the first element of course.
an example would be f(x)=[2x, (2x)+1, ((2x)+1)+2, (((2x)+1)+2)+3, ...(nest)+n)]
Ideally f(#)[index would call the correct index: f(2)[0= 4.... and f(2)[3=10
Hope that make sense,
Sami
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
LucMeekes wrote:
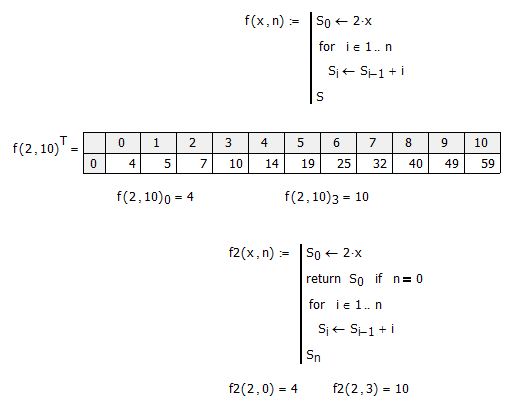
The short answer is: no, not exactly the way you describe. The problem is that you cannot grasp the index of an array element inside the definition of the array.
But you can get close. Up to you to decide whether that's close enough. See:
Now, to become independent of a definition of n (the size of the function array), we have to provide it as a parameter:
We can extend it a little bit further by including the initial function and the 'nesting' function as parameters ...

Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
What you are asking for does not create an array of functions. It creates an array of numbers. That's possible, but it's very inefficient to calculate an array of numbers up to some arbitrary limit, and then only return one of them. The second function gives the same answer, but only calculates what is necessary.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello,
Thanks for the response. I didn't quite explain myself well enough. I need the incidences within the array to remain a function of X so i can take the improper integral from 0 to inf of the last index. The function is a bit more complex that 2x but I just wanted a general form. The real function I am looking to create uses:
Where ϵr is an array of complex numbers, h is an array of real numbers, and beta is the variable to be integrated. In the real case I actually define the last element in the array as:
and will take the improper integral of the first index (backwards to the original post). I only suggested using a for loop and an array of functions cause I am new to mathcad and didn't see a more appropriate way. Definitely open to a better approach!
Sorry for the confusion but thanks for the help!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The short answer is: no, not exactly the way you describe. The problem is that you cannot grasp the index of an array element inside the definition of the array.
But you can get close. Up to you to decide whether that's close enough. See:

Now, to become independent of a definition of n (the size of the function array), we have to provide it as a parameter:

Hope this helps.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello,
Thanks for the help! This may work. In the end I need to take the integral of the final index, so if i can stick f(x,#) into an integral, it should work. I will give it a try!
Thanks a bunch!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
LucMeekes wrote:
The short answer is: no, not exactly the way you describe. The problem is that you cannot grasp the index of an array element inside the definition of the array.
But you can get close. Up to you to decide whether that's close enough. See:
Now, to become independent of a definition of n (the size of the function array), we have to provide it as a parameter:
We can extend it a little bit further by including the initial function and the 'nesting' function as parameters ...

Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Stuart,
I tried that as well. Found that it didn't work all the way through with numeric processing as you appeared to have found out as well. Asking for the result:
f(2)[3=
results in an error.
By the way. Integrals can also be used, up to a point:

But with:
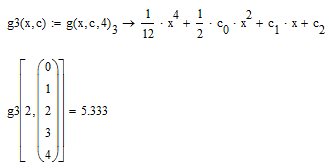
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Wish I could mark you all as correct but the site only lets me click one. Thank you all, most helpful indeed!
Epison and h are vectors with other constants





