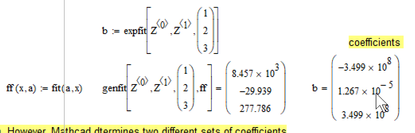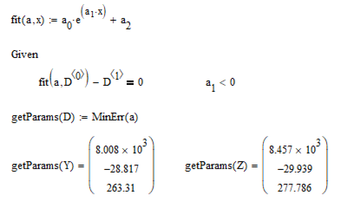Skip to main content
R
Raiko17-Peridot
17-Peridot
April 25, 2018
Solved

Data fit problem

  • April 25, 2018
  • 3 replies
  • 4076 views

Hello folks,

 

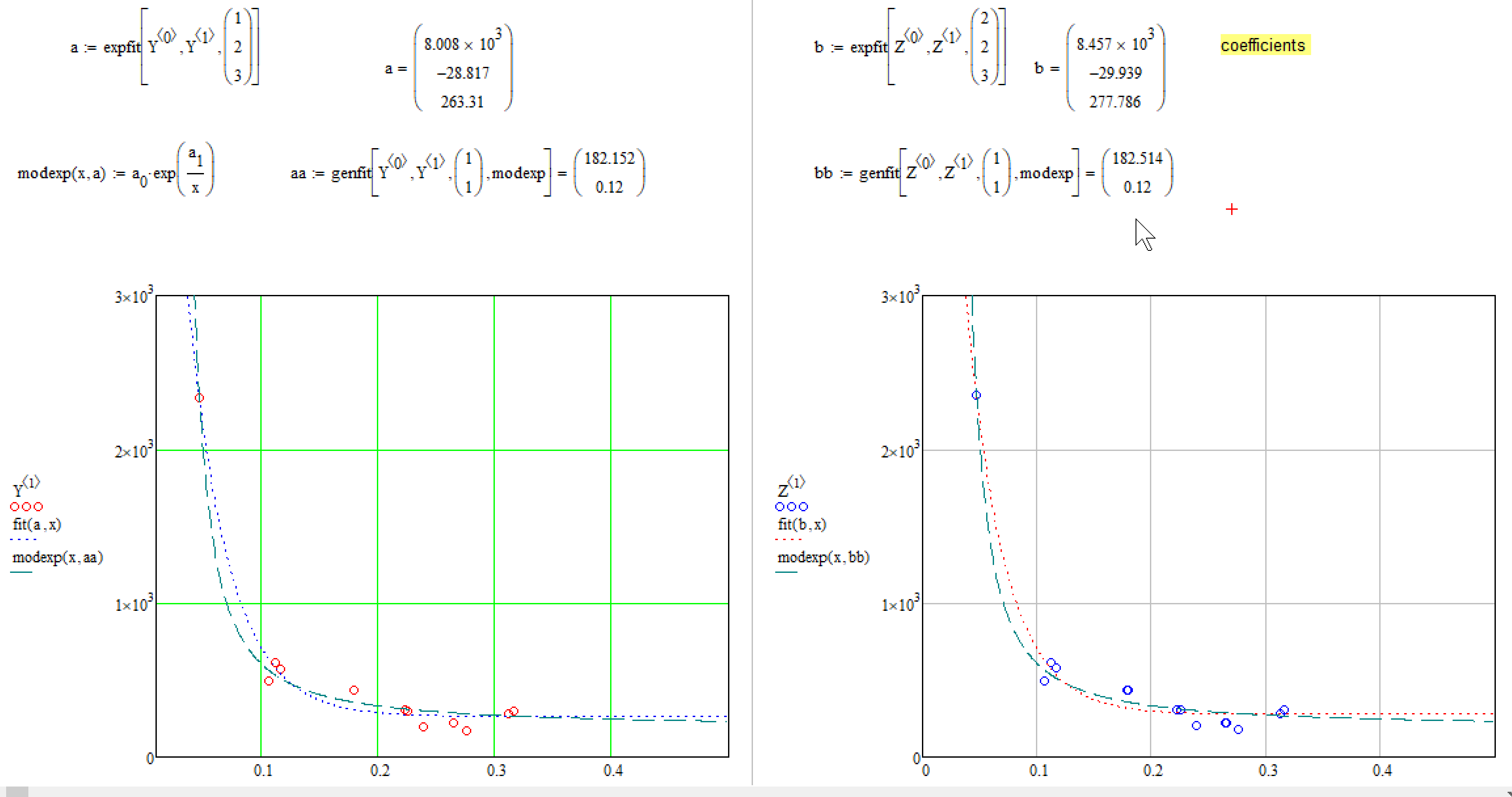
I'm currently doing data fits in a bulk; i.e. several hundred sets. Therefore, I'd like to automate this. Some data sets seemed peculiar and I noticed an odd behaviour when it comes to exponential fitting; see attached file.

In two different data sets, which are very similar, Mathcad's expfit function determines vastly different coefficients. Does any body has a remedy for this or can explain it?

 

I'm using MC15 on a 64 bit Win 7 machine.

Thanks

Raiko

Best answer by Werner_E

I think the conclusion so far is that you are better off using genfit or a solve block as opposed to expfit or you may fiddle around with the guesses.

I don't know if this would be an option but it looks to me that a modified exponential f(x)=a*exp(b/x) might make an equal good if not even a better fit and is only dependent on two parameters (BTW, as you can see in the pic, even changing the guess 1 to 2 makes expfit work OK):

B.png

3 replies

W
Werner_E25-Diamond I
25-Diamond I
April 25, 2018

I have no explanation (other than we are dealing with a numerical algorithm trying to fins a local(!!) minimum and so depends on the guess values) so but of course you can change the behaviour by changing the guess vector. Replace the 1 there for a 10(even 2 dows the job) and your second example gives you the result you expect.

Exchange the 1 for 0.1 in the the first example and it will give you the same undesired result.

I understand thats its quite demanding how to generate appropriate guesses in a bulk processing.

You may provide a few different guesses and calculate the Error (least squares) for the fit you get with each of them and then keep the best.

I also noticed that genfit seems to do a better job (at least with your second example).

B.png

Maybe a solve block with minerr does even better. At least you get the error immediately by evaluating the system variable ERR after the solve block.

F
Fred_Kohlhepp23-Emerald I
23-Emerald I
April 25, 2018

If you build a solve block, you can force the exponent to be negative.  may be enough. . .

W
Werner_E25-Diamond I
25-Diamond I
April 25, 2018

Time for some more coffee 😉

You have put the <0 in the index but the solve block gives the desired result even without this constraint (as does genfit). Looks like expfit is in some way too sensitive wrt guesses.

    F
    Fred_Kohlhepp23-Emerald I
    23-Emerald I
    April 25, 2018
    @Werner_E wrote:

    Time for some more coffee 😉

    No, I think it's time to retire!

    W
    Werner_E25-Diamond IAnswer
    25-Diamond I
    April 25, 2018

    I think the conclusion so far is that you are better off using genfit or a solve block as opposed to expfit or you may fiddle around with the guesses.

    I don't know if this would be an option but it looks to me that a modified exponential f(x)=a*exp(b/x) might make an equal good if not even a better fit and is only dependent on two parameters (BTW, as you can see in the pic, even changing the guess 1 to 2 makes expfit work OK):

    B.png

      F
      Fred_Kohlhepp23-Emerald I
      23-Emerald I
      April 25, 2018

      Just to justify my coffee consumption, I've modified the attached file from the previous blunder. 

       

      One thing to note:  change the TOL definition off and on, watch the results change!

      W
      Werner_E25-Diamond I
      25-Diamond I
      April 25, 2018

      Interesting observation - so the solve block is affected by TOL but expfit seems to be not.

      I don't think that you should abandon you solve block - it might be that the constraint a[1 < 0 can be necessary for other data sets.

      I am not sure if it better to use minerr (for which I have a tendency to) or minerr as you did. The results are marginally different and minerr seems not to be dependent on TOL.

      For the two datasets given the constraint a[1<0 would not be necessary and if I change that to a[1 > 0 is has no effect at all ? 😞

      B.png

      Terms & ConditionsCookie settingsAccessibility statement