Community Tip - You can change your system assigned username to something more personal in your community settings. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Debate on definition of arccotangent (acot)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Debate on definition of arccotangent (acot)
Hi all,
I just read an interesting post on two different intepretations of arccotangent. The author, some calculus textbooks, Mathcad and Maple interpret acot as
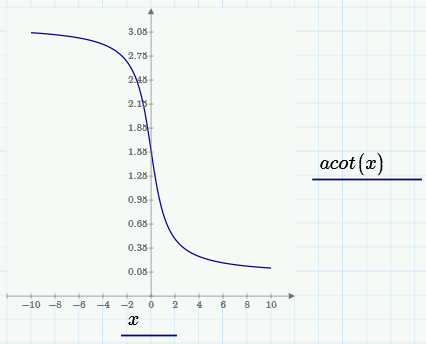
With the range defined as being between 0 and π.
However, Mathematica, Matlab, and some other calculus textbooks define arccotangent differently.
See http://www.squarecirclez.com/blog/which-is-the-correct-graph-of-arccot-x/6009 for the discussion.
What do you think?
Mona
- Labels:
-
Calculus_Derivatives
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
They are both valid answers (one of the comments makes this point). The function cot(x) does not have an inverse, because for any value of cot(x) there are multiple possible values of x (an infinite number of them in fact). To create an invertible function the domain of cot(x) therefore has to be restricted, and what acot(x) then looks like depends on the domain you choose. Apart from those two domains there are an infinite number of other possible choices. What constitutes the best domain depends on what you are trying to do. Generally, I think the Mathcad choice is the better one because the function is continuous and defined at 0. The Mupad implementation is discontinuous at x=0, and so (IMHO) acot(0) should be undefined. If you evaluate acot(0) symbolically what you actually get is pi/2 though, which to me seems inconsistent with the definition. At a minimum, it's an arbitrary choice, and -pi/2 would be equally valid.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Using Abramowitz & Stegun, the -π/2 to +π/2 seems to be the preferred option based on the integral formulation of arctan (arccot(z) being arctan(1/z) (and is the one chosen by the symbolic processor).
However, backward compatibility suggests keeping the current 0 to 2π and modifying the symbolic processor interface to make it return the 'correct' value and be consistent with the Maple result produced by M11.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is a definition from trigonometry:
![]()
The authors note that they elected to use intervals that match their reciprocal functions, except for one missing point.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think it will be better to show acot function ()and others trig) in polar graph - see:
http://twt.mpei.ac.ru/MCS/Worksheets/FMC/acot.xmcd
and a picture

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I discovered an anomaly for calculating lim arccot(x) when x-----> - infinite (minus infinite)
The right answer is of course "pi"
Mathcad 13 gives the right answer
But Mathcad 15 gives 0 (zero) as result !!
Has somebody met the same problem ?
Richard
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Read the thread above, and also the web page Mona links to in her post. Both answers are valid; it just depends on how you define acot(x).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I discovered an anomaly for calculating lim arccot(x) when x-----> - infinite (minus infinite)
The right answer is of course "pi"
Mathcad 13 gives the right answer
But Mathcad 15 gives 0 (zero) as result !!
Has somebody met the same problem ?
Richard





