- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Defining Weibull and custom function when using MonteCarlo
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Defining Weibull and custom function when using MonteCarlo
We have recently started on the more advanced statistical features in Mathcad. We would like some advice.
Using Montecarlo to generate random data we would like to use the Weibull distribution and then later a custom function for our calculations. However, we are experiencing some problems which we believe is due to our lack of experience.
The first issue is that specifying different Weibull parameters when used in a Montecarlo does not seem to change the shape of the graph (see Cylinder Radius on Pg 4). The red trend was generated using MonteCarlo with a shape factor equal to 1 defined in the seond column of the Rvals matrix on Pg 3. Changing this value however does not change the shape of the graph away from exponential decay as would normally be expected with the Weibull.
Are we defiing the parameters incorrectly or how do you change the shape for different shape factors inside the Rvals matrix.
The second issue we have is to define a customized distribution function in the dist matrix. As mentioned we woudl like to use the triangular or CuDist (Pg 1) distribution. However, we are struggling to define the limits. Using the Triang distribution we only get the average in the histogram (Pg 4) and not the triangular distribution expected as calculated on Pg 2.
Can anyone help please
Barend
- Labels:
-
Statistics_Analysis
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Barend,
I'm not actually sure what you're trying to do yet, but a quick check on your worksheet seems to indicate that the Weibull shape factor does have an effect and gives me the shapes I'd expect from that distribution.
Cheers,
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
We managed to simulate the Weibull as well. No problem. The problem is when trying to force the Weibull or a custom function in the MonteCarlo, then it does not work as expected (see our model). We would like to understand how to apply the MonteCarlo for this. As per Alan's reply it seems as if the built-in MonteCarlo does have its issues.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think the in-built montecarlo function is awkward and inflexible. I prefer to write my own routine. See attached for a couple of simple examples: one using a triangular distribution and the other using a three-parameter Weibull.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If we understand correctly, you therefore say that you do not use the MathCad built-in MonteCarlo at all, but generate your own random data according to your distribution. This means that the built-in feature is actually not a feature. The internal MonteCarlo seems to be much faster though, but then it seems limited in its application.
Are we understanding correctly. Speed is an issue as we are also applying it in more complex application where we have 20 variables. Running your model for 10000 iterations takes 100 seconds. Running our built-in model calculates almost immediately. True, we only have two variables where you have three, but the time seems hugely different. Is there any recommendation for speeding this up.
From experience, when you run complex models, what would the best hardware configuration be.
Barend
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Our guy looked at you model again and it might be the integral in the inverse distribution calculation might be the cause to the time increase. He is currently looking at 'n more direct comparison.
Barend
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Barend Botha wrote:
Our guy looked at you model again and it might be the integral in the inverse distribution calculation might be the cause to the time increase. He is currently looking at 'n more direct comparison.
Barend
Yes, this is exactly the reason my triangular distribution calculation is slow. The Weibull one is much quicker (and indeed could be made quicker still, as it is possible to get a direct inversion, rather than using the solve block to invert it). I'm sure there are ways of speeding up the inversion process (see attached for a much quicker triangular version), but my aim was simply to show that Monte-Carlo is more flexible and more under your own control, if you don't use the built-in function (which was only added in MC15). Also, I defined the cdfs myself, but you could use the in-built ones, if they meet your needs (there's nothing wrong with them - I don't think there's a triangular one though.)
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks. Understood. The problem now still comes back as to waht we are doing wrong trying to apply the Wiebull. The normal and lognormal is fine, but the Weibull built-in seems to be beating us. I like the Weibull as it covers a number of other distributions greatly removing the need for custom functions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Obviously montecarlo() is poorly documented, to say the least. I never used it and just played around with it and it seems that the functions you provide in your dist vector are supposed to accept one (dummy) argument and should return a single random value. The argument of Weibull() and Normal() is the length of the vector of random numbers returned, but if the parameter is 1, a single scalar (not a 1x1 matrix) is returned. Weibull(), according to help, is only using shape=1.
To use a Weibull or any other user defined distribution it looks like it had to be written to accept 1 argument and return a single scalar random result. So to use Weibull with a different shape you define a new function using rweibull(any,shape) and take the first element of the vector this function returns. rweibull() will return a 1x1 matrix if the first argument is 1.
See attached.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It can also be convenient to use local function definitions in the argument placeholder.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It seems that I am missing the point.
The benefit of the method you showed compared to that shown below is, that f() in your version must not know anything about the number of arguments in g3 ??
How would that thelp in defining the distribution function for montecarlo()?
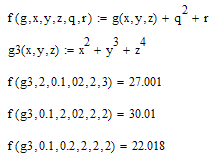
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner
To confirm that we used your approach and then also defined an inverse function for the traingular distributions and it now seems to be working. Attached the example.
Thanks a lot for the assistance.
Barend
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So I guess my interpretation of how the function inserted should be structured was corrct. Its a pity that montecarlo() is so poorly documented.
Nevertheless I would second what Alan had written - you have better control with self written routines.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Barend Botha wrote:
... The normal and lognormal is fine, but the Weibull built-in seems to be beating us....
Not sure if it's the in-built Weibull per se that is beating you, or its use in the in-built MonteCarlo function.
If the former, the attached might help.
Alan





