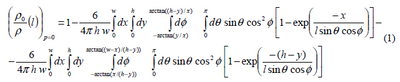Community Tip - New to the community? Learn how to post a question and get help from PTC and industry experts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Definite 4D integral evaluation (Fuchs-Sondheimer Resistivity model for Nanowires)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Definite 4D integral evaluation (Fuchs-Sondheimer Resistivity model for Nanowires)
Hello,
I really appreciate it if someone can help me to double check the following equation by running my sheet in their Mathcad. I attached my sheet.
This time, I use different formula from my previous post here.
In the mean time, I am writing matlab code to double check as well.
I run my sheet, it took so much time with my pc and at the end it show error.
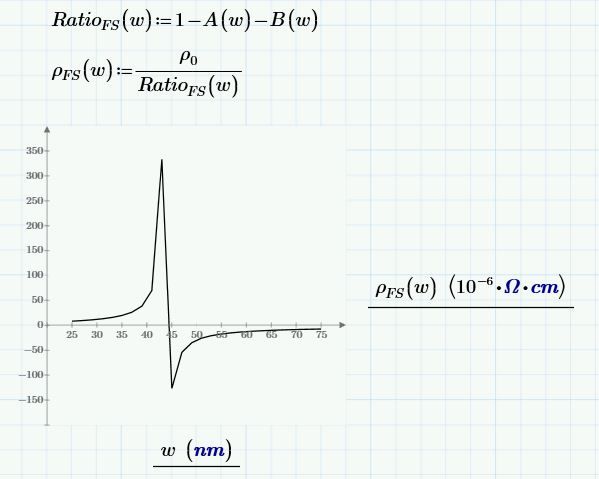
The formula to compute:
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
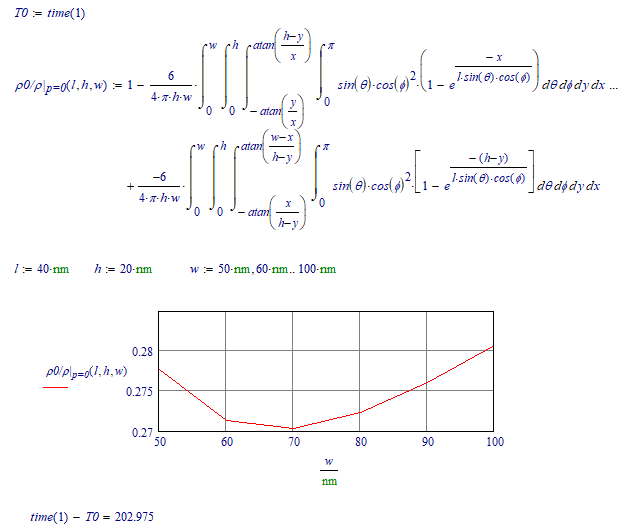
And YES, there are ways to speed it up.
This is the time to calculate 6 points on my pc:
If you notice that the integrand function to dTheta is symmetric around pi/2, we can omit half of the integration:
Down from 203 to 92 seconds.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
You need to be very patient for a result
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@terryhendicott
hi...thank you.
could you run it once again from w: 20-70 nm?
The motivation is to see the w around lambda and thickness h.
I tried in my pc from w: 25 - 50 nm. it still takes long time.
is there tips to speed up the calculation?
I use ORIGIN=0, TOL=10^-3, CTOL=10^-3
@LucMeekes
Hi..yes, the integral notation confused me.
But after reading the very original paper, which use such a notation, nested integration is my conclusion.
In your sheet, your third term uses +, it should be -.
You might got that from the paper, which shows double minus sign.
Thank again for your help.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
Cheers Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The third term is negative, due to the -6 that it starts with. If used the expression continuation (continues the expression from the previous line). In Mathcad that is only possible with an addition, so I just add a negative expression...
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And YES, there are ways to speed it up.
This is the time to calculate 6 points on my pc:
If you notice that the integrand function to dTheta is symmetric around pi/2, we can omit half of the integration:
Down from 203 to 92 seconds.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
deleted
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
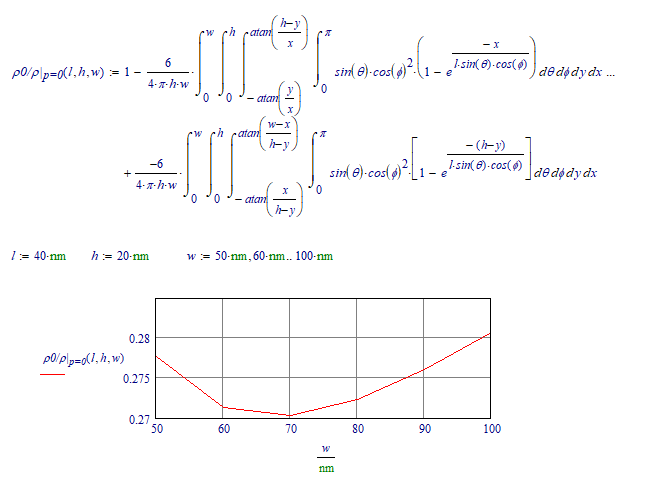
Assuming that weird integral notation actually is intended to mean the nested integrals below:...
Success!
Luc
P.S. It also means that the expression in your other thread was actually meant to be a nested integral, rather than a product of integration results. That other expression easily runs into overflows when trying to (numerically) integrate. No symbolic solution was found.