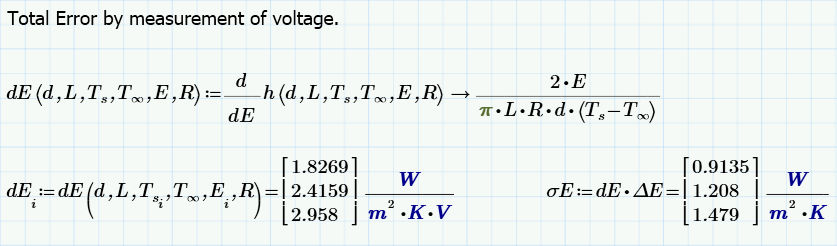Community Tip - If community subscription notifications are filling up your inbox you can set up a daily digest and get all your notifications in a single email. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Derivative a scalar
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Derivative a scalar
Hello.
I'm trying to derive a formula which is a function of six values. Four of them are just constants but the other two are vectors of three values.
d = constant
L = constant
T = [T1, T2, T3]
T_inf = constant
E = [E1, E2, E3]
R = constant
I want to get three values from the dT_i. Thanks..

Solved! Go to Solution.
- Labels:
-
Calculus_Derivatives
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You can't take the derivative w.r.t a subscripted variable, or a variable that is a vector. The easiest solution is to first create a function, and then apply that to the vector variable.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It's hard to debug a picture. Try using the vectorize operator over the derivative of the function. If that doesn't work, please post the worksheet.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello Richard.
Thanks for your reply. I couldn't figure this out so here is the file.
I hope someone can help.
BTW. I'm sorry for posting in wrong section. Though I was located in the "Calculus & Derivatives" when posted.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You can't take the derivative w.r.t a subscripted variable, or a variable that is a vector. The easiest solution is to first create a function, and then apply that to the vector variable.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I can't open the file but I tried that and it works perfectly.
Thanks.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It was created in Prime 3.0. Are you using an earlier version? If so, you should state that in any future questions. Prime 3.0 can't save back to earlier versions, but I would have posted a picture.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'm sorry. I should've mentioned my version. I'm using Prime 2.0.
But deriving the equation before giving the values does the trick. ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Please find a PDF and XPS version of this worksheet in attachment.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for the pdf. It's not like what my solution was.
But this doesn't work for me... MathCAD says it doesn't recognise the values. 😕
It shows error on d, but it is also on the other values.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Delete the inline evaluation on the right hand side of the function definition.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Doh, I can't belive I didn't notice that. Thanks!
Now everything works like it should.
Instead of he evaluation on the right I use -> to see the derived equation.