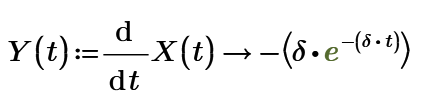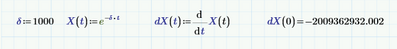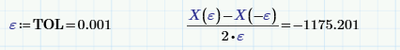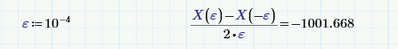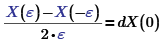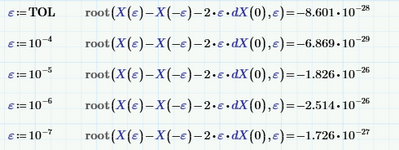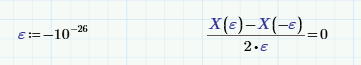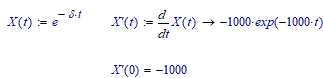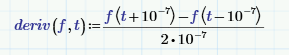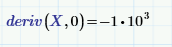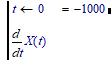Skip to main content
A
Anonymous
March 28, 2022
Question

Derivative calculated incorrectly

  • March 28, 2022
  • 4 replies
  • 2642 views

I really don't understand why when using a Symbolic Calculation, the value is obtained more accurately than when checking the value normally. What should I do so that the derivative is calculated correctly?

 

KULBE_0-1648507916938.png

 

 

4 replies

P
ppal_25568718-Opal
18-Opal
March 28, 2022

Looks like a bug! Seems to diverge after delta = 287

 

 

ttokoro
21-Topaz I
ttokoro21-Topaz I
21-Topaz I
March 28, 2022

I think its a bug. Use next Tip.

image.png

t.t.
L
LucMeekes23-Emerald IV
23-Emerald IV
March 30, 2022

You should realise that the numeric and symbolic processors in Mathcad and Prime tackle mathematical problems differently, and sometimes that leads to different results.

So we have (also in Prime 4):

LucMeekes_0-1648633971811.png

And this is clearly a bug, because the answer should be -1000 exactly. Assuming that the numeric derivatie would be calculated with:

LucMeekes_1-1648634022281.png

Setting a reasonable value of epsilon, like TOL, gives:

LucMeekes_3-1648634360847.png

That's closer, but not good. Try:

LucMeekes_4-1648634392363.png

Hmm:

LucMeekes_8-1648634823228.png

Now we're getting somewhere.

We can try to find the value of epsilon that Prime would use, if my assumption is correct, with:

LucMeekes_5-1648634495481.png

Working that around, and using the root function gives, for various guess values of epsilon:

LucMeekes_6-1648634558361.png

OK, let's try:

LucMeekes_7-1648634659316.png

Apparently Prime uses a different, buggier method to numerically find the derivative.

 

So, in case of numerical derivatives, you should better define the derivative yourself, using the symbolics:

LucMeekes_9-1648635416046.png

Or you can check the numerical derivative with:

LucMeekes_10-1648635463445.png

Which gives:

LucMeekes_11-1648635491907.png

for your example.

 

Success!
Luc

 

 

 

    W
    Werner_E25-Diamond I
    25-Diamond I
    March 30, 2022

    Apparently Prime uses a different, buggier method to numerically find the derivative.

     

    Not only Prime, the problem already exists in real Mathcad. Here is a screenshot from MC15

    Werner_E_1-1648638360599.png

    Also interesting and confusing that for values between 2350 and 3600 the algorithm returns the correct result just to fall back to 0 for larger values of delta.

    What does it look like in MC11?

    Worksheet in MC11 format attached

     

    BTW, as far as I know Mathcads numeric algorithms often followed the ones found in the "Numerical Recipes" (http://numerical.recipes/). Not sure if this would also apply to the numerical derivative. Chapter 5.7 dealing with numerical derivatives can also be found here http://pelusa.fis.cinvestav.mx/tmatos/LaSumA/LaSumA2_archivos/NumeRCPs/Texto/bookcpdf/c5-7.pdf

    Interesting to read anyway.

    L
    LucMeekes23-Emerald IV
    23-Emerald IV
    March 30, 2022

    Mathcad 11:

    LucMeekes_0-1648645063269.png

    or, directly:

    LucMeekes_1-1648645132121.png

    According to the manual, Mathcad 11 uses the Modified Ridder's method (Press et al., 1992; Lorczak). Then appendix L reveals that Press et al. refers to 'Numerical recipies', and Lorczak refers to 'The Mathcad Treasury'.

    They must have broken something between Mathcad 11 and 15...

    Ah, and your sheet:

    LucMeekes_3-1648646072069.png

    And of course you have this variant. Note the red star!

    LucMeekes_4-1648646222106.png

     

    Luc

    V
    24-Ruby IV
    ValeryOchkov24-Ruby IV
    24-Ruby IV
    April 4, 2022

    When I was little, adults told me that taking a derivative numerically is an operation that is incorrect from the point of view of mathematics. For this, children are punished - they are put in a corner.

    палец.png

     

    Terms & ConditionsCookie settingsAccessibility statement