Derivative of Kelvin Function

[dchandiramani]

Prime has built in kelvin functions ber and bei.

I would like to know if it also has ber' and bei' which are derivatives of the Kelvin function.

Thanks.

[LucMeekes]

They are not predefined. If they existed, I should think they would be called Dber and Dbei, similar to the derivatives of the Airy functions DAi and DBi.

But that should not impede you to use them:

Or, in Prime:

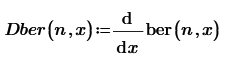
Success!

Luc

[LucMeekes]

Prime knows even how to express them symbolically:

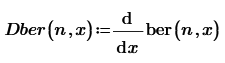
gives:

because:

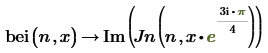
Luc

[Werner_E]

LucMeekes wrote:

Prime knows even how to express them symbolically:

Opps! Is that new in Prime 4 ?

Here in Prime 3:

EDIT: Not my day!

Had overlooked your first post and had not noticed that you also defined the derivative yourself in the second one.

[LucMeekes]

I guess it is. 15 days left to play... (and be terribly annoyed by the slow UI).

Mathcad 11 symbolically gives:

Not more than what you have there in Prime 3.

Luc

[Werner_E]

Guess you misunderstood my post.

At first glance over your post I had the impression, your version of prime would know about Dber and Dbei out of the box. It was only after pressing "Add reply" that I noticed you defined them manually, too.

In Mathcad 15 the symbolics does not know anything about bei and ber, but also in Prime 3 the symbolics knows about "bei" and "ber" and gives us the appropriate result for the derivatives:

[LucMeekes]

Guess you're right. Misunderstanding.

Anyway, I conclude here that something was changed going from Mathcad to Prime, and this change is an improvement.

Luc

[Werner_E]

Agreed on and I am surprised that the change relates to the symbolics as so far I thought thats an area they didn't tamper with.

[Werner_E]

Prime does not provide those derivatives of those Bessel functions out of the box, but you can define them yourself:

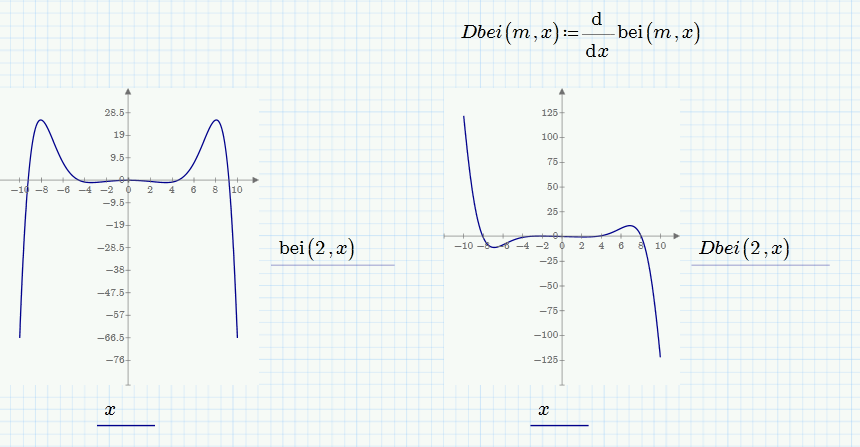
You may even use the prime symbol ' in the name by first writing the name as text between quotes "...." and then deleting the quotation marks.