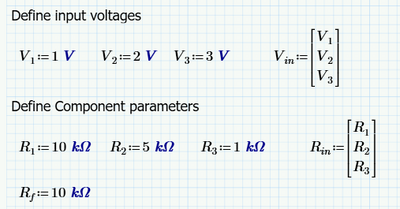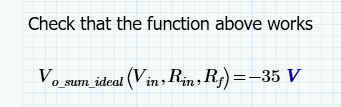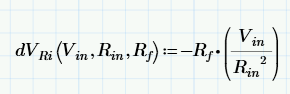Community Tip - Have a PTC product question you need answered fast? Chances are someone has asked it before. Learn about the community search. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Derivative of a function with vector arguments
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Derivative of a function with vector arguments
I'm using Mathcad Prime 5.0.
I have the following function defined.
The intent if for this function to be very generic and allow any number of inputs. Therefore, Vin and Rin are vectors of the same length. Here's how those are setup.
The function itself works fine.
Now, I need to take the derivative of that function with respect to the individual components of Rin. The intent is to estimate how much effect the variation of each individual component has on the overall output. Ultimately the expression and number of parameters will be bigger than what I've shown here. I just scaled everything back to a simpler example to illustrate the actual problem. I was hoping the derivative with respect to Rin would give me a vector of the numerically evaluated derivative with respect to each individual resistance. Instead it tells me everything has to be scalar.
I found some old posts similar to this dating back to 2004 and 2005. They basically said this isn't possible. I was hoping something may have changed in 14 to 15 years.
Thanks,
Jon
- Labels:
-
Calculus_Derivatives
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
was hoping something may have changed in 14 to 15 years.
Unfortunately not (apart from the development of Prime which actually is a big step backwards).
You will have to find a workaround which sure is not as generic as you'd like it to be 😞
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fred,
Thanks! Your approach didn't quite give me what I wanted but it got me thinking.
What I was trying to get was an approximate, linearized effect of each component on the output. Your solution gave me the sum of the derivatives for each component.
But, your approach got me thinking that I was being too lazy in trying to let Mathcad do all of the work. The partial derivative with respect to each resistor in my input vector just boils down to this:
Then, I can just pass my input vector to that function and get my individual results:
Thanks,
Jon
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mathcad is a great tool, but not the best one you have. NASA went to the moon with pencils and slide rules!
Glad you got to your solution.
BTW, Version 15 will allow you to let partial derivatives show as partials (greek d). It also has a gradient function (cntrl-shift-G) that would allow partial derivatives of a function of several variables.