Community Tip - Did you know you can set a signature that will be added to all your posts? Set it here! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
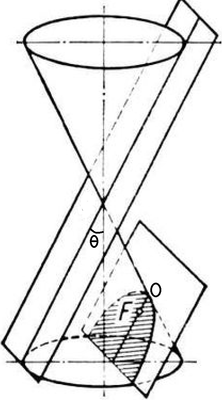
Cone, plane, parabola
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Cone, plane, parabola
With cone? plane and ellipse all is cleare.
See please cone, plane, parabola
Thanks!
And what about a parabola?
I know O-F - can I calculate the theta?
Can the cone axis goes through the focus of the parabola?
- Labels:
-
Algebra_Geometry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Same answers (no to both questions) as in the other thread, same way to see/prove it - Dandelin sqpere - there is only one in case of a parobola and it still touches the plane at the focal point of the parabola which can't be on the axis (as we would have a circle as intersection in that case and not a parabola.
With given plane, O and F you can put a Dandelin-sphere of any radius touching the plane in F. Depending on the radius of the sphere you get cones with different angles.
Your angle theta can be simply calculated by theta=arctan(OF/r) when r is the radius of the Dandelin-sphere which you can freely chose.
- Tags:
- o to both questi