Community Tip - Did you know you can set a signature that will be added to all your posts? Set it here! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Derivative of function
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Derivative of function
Hello,
Yesterday Werner helped with the derivative of the M(x) function, and it was working. Today it is not. I am not sure why. Please scroll down until you see the red arrow. Thanks!
Solved! Go to Solution.
- Labels:
-
Calculus_Derivatives
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It has got something to do with your Moment function.
Define the derivative next to the graph in your sheet and you can see the derivative does not return a zero, therefore the root fails.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It has got something to do with your Moment function.
Define the derivative next to the graph in your sheet and you can see the derivative does not return a zero, therefore the root fails.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mike Armstrong wrote:
... the derivative does not return a zero ...
This is because, although the function is continuous at "a" the derivative is not. The function has a kink, which means the derivative has a step. You need a smoother transition between regions.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Cheers for the explanation Alan. I knew there was an issue but lacked the vocabulary to describe it. ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Alan,
Thank you for the explanation. How do i make the transition smoother between regions? Thanks!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Depends on what the physical scenario is? What happens in reality there? Could try fitting a quadratic curve to points either side of "a". Or cubic spline?
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
sameer fares wrote:
Alan,
How do i make the transition smoother between regions? Thanks!
Here's a simplistic approach!
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Well done.
I guess an error of 0.9% will be tolerable.
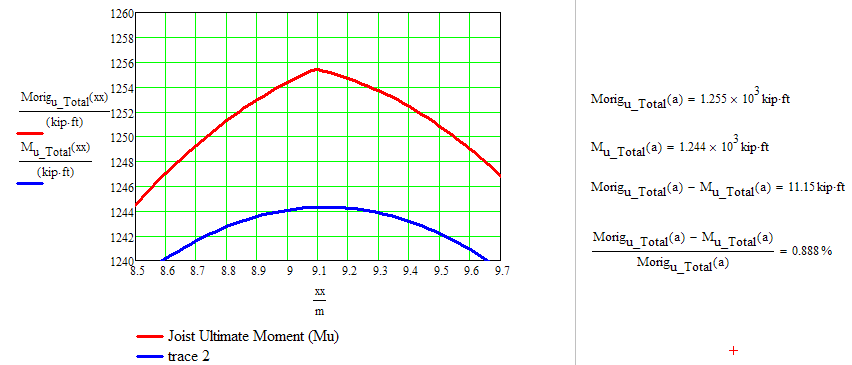
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The shear in your structure is the derivative of your moment curve. IFindthe point of zero shear and you find the point of max (or min) moment.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The error message "These values cannot be compared" is misleading unfortunately. The real reason, as Mike and Alan already pointed out, is, that getting the extrema by setting the first derivative to zero will only work for well behaved continuous functions. You had luck yesterday and bad luck with the new function today, as the derivative seems to never get zero and even if it would it probably wouldn't be the absolute maximum.
Yesterday I wrote "I guess your solve block may be more versatile and probably more robust when we come across more "ill-natured" functions". Thats proves true today, even though I should have written maximize instead of solve block (you can delete the "Given" - you can use maximize as a standalone function.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Very informative response Werner as usual.
As you said the error message is useless, however, the trace error feature did lead me back to the condition were a was included which I was impressed with.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mike Armstrong wrote:
Very informative response Werner as usual.
... and wrong, too 😞 The way the two parts are joint, namely without a step, if the derivative would get zero, it would yield the absolute maximum. I was playing around with the function and suddenly look at an Mu_total with a decent step in it - that way I was misead to the remark.
BTW, here is a closeup of the position where the two parts join and we clearly see the kink Alan was talking about. So it obviously won't help looking for a horizontal tangent.
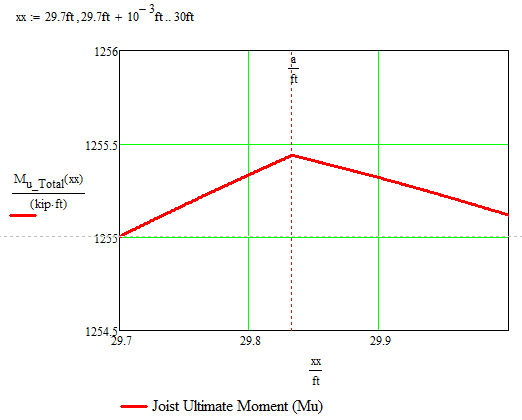
I still meditate over the error message and wondering why we don't simply get the standard "This calculation does not converge to a solution" error. Obviously the error is thrown by the derivative calling the function, but what would root feed into the function as argument that it would not be allowed to be compared to length a. I already tried a unitless variant but with the same error message.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK, the secret about the misleading error message is disclosed. I threw in a trace command (in Mu_total()) and looked what values come in. root is really trying hard to find a solution, playing around x=9 (values are to interpreted as meters) eventually at the end goes havoc. Suddenly guess value number 6824 is 32.004 (out of the blue) and at the end guess no. 6848 is a complex number (32.004 + j*1.024...) and that is why the comparison is (correctly) throwing that error - we cannot compare a complex number to anoter for size, there is no linear order in the set of the complex numbers.
In case anybody is interested I attach the sheet (everything not necessary for the function to work was deleted) and the trace output. Of course I had to modify the function Mu_total a bit to make it work - replacing the last if by an otherwise statement.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Good work and extremely informative.
Still a little confused why the root function doesn't work though.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Still a little confused why the root function doesn't work though.
Because there simply is no solution. There is no point where the first derivative of this piecewise function would be zero. root does its best to search for it, but if its near x=a and changes x ever so slightly, immedeatly the function value (derivative) will jump from positive to neagtive and vice versa. I don't know much about the algorithm used and how its implemented, so I can't tell why root tries with that much larger values at the end and finally arrives at a complex number for x to try with /which then triggers the error.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Because there simply is no solution. There is no point where the first derivative of this piecewise function would be zero. root does its best to search for it, but if its near x=a and changes x ever so slightly, immedeatly the function value (derivative) will jump from positive to neagtive and vice versa. I don't know much about the algorithm used and how its implemented, so I can't tell why root tries with that much larger values at the end and finally arrives at a complex number for x to try with /which then triggers the error.
Sorry, I understood why it doesn't work I was more refering to algorithm used by the solver. Cheers for the explanation.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Good point Werner,
It's strange because I managed to get the root function to return the correct answer although the graph didn't look right.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It's strange because I managed to get the root function to return the correct answer although the graph didn't look right.
In the sheet you posted? You had changed the function Mutotal to something completly different (BTW, the last otherwise statement would never apply) and the maximum is in your case to the left of a (where the step occurs). So the function is well behaved in the erea of the maximum and so root() can do its job - there really is a horizontal tangent at the point maximum. In the original problem the maximum is exactly at the point of joint and no horizontal tangent, we have a step in the first derivative at that point which makes root fail.





