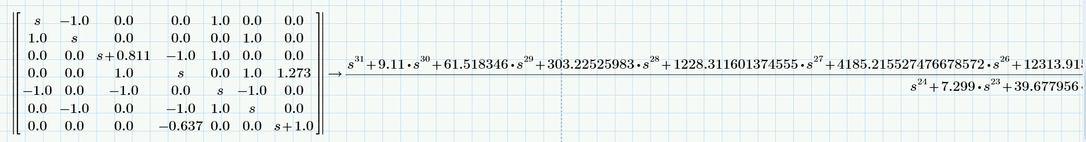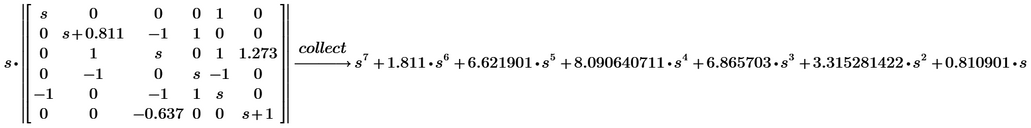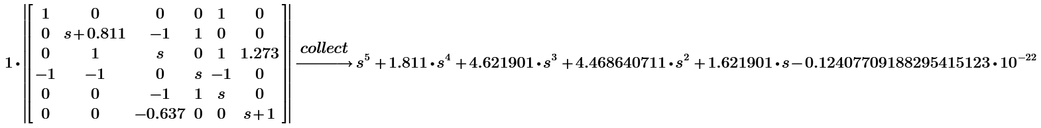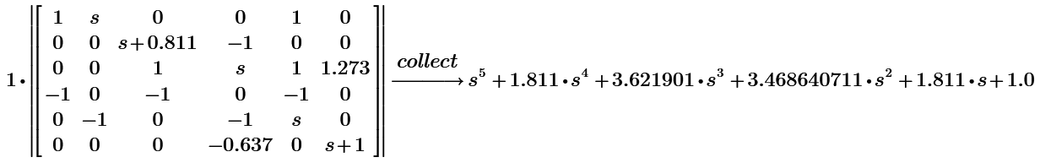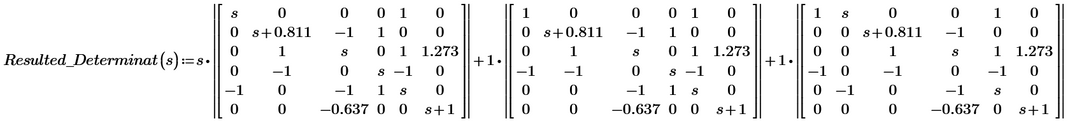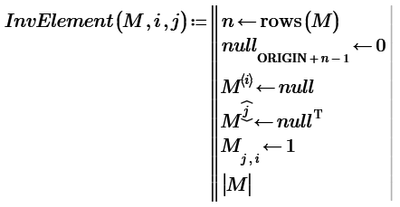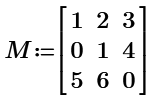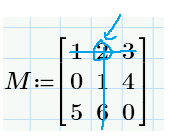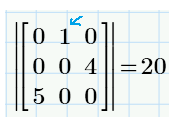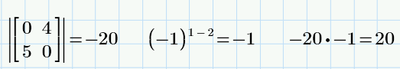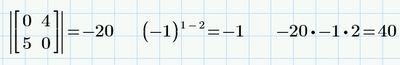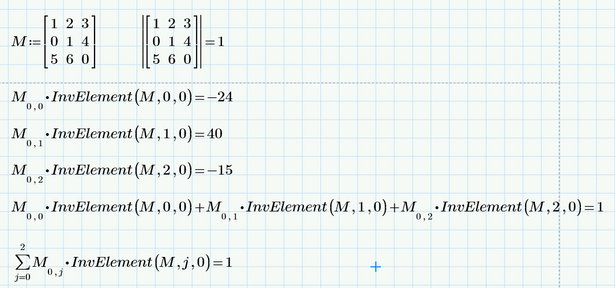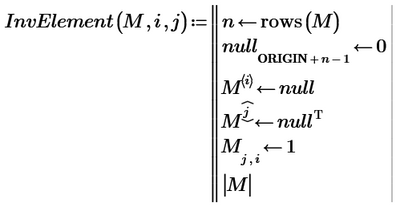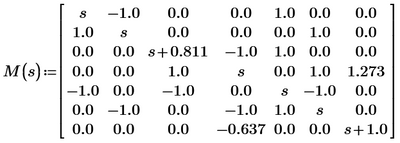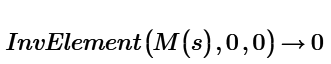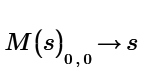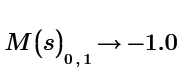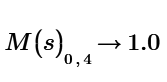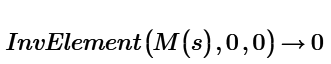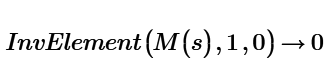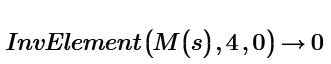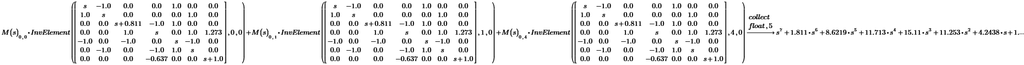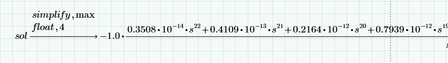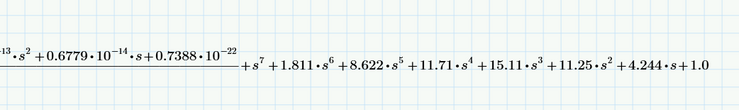We are aware of an issue causing pages to load incorrectly for some users and expect a fix soon. Sorry for the inconvenience.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Determinat of a Matrix Mathcad Prime 8 Strange Result
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Determinat of a Matrix Mathcad Prime 8 Strange Result
Hello,
Mathematica result:
Maple result:
Mathcad 11 result:
Mathcad 15 result:
Mathcad Prime 8 result:
Why does Mathcad Prime give such a result when calculating the determinant of that matrix? Is this some bug from prime? or?
Mathcad Prime 8 file attached.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In Maple you have a typo - first row, second column
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Did not influence pretty much...
Anyway, strange how Mathcad Prime calculates this determinant...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
still quite a large difference compared to the other solution! Look at the coefficients of s and s^2. All other programs get 4.2 and 11.3 but the result of Maple significantly differs!
In P8 you may try modifiers like "collect,s", "expand" or even just "simplify".
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
"In P8 you may try modifiers like "collect,s", "expand" or even just "simplify"."
I already tried and nothing...
And I don't really see what else to do, because we simply have the matrix and apply the determinate (| |) to it...
Is this not a bug or something in Prime, because it calculates like this?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
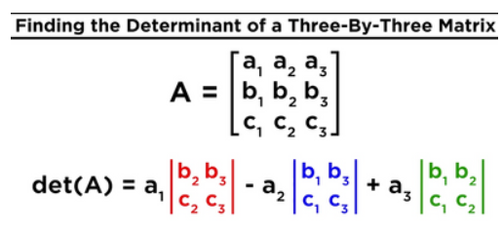
A function like this (to do these kinds of calculations) should be created I think:
https://www.mathsisfun.com/algebra/matrix-determinant.html
But this function should also be valid for calculating the determinant of a matrix larger than 3x3 as in the example above...
@Werner_E @LucMeekes
Does anyone know how to make a function like this?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Werner_E @LucMeekes @ttokoro @Fred_Kohlhepp
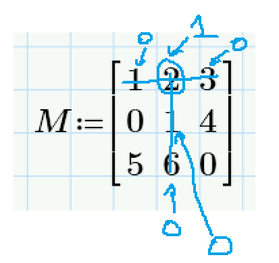
Mathcad Prime 8 result (as shown above):
Calculation with the formula above (hand calculation):
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yeah, you sure could write something like the Lagrange expansion using recursion, but chances are that symbolical evaluation still fails or explains that the result is too large, etc. I would say that writing a working function to symbolically calculate the determinant of a matrix is a job for the development team at PTC.
Did you already report your various problems with the symbolic calculation to PTC support?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
"Did you already report your various problems with the symbolic calculation to PTC support?"
No, I don't know how to do this.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Cornel wrote:
"Did you already report your various problems with the symbolic calculation to PTC support?"
No, I don't know how to do this.
Maybe @VladimirN or @DJNewman can provide information about the current way to do so.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- You need to have a support agreement with PTC (a normal subscription licence includes this; Mathcad via a perpetual licence requires being up-to-date with maintenance payments) to access the case logger: https://www.ptc.com/support/case-logger
- Follow directions; it's a whole series of interactive drop-down menus and text boxes. Don't check the sensitive data checkbox unless it's sensitive intellectual property you wouldn't share on the community
- Be sure to scroll down past the suggestions that you look through existing documentation and community resources and click to open a case with PTC
- You'll need your SCN (Service Contract Number); you can find it in various places, including within Mathcad itself in the window where you configure your licence (the "Service Contact #")
- Be sure to attach the worksheets
I know PTC employees may have a little different workflow than what normal customers have, but the above should suffice.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Until then...I think we can use your function of calculation of minors of a matrix also for calculating the determinant of a matrix.
Here also calculate minors, but instead of putting the common element to be 1 as it is in the above function, the common element must be that number when we want to calculate the determinant of a matrix.
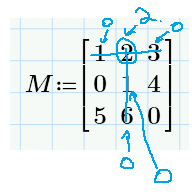
So, for example, if we have a matrix:
And if we want to calculate the minor:
With your function we get:
Classically we get:
But if we want also to do this:
We have to multiply that minor by the common element (and ignore the sign, because the InvElement function already takes its sign into account), so not by 1 as it is in your function.
So, with the above example, we should have:
How can we do this in the above InvElement() function?
And at the end, the sum of each element multiplied by its minor must be made, but now let's see if it is possible to do what I said first/above, and then step 2 is to make the respective sums.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How do I make it so that when I put instead of the matrix, a function to which I assign a matrix, to get the result as in the first case when I put a matrix? (this is for symbolic computation. Numeric computation is ok as seen from the previous post)
Another thing:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is my attempt for a function to calculate the determinant of a square matrix.
First we define utility functions to delete rows and columns of a matrix
Then the determinant is calculated by Lagrange expansion after the first column - done recursive until we arrive at an 1x1 matrix
I haven't tested thoroughly, but it seems to work quite well, BUT ... its VERY SLOW when evaluated symbolically!!
Furthermore something like "simplify" or "expand" is necessary as otherwise the result isn't really nice 😉
Have fun and use at your own risk!
EDIT: Added an alternative function to delete rows (and columns) which avoids the slow "submatrix" function but it did not speed up the calculation.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How can that fraction be made to stop appearing? Is it possible to do that, somehow? Because we see that the numerator tends to 0...each variable s of numerator is multiplied by at least 10^-10, and at the final of the fraction we get the correct answer of the determinat.
Or would the only option be to manually extract the correct result of the determinant?