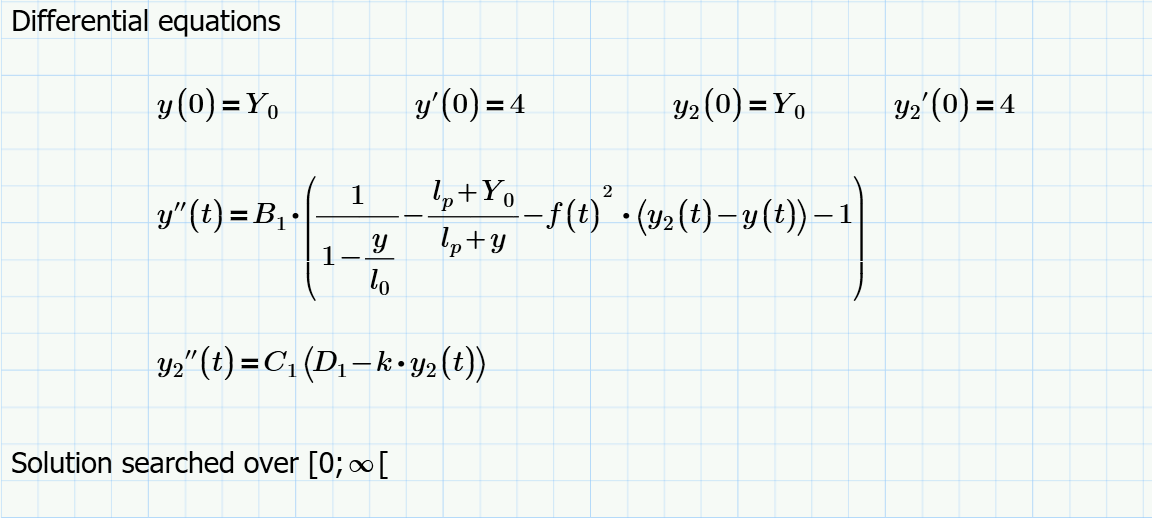- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Differential system
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Differential system
Hi,
I'm trying to solve following system of non linear equations.
Can someone help me to put it in the correct form? I'm not familiar yet with Prime 4.0 and the different solvers.
Thanks a lot.
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have tried y(0)=0 in your/my former sheet (without the units) and I don't get an error if I use the last, optional parameter of odesolve (nsteps=number of steps) and set it to something higher (10^6) than the default 10^3. But the calculation will not stop if I do so. Changing the IC to y(0)=10^-19 works with nsteps=10^6), but the result obviously is not what you expect.
I also noticed before in experiments I made with your older sheets that your ICs concerning the derivatives where not respected by Mathcads solutions. You had y'(0)=y2'0)=4, but the numerically derived derivates of the solutions always differed significantly.
I used the older sheet as your new one is a little bit too confusing for me and because I think you should not add units until the unitless version works OK - especially as you make the solve block unitless not by dividing by the base units but use mm and ms, which I think is additionally failure prone.
I clearly have no idea whats the problem with your system and so I am just poking around.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mathcad will solve this best numerically; for that you would need to define a value for all constants.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for the answer. All the constants and functions are defined in the attachment.
I can solve this numerically like on excel yes but I was hoping there would be some function or better way to solve this than to do y(t+dt)=y(t)+y'(t)*dt
Thanks anyway.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The following is unclear, missing etc:
- k is undefined
- y is undefined (or did you mean it to be y(t)?)
Look up the help information regarding solving differential equations using a 'solve block'.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As was already said you did not define k and used y (presumably instead of y(t)).
Another error is that you typed C.1(D.1....) instead of C.1*(D.1...). That way this C.1 is seen as an unknown function.
As you can solve only numerically, you have to provide an upper limit for t. The lower limit 0 is derived automatically from the initial conditions.
Normally you would use a solve block with odesolve to do the job, but for some reason unknown to me this solve block fails (as so often in Prime with an unknown error).
You can solve for y2 first (it does not depend on y) which works OK and use the result in a second solve block for y. Unfortunately this second solve block fails again. So for some reason Prime seems not to like the equation for y''.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry for the small errors on my side. The first equation is easy to solve without using mathcad (especially the odesolve bloc doesn't work for me for some reason). I added this equation in the system because I want to add a non linear component to it in a further stage...
My problem is clearly with the second, not linear one which can't be solved by odsolve (according to the help files it can only solve linear ODE).
I've thus tried several options to solve it numerically but I'm sure my way is not optimised and it really takes forever to solve it... (see attachment)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In Prime you have to create a special region, a so called "solve block" where you put your IC and equations
Mathcads abilities with DE is not really top notch and can be quite tricky.
It may be the non-linearity which is the cause for the solve block failing, but I can't be sure about that. After all the help states that it must only be linear in its highest derivation which your equation is.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
"After all the help states that it must only be linear in its highest derivation which your equation is."
I have my doubts... The first term on the right side has a y {I think we concluded that it is y(t)...} in the denominator. To get it away from there, you'd have to multiply all terms (left and right) with (lo-y(t)), that gives at least a y.y'' term.
Luc.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
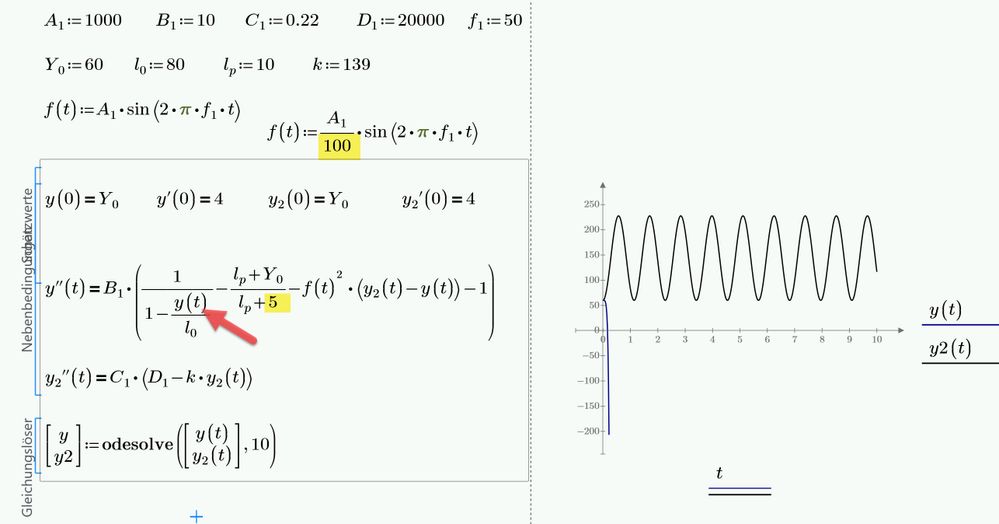
You are right. but if I change one of the two y(t) in the denomitors to a constant value (5) and if I use a smaller amplitude for f(t), Prime surprises us with a solution!?? Even though there still is a y(t) in the denominator!
It may be the resulting y"*y^2 which is the cause for the original equation failing, but then - if I exchange the y(t) in the first denominator for a constant and let the second, the block still fails.
So I am really not sure what exactly makes the solve block fail and if it would be possible to find a workaround.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
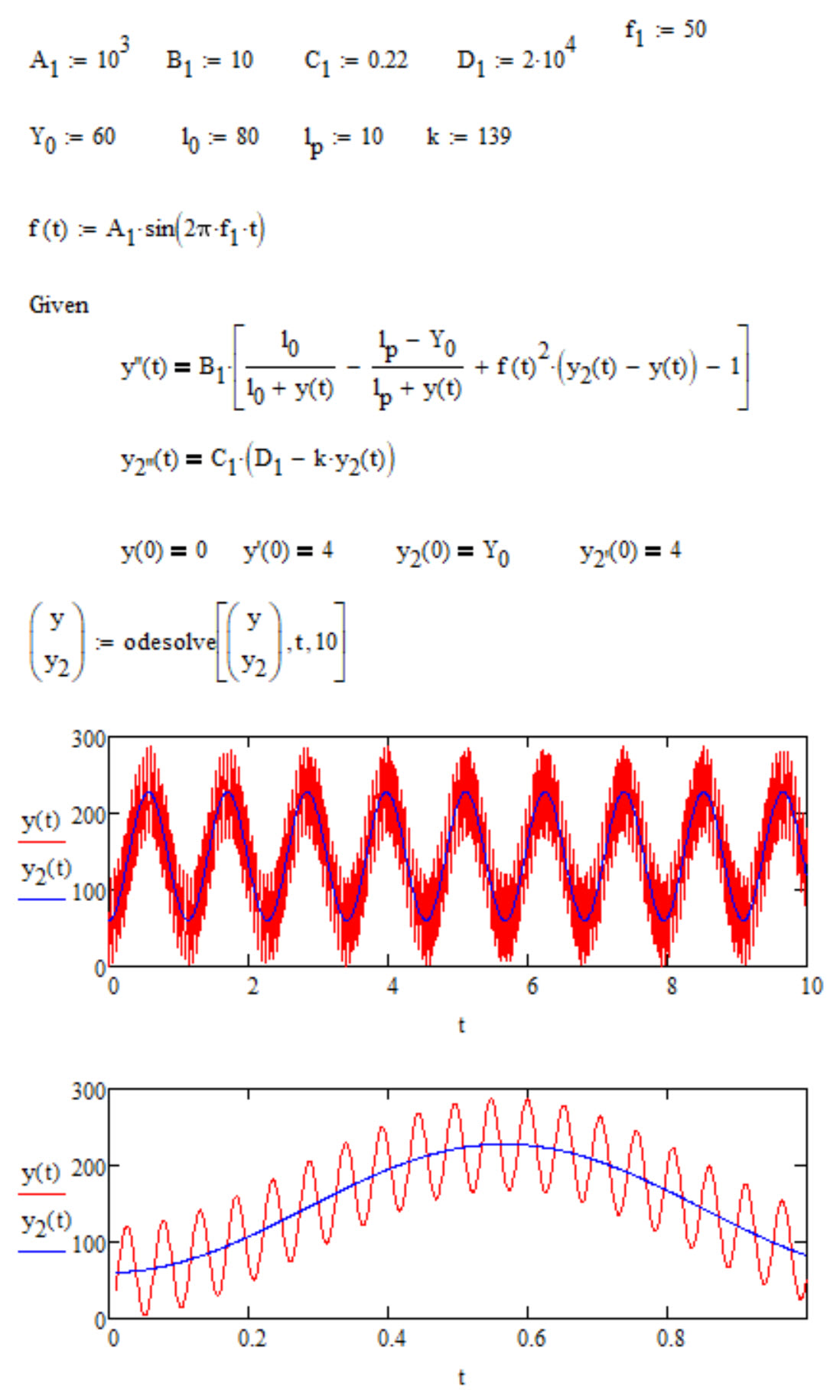
Just gave it a try with real Mathcad and the system solved as it should. Hope I didn't make a mistake by retyping the equations.
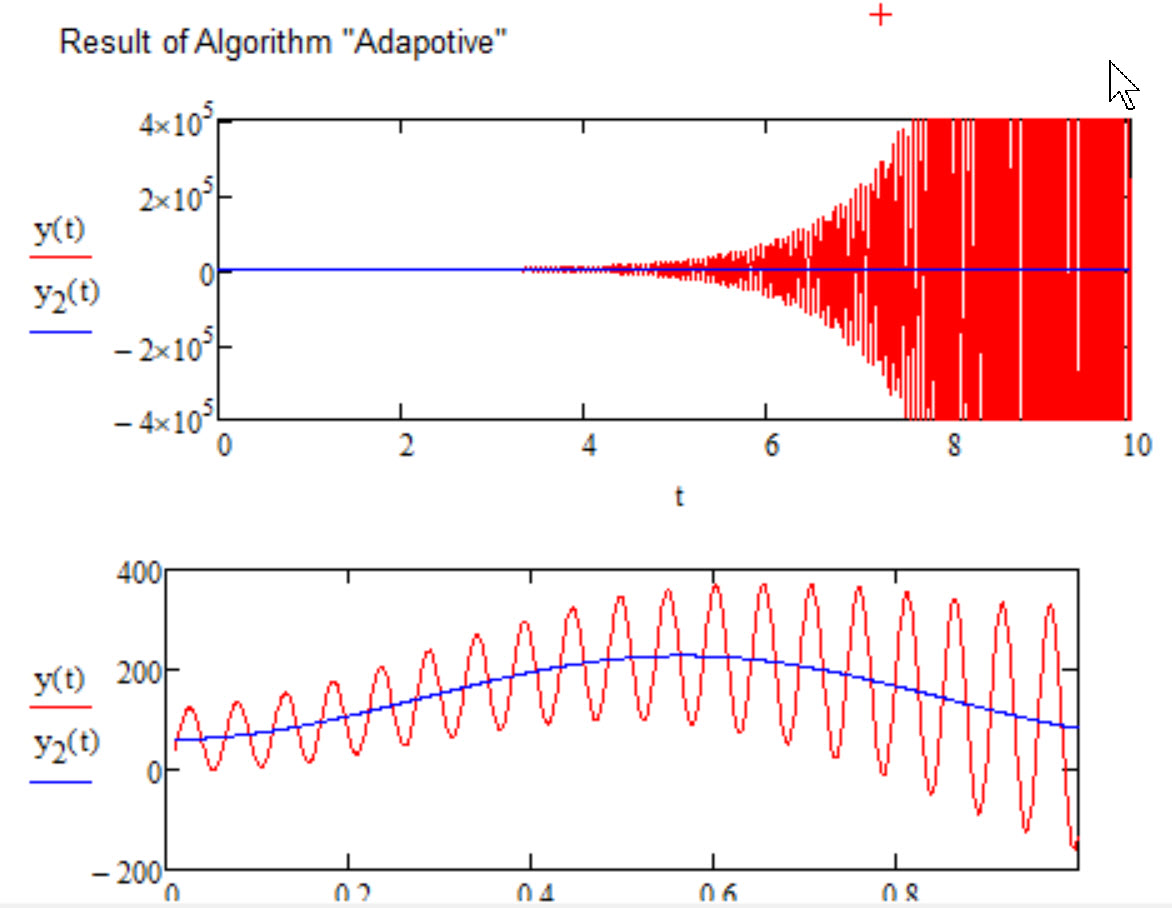
Algorithm used in the screenshot below was "Adams/BDF". "Radau" gave the same result, "Fixed" failed and "Adaptive" seems to produce a wrong result (second screen shot).
Guess the problem in Prime is once again a problem with the new highly praised Knitro algorithms. In Prime we have no algorithm choice. Maybe someone wants to report it as a bug.
With "Adaptive":
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This ODE (in the OP sheet for y2) is trivial and is not the problem.
The problem is the second ODE for y - the one that also references y2.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
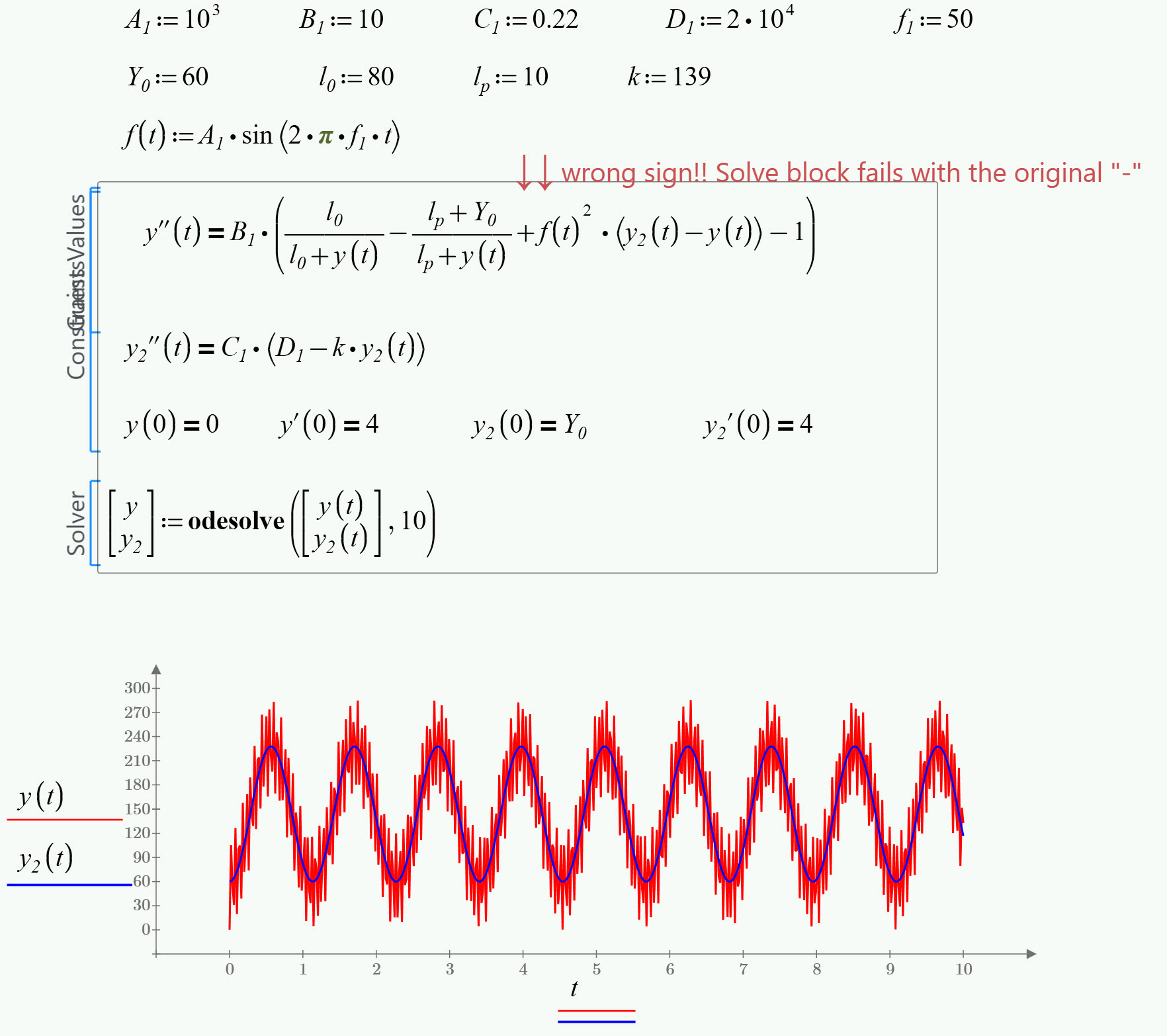
OK, I was wrong about Knitro!
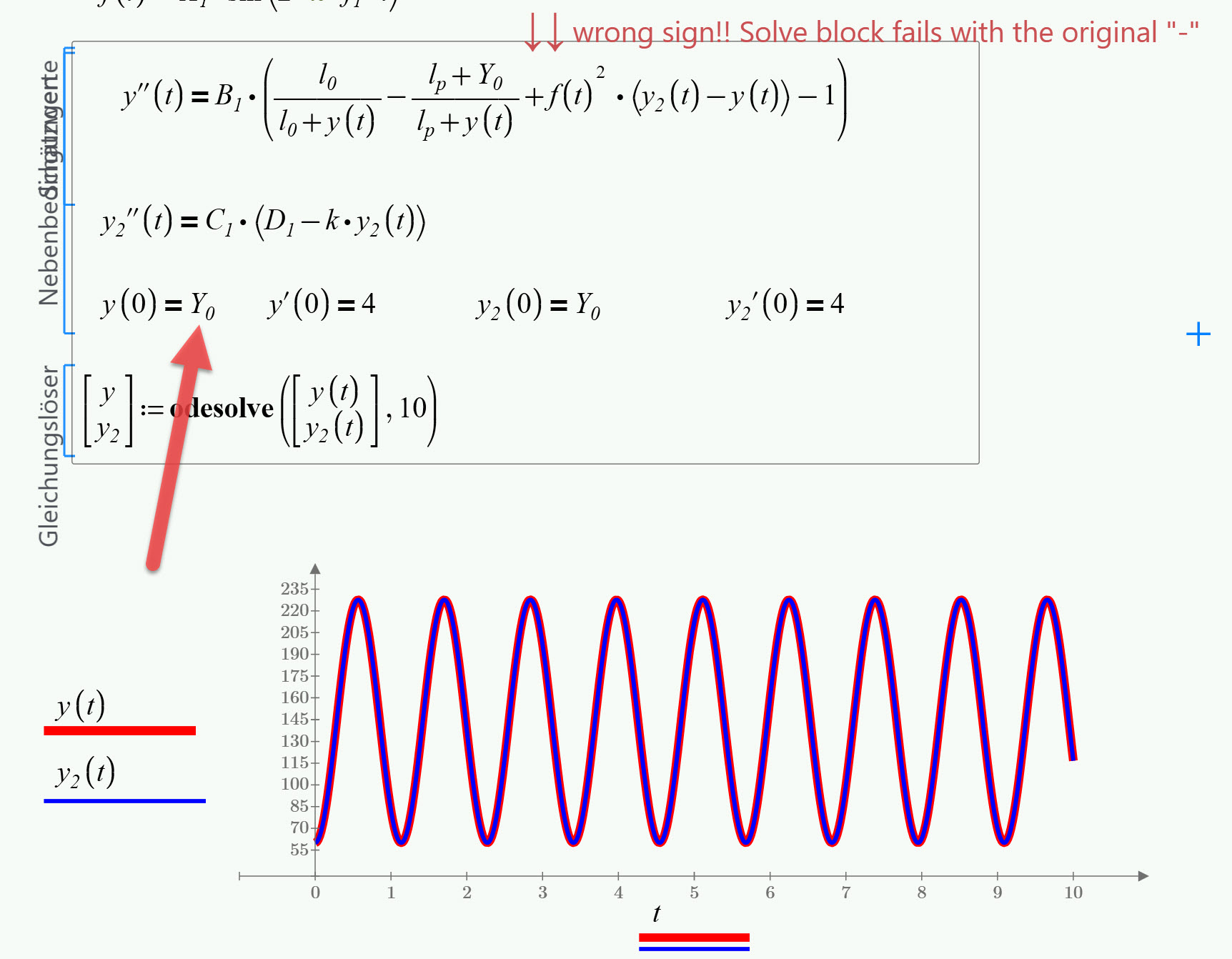
I had two wrong signs in my Mathcad 15 sheet and one of them made the whole solve block work.
Using the original sign makes the block fail in Mathcad 15, too. Error message is "Divide by zero".
Using the wrong sign in Prime makes the solve block work as in MC15.
Fazit: The problem is not a bug in Knitro and its not because of some non-linearity of the equations.
Are you sure, the equations are correct and have a solution?
Here is the result of Prime using the wrong sign. Worksheet in P4 format attached.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Need more coffee!!
Just noticed another mistake I made when I retyped the system in MC15. One of the IC was wrong.
With the original ICs (the same for y and y2) the result seems to be y=y2.
But still a result is only obtained using the wrong sign as indicated.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Using the knowledge that y2 can be solved independently from y, and using Mathcad 11, I get:
Does this come close to what you expect?
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
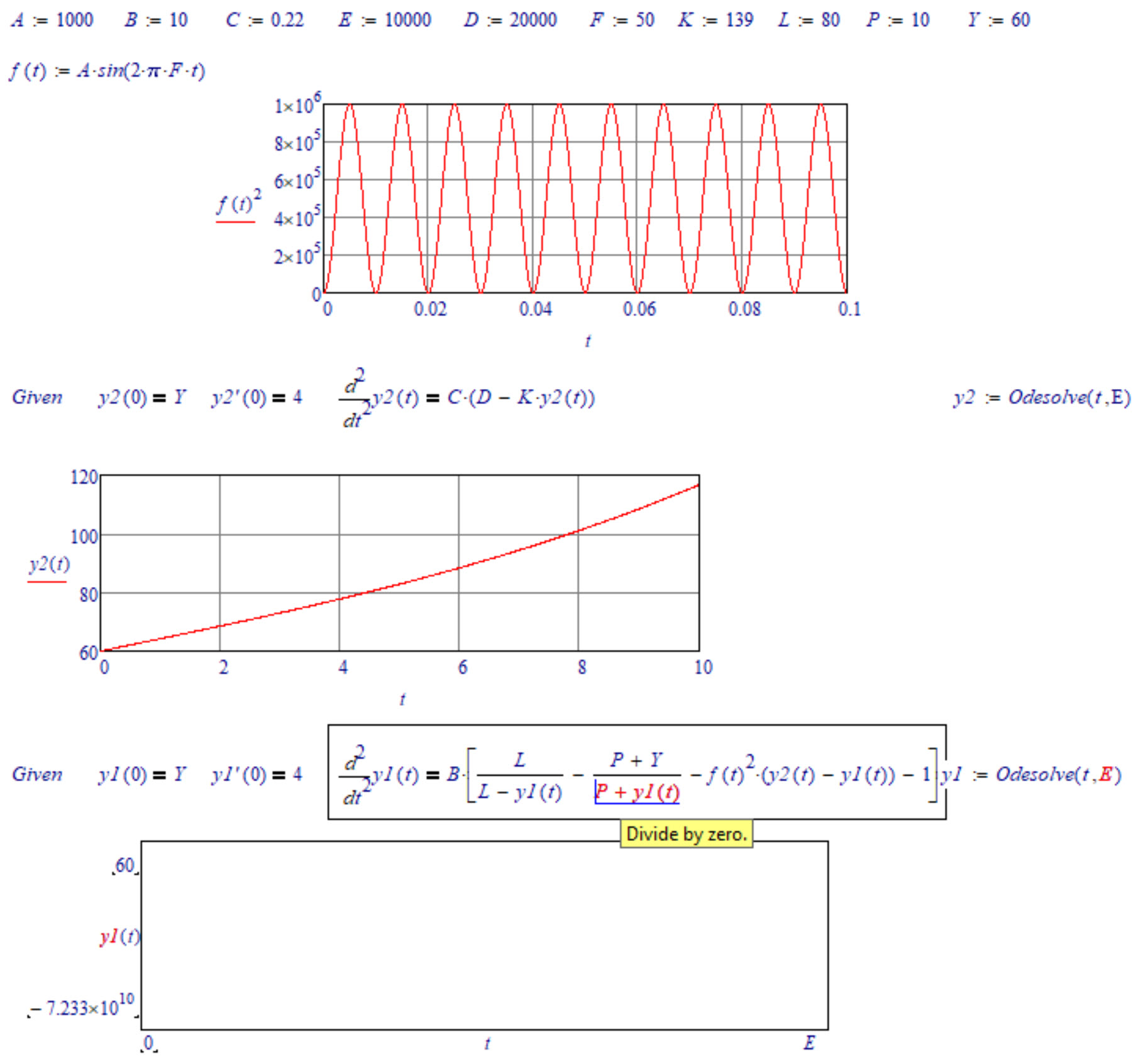
Below is what I get when I open your sheet in MC15.
Interesting is the wrong result for y2. This is due to the high endvalue 10^4 for t you had chosen. Only get the correct solution if I add a higher value for the number of steps -> y2:=odesolve(t,E,10^5)
As you can see the second solve block fails again with a "Divide by zero" error.
What did they change in the numerics on the way from MC11 to MC15 ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Werner,
I went again through the equations and put that in your file using mathcad 15 (way more familiar with that one than the prime version). I checked the different values and corrected some I overevaluated.
I think also the problem is of convergence so limit conditions.
I put these conditions in the equations of both y and y2 but well, Mathcad doesn't like it and I couldn't solve this problem separately either...
Thanks for the answers also.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I sure share your feeling about Mathcad 15 🙂
You forgot to define F.0 which is used in your second equation.
After assigning an arbitrary value I get a result (just used global variables to make it easier playing around with different values.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
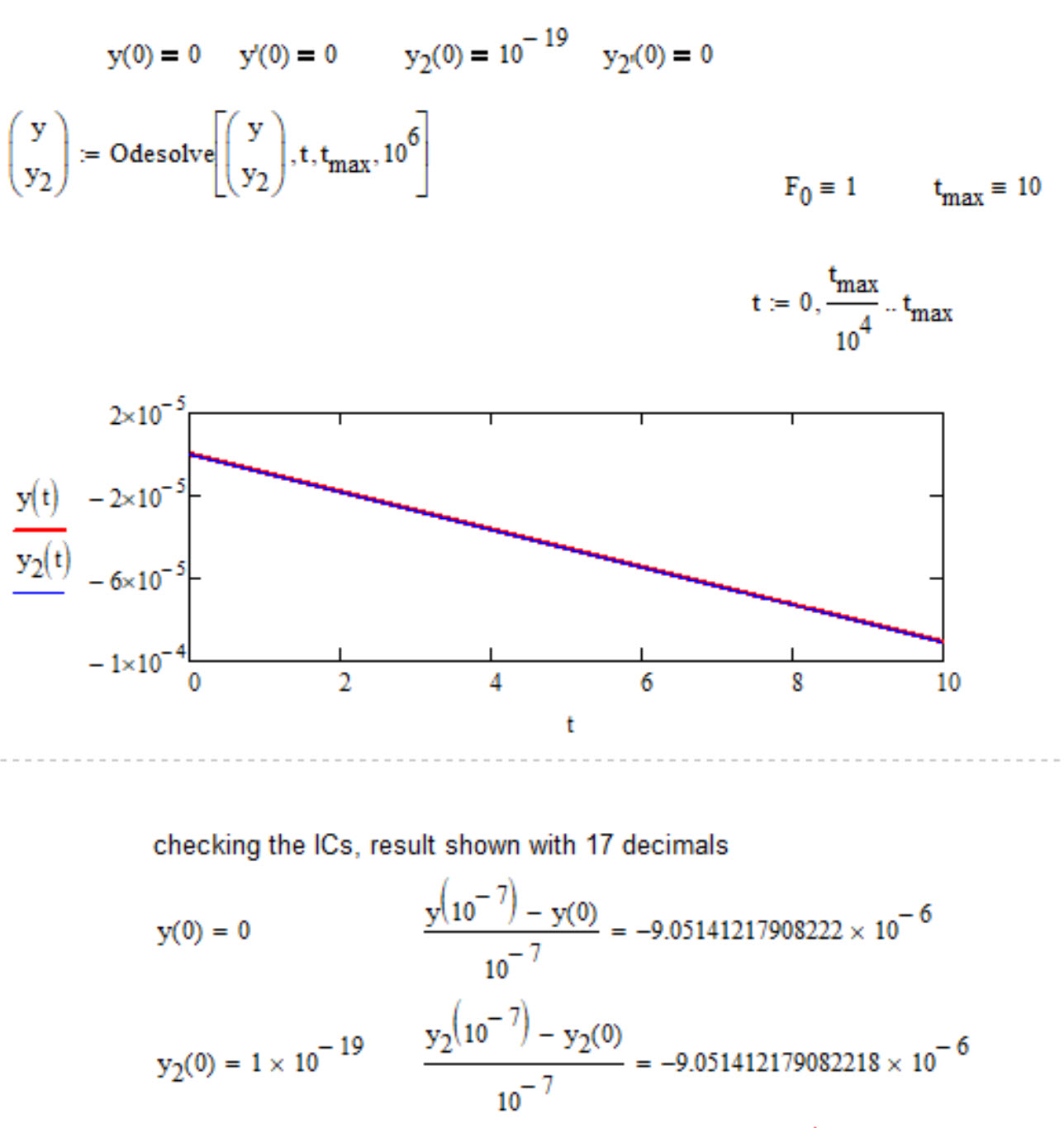
I made another mistake with initial conditions: y2(0)=0.
Problem is the system is not solved with these initial conditions. I need to give non 0 values which don't fit to my problem. Also when i slightly change tmax the solution change completely: with tmax=0.01s I reach 60 within 8*10--3 but with tmax=0.02s i get 0.5 within the same time...
I actually don't trust the results I got there.
The results I got with tmax=0.01s are closer to what I'd expect in reality. but then the rest is clearly not. Is there some other issue I didn't get? Is the Odesolve really appropriated?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have tried y(0)=0 in your/my former sheet (without the units) and I don't get an error if I use the last, optional parameter of odesolve (nsteps=number of steps) and set it to something higher (10^6) than the default 10^3. But the calculation will not stop if I do so. Changing the IC to y(0)=10^-19 works with nsteps=10^6), but the result obviously is not what you expect.
I also noticed before in experiments I made with your older sheets that your ICs concerning the derivatives where not respected by Mathcads solutions. You had y'(0)=y2'0)=4, but the numerically derived derivates of the solutions always differed significantly.
I used the older sheet as your new one is a little bit too confusing for me and because I think you should not add units until the unitless version works OK - especially as you make the solve block unitless not by dividing by the base units but use mm and ms, which I think is additionally failure prone.
I clearly have no idea whats the problem with your system and so I am just poking around.