Dimensional analysis of fast Fourier Transform

[ClaudioPedrazzi]

Hi everybody,

I do not understand the following: I have a signal, an acceleration: the units are of course [m/sec2].

Now the Fourier Transform of a function should have the dimensions of [function]*time.

So the FFT of my signal should have the dimensions of [m/sec]

What I get (I am actually using cfft, but that should not do any difference)

cfft(acceleration) --> units [m/sec2]

why does this happen? it should be [m/s]

I discovered the problem while trying to compute the Power Spectral Density of the acceleration signal (that is what I actually want). It comes out with the wrong units. I also tried to use pspectrum (from Signal Processing), but I also get wrong units.

Attached a small example where I show my problem using a sample sinusoidal signal + noise

Thanks a lot for any advice!

[Werner_E]

The cfft is using the ordinate values only and doesn't know anything about a time-axis. The values are calculated using

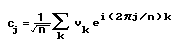
So c must have the same unit as the transformed vector v.

[ClaudioPedrazzi]

Hi Werner!

I see what zou mean, you are right, I did not think about that. May I then ask you (and the other forum readers) what should I do in order to approximate the mathematical definition of Fourier transform,

given a function of time fun(t) approximated through two vectors fun(i) and time(i), with time(i)=i*delta?

Possibly just multiply the result cfft vector by the total sampling time?

I am not so familiar with signal processing: my background is more in mechanics. But I do need to compute the Power Spectral Density of an acceleration signal, and I know that it should come out [m2/sec3]

Thanks a lot for any hints,

Best regards

Claudio

[Werner_E · Accepted solution]

You are just facing the difference between the continous and the discrete FT. In the latter the codomain and so the unit does not change.

Possibly just multiply the result cfft vector by the total sampling time?

Rather with the reciproke of the sampling frequency, that is by the total sampling time divided by the numer of samples.

What you get using an FFT is essentially the complex amplitudes (scaled, differently for CFFT or cfft). The abscissa is a dimensionless scale - just indices. To get the corresponding frequency f of a given index i you would have to use f = i * Fs / N, where Fs is the sampling frequency and N the number of sampled Points.

Don't know but may these links can be of help with figureing out the relationship between the continuous and discrete spectra.

http://dsp-book.narod.ru/DSPMW/01.PDF

http://www.gmrt.ncra.tifr.res.in/gmrt_hpage/Users/doc/WEBLF/LFRA/node68.html

[ClaudioPedrazzi]

Hallo Werner!

Thanks a lot for the explanation and the useful links. As I wrote, I'm not familiar with signal processing.

I was not aware of this difference between discrete and continuous Fourier Transform. With a little modification of your suggestion (namely multiplying the cfft result by the total sampling time divided by the square root of the number of samples) I have a very good correspondence between an example whose theoretical Fourier transform is known and the numerical computation. I used a rectangular function.

I hope you can agree with this small correction, after all the square root of N is in the definition of cfft-function by MathCAD. I tested a little with different inputs, and the formula seems to work always.

I am grateful also to all other contributors and as thanks I will post here my actual example. Maybe it could be of use to someone else in the future looking for the same answer. By the way @Fred: I also tested pspectrum but the problem with the units remained. In the attached example the function is used at the bottom, and also needed a little "tampering" to bring the numerical result to the "right" value.

Best regards & thank you everyone

Claudio

[Fred_Kohlhepp]

An FFT (or cfft) doesn't change the units. A fourier transform takes a time history (m/sec^2 vs time) and returns a frequency distribution (m/sec^2 vs frequency.) Why do you believe it should multiply by time?

[ClaudioPedrazzi]

Hi Fred,

the reason I believe this is that I am trying to obtain a PSD of an acceleration signal and I have to compare it with a given PSD, supplied in m2/sec3 (*). Since the units come out different, I was looking for an explanation.

Beside this, dimensionally speaking, isn't the Fourier Transform of the function f(t) an integral of the function in dt, that is shouldn't it have the dimensions [f(t)]* time ?

(*) see page 24 of this PDF

Thanks a lot for your answer!

[Fred_Kohlhepp]

There is a function, "pspectrum," that develops the power spectrum of a signal. Give that a try.

[RichardJ]

Power spectral density is power per unit frequency (in this case Hz). Power is the square of the amplitude. So square m/sec^2, and divide by Hz (i.e. multiply by sec).

[Fred_Kohlhepp]

pspectrum reports units squared (m^2/sec^4 for acceleration.) No division by Hz!

[RichardJ]

The power spectrum will have units of m^2/sec^4. Power spectral density is power per unit frequency.

[ClaudioPedrazzi]

... well, again, I am making my first steps in this field, but at least the Nuclear Regulatory Commission of the USA seems to believe that a PSD of an earthquake acceleration signal has to be in m2/sec3. See page 22 (and following) of this document.

I don't really understand why pspectrum output this units, possibly the difference is in the continuous vs. discrete transform. Anyway if you look at the file I posted (the last one, with the rectangular test function), I had to multiply the output of pspectrum by deltat and divide it by pi, in order to obtain the "expected" numerical result.

[RichardJ]

The output of pspectrum is power as a function of frequency, not power spectral density as a function of frequency.

[ClaudioPedrazzi]

oh! I see. I thought "pspectrum" = PSD!!!

Well, then, it is simply not what I am looking for, and I will stick to the old good cfft squared, that anyway seems to work good enough.

Thanks again Richard for pointing this out.

Claudio

[RichardJ]

The squared output of the FFT is also power as a function of frequency.

[ClaudioPedrazzi]

Oh well... now I am a little unsure. Thanks for your patience... (I don't want either to abuse of your time).

I programmed the following equation (from NUREG-0800; 3.7.1, Appendix A), linked in previous posts.

I did this (and it seems to provide meaningful numerical results) with the following MathCAD instructions:

Where DeltaT is the Total Time Duration and acc is a sampled acceleration time history of Npt points. The reason I multiplied the result of cfft by the factors you see, is that I wanted it to correspond to the theoretical results for an analytical example (rectangular function), as previously posted. And it does, now. The second step is just the "definition" of "one sided PSD" that I get from the NUREG-norm. And it has to come out in [m2/sec3].

So what do you think?

Basically it all goes back to the question: given a vector of sampled accelerations, how to compute the one-sided PSD as defined above? It has to be dimensionally correct because it has to be compared with a "required minimum PSD".

Probably tomorrow everything will be clearer 🙂

Have a nice day/evening

Claudio