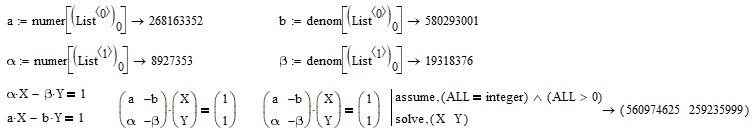Diophantine Linear Equation ?

Forum|Forum|4 years ago
April 10, 2021
2 replies
2327 views

Hello Everyone.

--//--

Thanks in advance for your time and help.

Regards.

6_Diophantine-Linear-Equation.zip

Math Homework

-

-MFra-

21-Topaz II

The determinant gives an equation with two unknowns. However, if I add another one relating to the next ratio, I obtain a non-homogeneous linear system of equations in the unknowns X and Y, of which there is a solution. What do you think?

lvl107 answer.jpg

L

lvl107

Author

20-Turquoise

Thanks for your time, MFra. I guess we should consider something about: . Copy and paste your screenshot, it seems look like the following:

Thanks your time again.

Best Regards.

Loi.

1_Diophantine-Linear-Equation-(-1-).zip

-

-MFra-

21-Topaz II

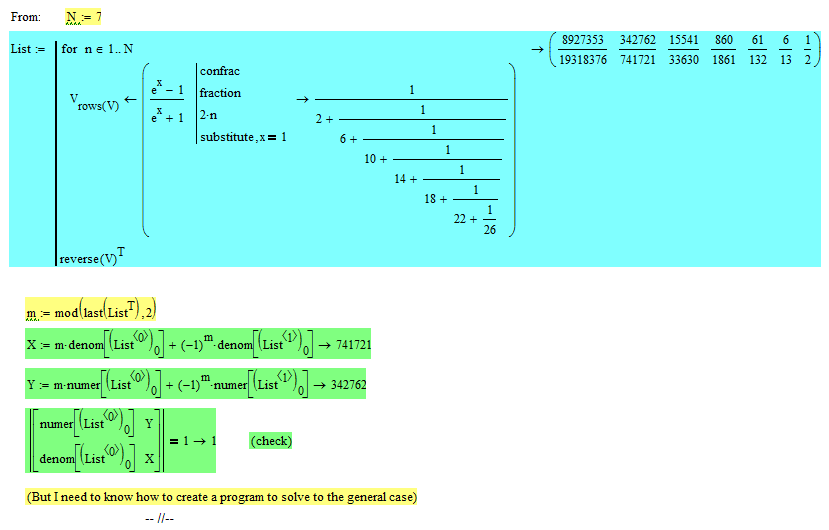
I know it's not the answer you are looking for, furthermore, some are negative and aren't diophantine solutions, but it's already something ....

lvl107 answer 1.jpg

Instead of defining a linear non-homogeneous system of equations with constant coefficients in two variables, in the same way, one should define such a system in N equations in N diophantine unknowns. I don't know if that's possible.

In the group "Gruppo di Matematica" of FB, there is a professor (Domenico Annunziata) who has written a book dedicated to Diophantine equations, you could turn to him for clarification.