Community Tip - Need to share some code when posting a question or reply? Make sure to use the "Insert code sample" menu option. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Displacement Problem
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Displacement Problem
Hello User Community,
So I have another issue similar to yesterday where I am trying to follow the logic to the solution to a problem I have.
Again I am sure this is my poor Algebra skills but looking for clarity.
Below is the problem is the question and the model answer:
The part I am struggling to follow is the displacement mass difference derivation. I follow that:
i.e. the product of the initial density and under water volume must equal the second density and underwater volume. Therefore, the first density and underwater volume is equal to the second density multiplied by the initial volume plus the difference in volumes i.e. the second volume.
I can also follow that:
The difference in displacement mass (between floating in salt water to floating in near fresh water) is equal to the second density multiplied by the difference in volumes which logically is going to give a difference in masses. This being equal to the difference in densities multiplied by the initial volume.
I can also follow that:
by way of dividing rho2 by rho and rho by itself.
What I then struggle to follow is:
The only way I can think of doing this is by substituting volume for displacement mass but surely this would give:
?
Can anyone shed some light on this?
Andy.
Solved! Go to Solution.
- Labels:
-
Algebra_Geometry
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Your algebra is correct. You can show this with Mathcad:

Also, be careful using Delta as a variable. Delta is a built-in function. I had to manually change the label from "function" to "variable".
In your screenshot, the first Delta is non-italicized, but the next three are italicized, so I think they have different labels applied.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The change in displace volume of water due to density change:

The "area" of the ship at the waterline:

The new draught (new volume divided by area:
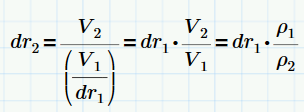

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Fred,
That certainly seems like another way of doing it.
One thing I am intrigued by is that you have suggested waterplane area can be derived by underwater volume/ draft. Would this not give a mean area over the draft i.e. over the entire volume that is under water? i.e. the waterplane area would change dramatically as the vessel floats higher in the water assuming it is not a wall sided ship.
I am hoping that someone can follow the model answer that I have been given and explain how the step I set out above is derived as I am struggling to understand how this has been done.
Cheers,
Andy.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You are correct, my solution assumes a constant area. The difference in draught is 0.07 meters, about three inches. How much do you think the area might change?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fred,
i take your point. trying to understand how this would work mathematically. If you divide a volume by a linear dimension you are left with an area, granted. But what is to say that area would be the waterplane? Surely that area is a hypothetical area of the mean area of the height of the underwater volume. Would a more accurate derivation of the waterplane be to divide the change in volume by the change in draft?
A
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Andy,
Attached is the math of your problem (in Prime 3.0 and XPS.)
Your problem is assuming an area, the attachments show you this.
All real problems have to have units balance.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fred,
Thanks for that. I think you have proven that you get a consistent area out of the maths in either water density by dividing the TPM by the relevant density. This is also achieved through the method I suggested which is to divide the change in volume by the change in trim as this dimension is pretty much the waterplane i.e. where the additional sinkage happens.
However, my original point was that dividing the volume by draft may not give an accurate waterplane rings true as applying this to the worksheet you provided gives 647.874m^2 not the 702.439m^2 that you have calculated. I would however say it gives a good approximation and would give a better idea the closer the block coefficient of the ship is to 1.
Cheers to all,
Andy.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have given this allot of thought regarding the point I am stuck on and am not sure if the algebra is correct so would appreciate a second opinion. Is it correct to act as follows:
Replacing V for Delta/Rho as volume = mass/ density, this can be rearranged to rho-rho2/rho *Delta. This is where I am not sure but I believe that as rho-rho2 is over a common denominator it can be said to be "2 fractions" therefore rho/rho - rho2/rho which is obviously 1 - rho2/rho. Is anyone able to confirm if this is mathematically sound or the ramblings of a sleep deprived student?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Your algebra is correct. You can show this with Mathcad:

Also, be careful using Delta as a variable. Delta is a built-in function. I had to manually change the label from "function" to "variable".
In your screenshot, the first Delta is non-italicized, but the next three are italicized, so I think they have different labels applied.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for that, Had no idea. Everyday is a school day!





