Community Tip - Visit the PTCooler (the community lounge) to get to know your fellow community members and check out some of Dale's Friday Humor posts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Display Calculation Time, How?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Display Calculation Time, How?
Hello,
I am supposed to get cpu execution times for several different matrix manipulations, but I am unsure how to do it. For instance, I need to invert a 10x10 matrix, and then invert a 100x100 matrix, and show the cpu calc times for each. Is there somebody that knows how to do this? i've attached my worksheet.
Thanks!!!
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If we construct a function (calculation time to solve system vs. number of unknown) we see, if we plot in in a log-log scale that it looks approx. like a straight line. Timing in Mathcad isn't that accurate and we don't know how to compensate for time to function call and looping.
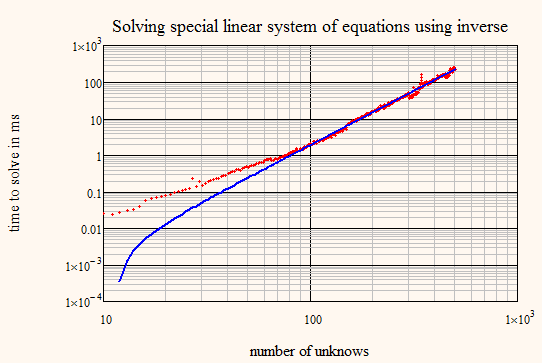
So it seems to be a good idea to try a powerfit
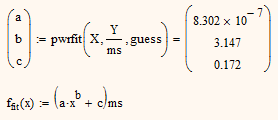
which show that the time is approx proportional to x^3.15 which may be x^3 for more precise timing!?
Also extrapolations using the powerfunction are quite good

Unfortuately Mathcad won't be able to deal with much larger matrices than 4000x4000 but the tendency is well seen anyway.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As long as you ar enot using Prime there is a way to do it.
time(0) (any integer agrument will do) returns a time in second with a precision of ms. Call it before execution of th efunction you wish to time and then after and view the difference. Best done if all is put in a program so you can be sure the time() command will really be evaluated.
For calculations which take not much time to exectute you may use a loop to execute them repeatedly a couple of times.
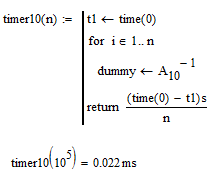
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner…
Prime 3.0 (at least) has the time() function, so I was able to duplicate your program. However, rather than play around with matrix inversions, I substituted other operations for dummy. The fastest operation I found so far was dummy <— 0, which gave me two results: 0.000000000000000 ns and 9.999275207529530 ns. ![]() Of course, this level of precision is absurd, so let's just say 0 ns (7 out of 10 times) and 10 ns (3 out of ten times). dummy <— log(n) produced a variety of results ranging between about 130 ns and 210 ns.
Of course, this level of precision is absurd, so let's just say 0 ns (7 out of 10 times) and 10 ns (3 out of ten times). dummy <— log(n) produced a variety of results ranging between about 130 ns and 210 ns.
BTW, I'm using a 2.5 GHz quad-core Dell Latitude E5520 (Core i5 processor)
All this proves your point below that timing in Mathcad isn't that accurate.
Fred
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Oops! Don't know why I thought time() would not be available in Prime. I should have known better as I now remember vagely an older thread where I implemented some timing routines for someone dealing with rather huge matrices in Prime (probably 2.0 at that time) and it showed that Prime was quite slower in execution than MC15 - at least without multithreading. It was also shown that built-in commands like stack and augment are much(!) slower than self written routines using loops (this applies to both Prime and real Mathcad).
And yes, timing in Mathcad isn't quite accurate but at least it can show a tendency.
I am not sure if we get a better accuracy by placing the loop differently. Anyway, the first try was a bit surprising:

What we see here seems to be that the overhead caused by the loop counter incrementing (in timer1()) is much smaller than the overhead caused by the call to time() and the subsequent assignment to tsum (in timer2()).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
By comparison, in years past I did quite a bit of function and subroutine timing with my HP-41CX calculator to optimize calculator programs and the results were very consistent from trial to trial. That's the beauty of a simple machine with all functions built into ROM. Of course, the functions were MUCH slower and timing precision was limited to 0.01 sec.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here's a user DLL from Robert Adair that is more accurate than the time function. It does not work in Prime, but the cpp project is included, so someone could make a new DLL that would work with not too much effort.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks a lot. Sure soemthing for my toolbox. Those routines at least deliver more consistent results when called multiple times and also the result is not dependent that much on the number of loops. The dll routines seem to have more overhead, though, as the times measured are generally larger than those measured with the built-in time().

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If we construct a function (calculation time to solve system vs. number of unknown) we see, if we plot in in a log-log scale that it looks approx. like a straight line. Timing in Mathcad isn't that accurate and we don't know how to compensate for time to function call and looping.

So it seems to be a good idea to try a powerfit
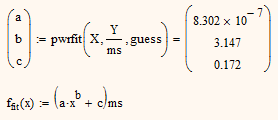
which show that the time is approx proportional to x^3.15 which may be x^3 for more precise timing!?
Also extrapolations using the powerfunction are quite good

Unfortuately Mathcad won't be able to deal with much larger matrices than 4000x4000 but the tendency is well seen anyway.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I ended up having to do my entire homework problem in Matlab. I don't particularly like Matlab, but for a problem like this it was so much easier. I don't know why mathcad has to make certain things so difficult.





