Community Tip - When posting, your subject should be specific and summarize your question. Here are some additional tips on asking a great question. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Do you know this curve?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Do you know this curve?
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
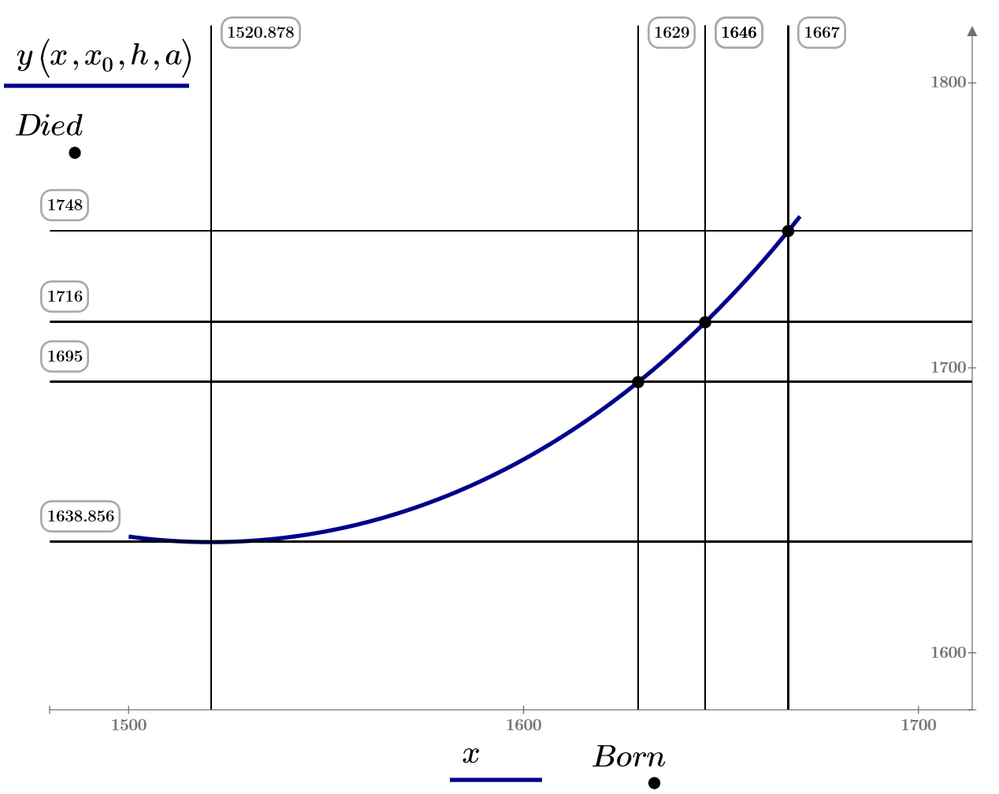
Christiaan Huygens (1629-1695) - Den Haag
Jacob Bernoulli (1655-1705) - Basel
Gottfried Wilhelm von Leibniz (1646-1716) - Leipzig
This is chain line!
Viktor
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
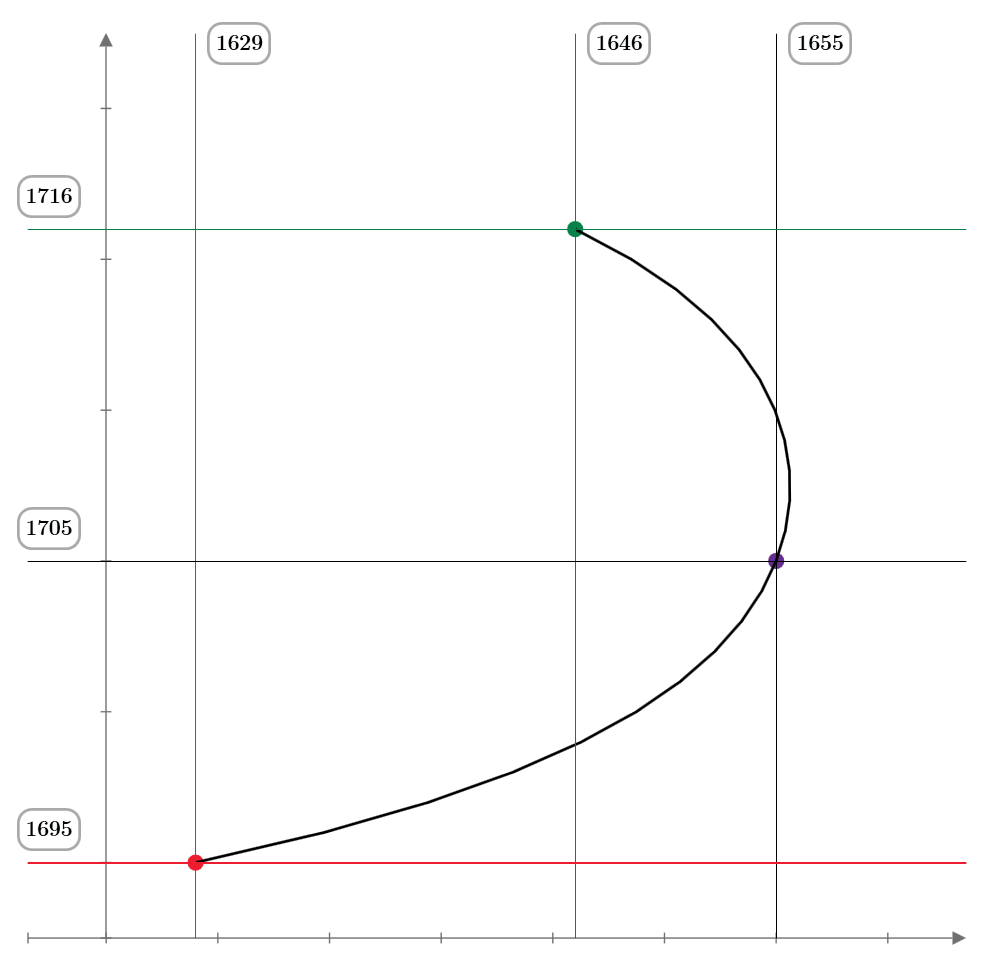
One other view this courve
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
One other view this courve
Sorry!
I confused Bernoulli. There were a lot of them. See please https://en.wikipedia.org/wiki/Bernoulli_family
Another Bernoulli came up with a chain function.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Distance to some location in France...?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry, no!
It is pure Mathematica!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
...curve?!?!?....
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
it's on of the chokes of Valery ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Volker Lehner wrote:
it's on of the chokes of Valery
Was this a Freudian ? ![]() A joke you can choke on?
A joke you can choke on?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
of course i meant joke ![]()
![]()
![]()
![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
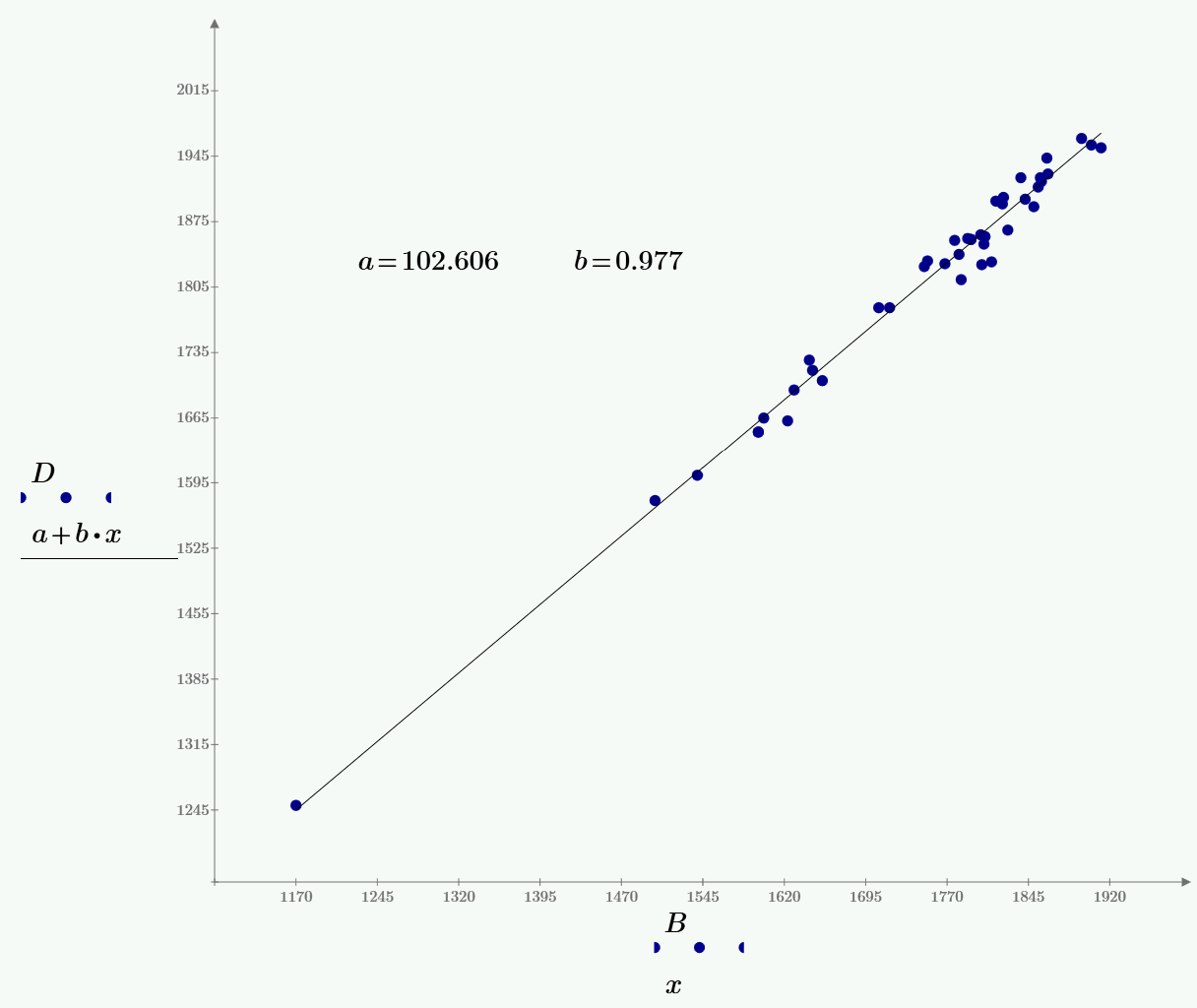
The Joke is continue!
Can you open Prime 3.1 sheet, inserts names and new points of this line!
And better use not YYYY but DD:MM:YYYY
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
F.M. написал(а):
...curve?!?!?....
A function and a curve of this function.
But not Parabola or Hyperbola!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
...My was only a joking statement,.... since in Russian (or Ukrainian) it assumes a very different meaning and has nothing to do with math ...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
F.M. написал(а):
...My was only a joking statement,.... since in Russian (or Ukrainian) it assumes a very different meaning and has nothing to do with math ...
Something about women?
No!
Three men!
One from Haag (with name H...)
Second From Leipzig (with name L...)
and 3-d fron Basel (with name B...)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
... we say ... women with "loose morals" ... in short ... those there .... the who***
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
F.M. написал(а):
... we say ... women with "loose morals" ... in short ... those there .... the who***
In Russian (and Polish) курва (curva) - it is one bad woman.
But my курва connects three men H, L and B, not a bad woman!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Christiaan Huygens (1629-1695) - Den Haag
Jacob Bernoulli (1655-1705) - Basel
Gottfried Wilhelm von Leibniz (1646-1716) - Leipzig
This is chain line!
Viktor
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes!

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
More about this task
https://community.ptc.com/t5/PTC-Mathcad-Blog/Study-28/ba-p/483696