Community Tip - When posting, your subject should be specific and summarize your question. Here are some additional tips on asking a great question. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Does pdesolve assume boundary conditions when they are missing?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Does pdesolve assume boundary conditions when they are missing?
I was working on a problem in another discussion and I noticed something strange about pdesolve: it appears to assume a boundary condition.
The figure below shows the same equation for a fixed bed reactor solved with two sets of boundary conditions. Because the equation is second order in x, there should be two b.c. on x. The solution on the right for c2 only has one, yet the results are nearly identical to the c solution on the left.
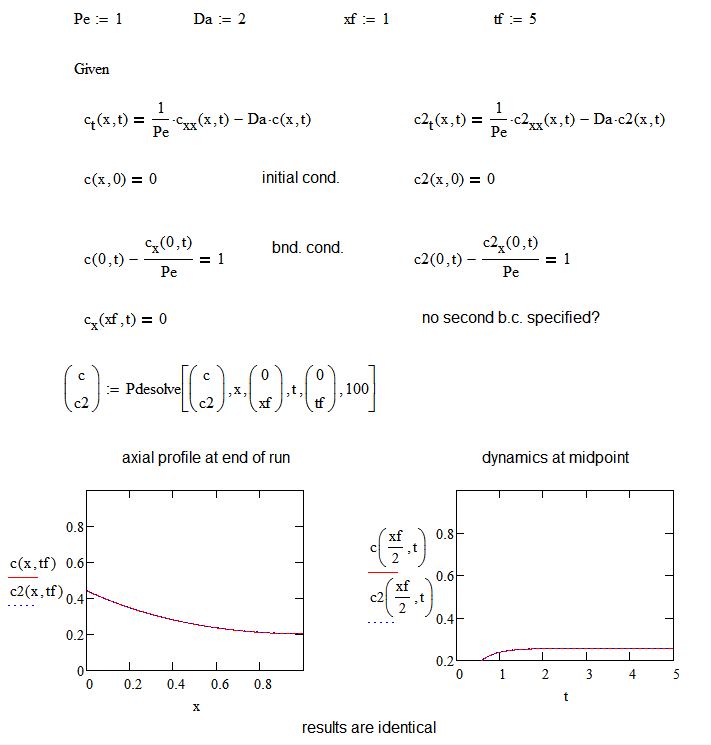
If I change the outlet derivative b.c. for the c system, the results do change. This implies that the second boundary condition is active if supplied.
Also, I have changed the systems so that the first b.c. for both is merely the concentration at x=0. Both systems get solutions that are nearly identical again.
Can anyone confirm my deduction that pdesolve is assuming a missing b.c.?
- Labels:
-
Calculus_Derivatives
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
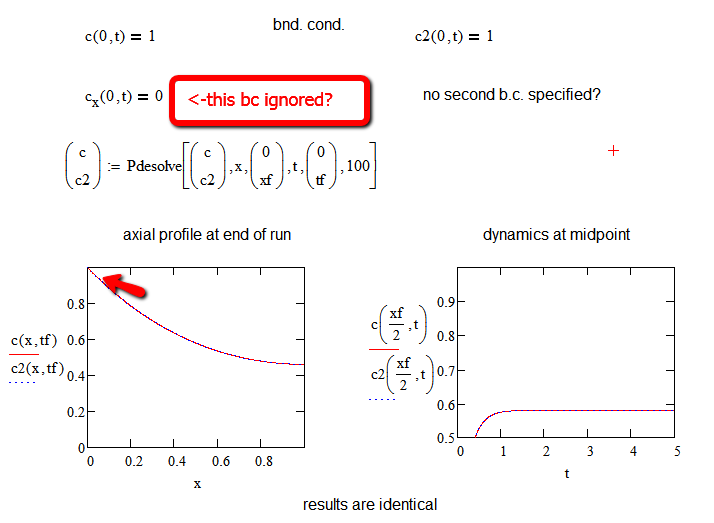
More strange behavior. It looks like pdesolve will ignore a second boundary condition at the inlet in favor of its assumed bc at the exit.
The MC15 file is attached with the values show in this example.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I've found out that pdesolve doesn't discriminate regarding missing b.c.: it set the inlet dc/dz=0 when I had set an exit condition. That makes sense, but I wanted to cover all cases. The supplied missing b.c. is always the derivative=0.
My investigation has convinced me that pdesolve is supplying the missing b.c. I think it would be nice if the documentation mentioned this fact. The documentation in the help file is shown below. In actual operation, pdesolve doesn't allow one boundary to have both b.c. Also, it doesn't give an error when one b.c. is missing.
I suppose this is all meaningless unless a pdesolve replacement appears in Prime in the future.





