- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Doing something wrong in Matcad. What is it?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Doing something wrong in Matcad. What is it?
11/13/17
I hope someone can help me. I am using MathCad 15 Academic (professional?) and have a problem that involves several variables, e.g. x ,y, z, that are implicit functions of a range variable, ϴ = 0, 0.1,…1, e.g. 0 = f(ϴ,x,y,z). I want to obtain explicit functions, e.g. x(ϴ, y), so that I can graph x(ϴ, y) vs ϴ in order to determine if a supremum is at a boundary or interior value of ϴ.
I have several such variables, e.g. y(ϴ,z), which are part of a more complex function, e.g. G(ϴ, x(ϴ, y), y(ϴ,z)), that I want to evaluate in terms of a supremum for ϴ. Using the “find” function in MathCad I have successfully obtained values of x, y, and G, for each of the values of ϴ and manually inserted these into a vector, e.g. x(ϴ, y). However, I have not created a function as I cannot graph x(ϴ, y) against ϴ. Evidently, there is something simple which I am not doing (despite my many attempts). I hope someone can tell me what I should be doing. Thanks. Jim
Solved! Go to Solution.
- Labels:
-
Physics
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@jholmes1 wrote:
Werner, Thank you so much. One question to be sure that I understand you. If I use the first method, with the solve, and assume, then I cannot graph the resulting function of Thata, but if I use the solve block method then I can? I will not be able to try these until later.
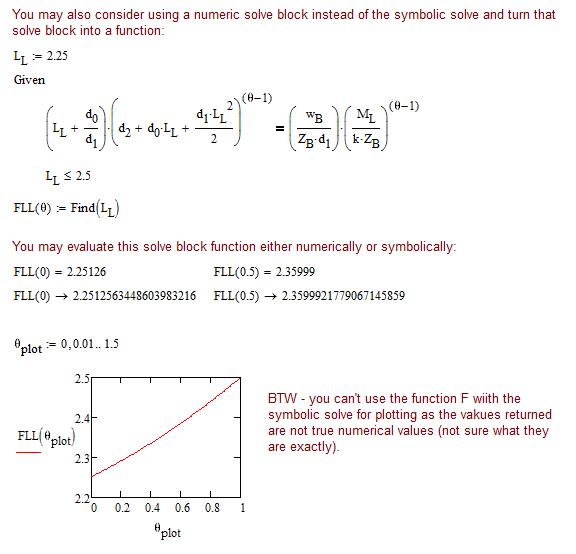
Exactly. The reason is that the function using the symbolic solve command is a bit tricky as the symbolic evaluation is copied inside the function (which is not possible to do in Prime anymore). The result of that kind of function is quite strange and not the same as the result of a normal function.
You may have noticed that that function displays its results in "full" precision like a symbolic result even when evaluated numerically. So the result is still a "symbolic" value and fails in some situations where true numeric values are required as is the case when it comes to plotting.
You are sure better off and on the safe side if you use an ordinary numeric solve block.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Please attach your Mathcad sheet.
You may have to zip it first. A serious bug in this forum prevents direct uploading of Mathcad worksheets for most users. But a .ZIP file can be attached to a posting.
To get the .zip file, use Windows Explorer, select the sheet file, right-mouse click and select "Send to" then "Compressed (.zip) folder". this results in a .zip file containing the worksheet that you can attach.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fred, It almost worked, I believe. Unfortunately, I could solve for specific values of the range variable, but it gemerated 2 values. One of which is not feasable, but I do not know how to specify that. I attach a zip file of my MathCad work sheet. Thanks so much for your help. Jim
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here are some remarks. Hope it helps:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner, Thank you so much. One question to be sure that I understand you. If I use the first method, with the solve, and assume, then I cannot graph the resulting function of Thata, but if I use the solve block method then I can? I will not be able to try these until later.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@jholmes1 wrote:
Werner, Thank you so much. One question to be sure that I understand you. If I use the first method, with the solve, and assume, then I cannot graph the resulting function of Thata, but if I use the solve block method then I can? I will not be able to try these until later.
Exactly. The reason is that the function using the symbolic solve command is a bit tricky as the symbolic evaluation is copied inside the function (which is not possible to do in Prime anymore). The result of that kind of function is quite strange and not the same as the result of a normal function.
You may have noticed that that function displays its results in "full" precision like a symbolic result even when evaluated numerically. So the result is still a "symbolic" value and fails in some situations where true numeric values are required as is the case when it comes to plotting.
You are sure better off and on the safe side if you use an ordinary numeric solve block.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You need to read up on solve blocks. Look for the green.