Community Tip - When posting, your subject should be specific and summarize your question. Here are some additional tips on asking a great question. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Double integreal calculation, unknown error
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Double integreal calculation, unknown error
Hello there,
I have try to calculate a volume of a torus, and for that I use a function of z and two integrals, but I got error "unknown error".
I believe my formula is right, also expression.
You can check attaeched document.
It works in cylindrical coords, but I also have to calculate in cartezian . What I'm doing wrong?
regards, LL
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I believe my formula is right, also expression.
Both integral limits are wrong.
The outer integral has to run from 0 to 80 (R+r) and the the upper limit of the inner integral gets imaginary for values greater than 40 (which is the reason for the error). So replace it by its real part which sets it to zero for values greater than 40 and this happens to be exactyl what is needed. Furthermore you should either use the second value of z or switch the integral limits, but thats just a matter of sign.
You formula will only calculate the volume of the upper half of a quarter of the donut, so you have to multiply it by 8.
If you let the outer integral go from -80 to 80 you get the upper half (you have chosen the positive root for z) of the right half (y>0) torus and have to multiply by 4 therefore.
For better accuracy you should decrease the value of TOL - default is 10^-3 which gets you a slighty different result compared to the "exact" v.boia.
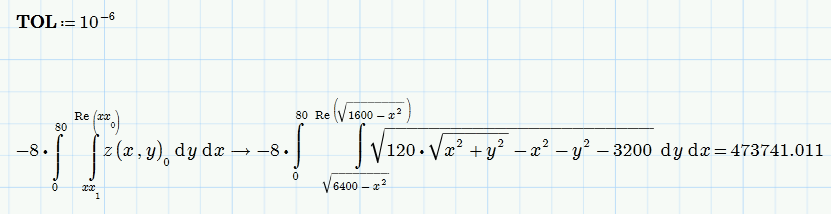
There is no symbolic evaluation necessary:
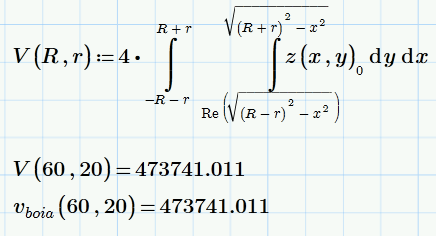
And if you like to use units, too, you have to redifine z(x,y) - best done in a general form using R and r as arguments:
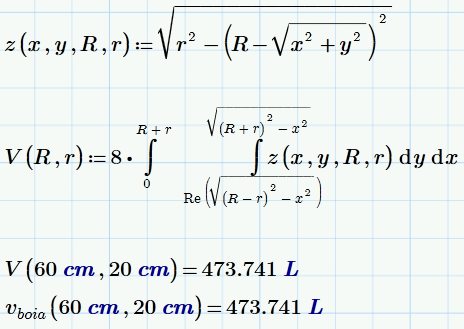
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I believe my formula is right, also expression.
Both integral limits are wrong.
The outer integral has to run from 0 to 80 (R+r) and the the upper limit of the inner integral gets imaginary for values greater than 40 (which is the reason for the error). So replace it by its real part which sets it to zero for values greater than 40 and this happens to be exactyl what is needed. Furthermore you should either use the second value of z or switch the integral limits, but thats just a matter of sign.
You formula will only calculate the volume of the upper half of a quarter of the donut, so you have to multiply it by 8.
If you let the outer integral go from -80 to 80 you get the upper half (you have chosen the positive root for z) of the right half (y>0) torus and have to multiply by 4 therefore.
For better accuracy you should decrease the value of TOL - default is 10^-3 which gets you a slighty different result compared to the "exact" v.boia.
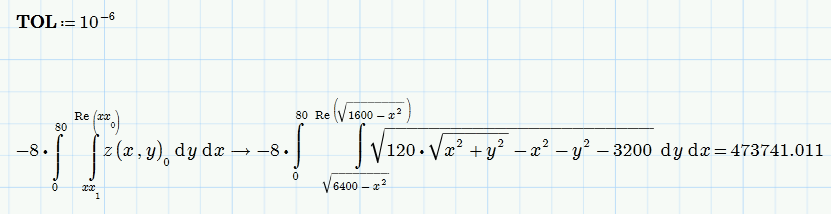
There is no symbolic evaluation necessary:
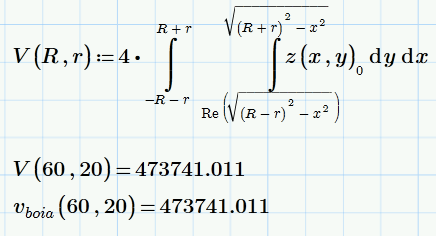
And if you like to use units, too, you have to redifine z(x,y) - best done in a general form using R and r as arguments:
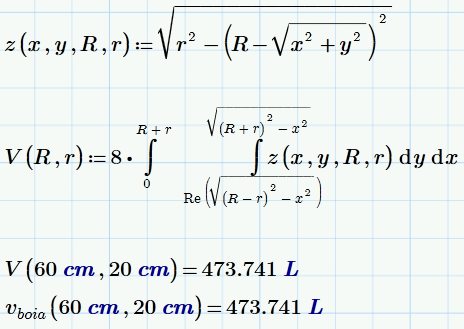
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello WE,
Okay, I just use the real function of square root. And now its fine.
Thank you for your help.
Regards, LL





