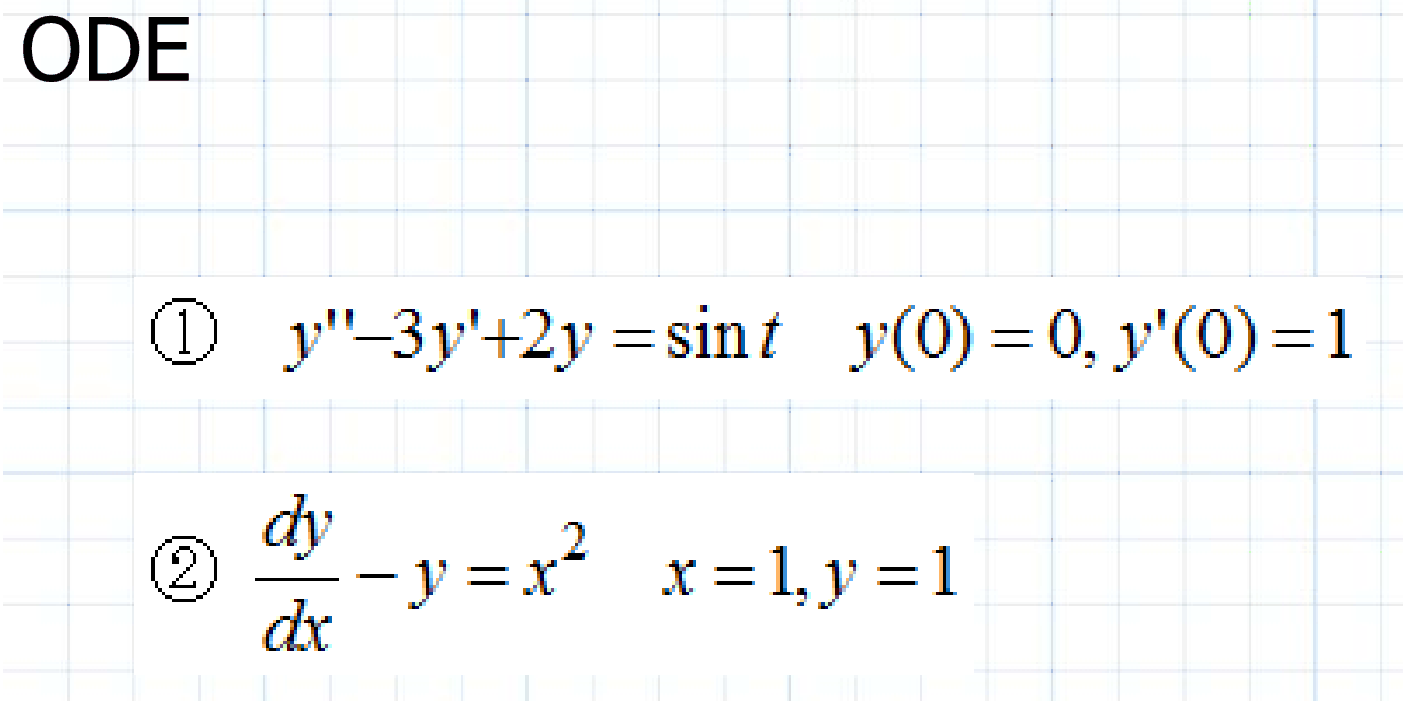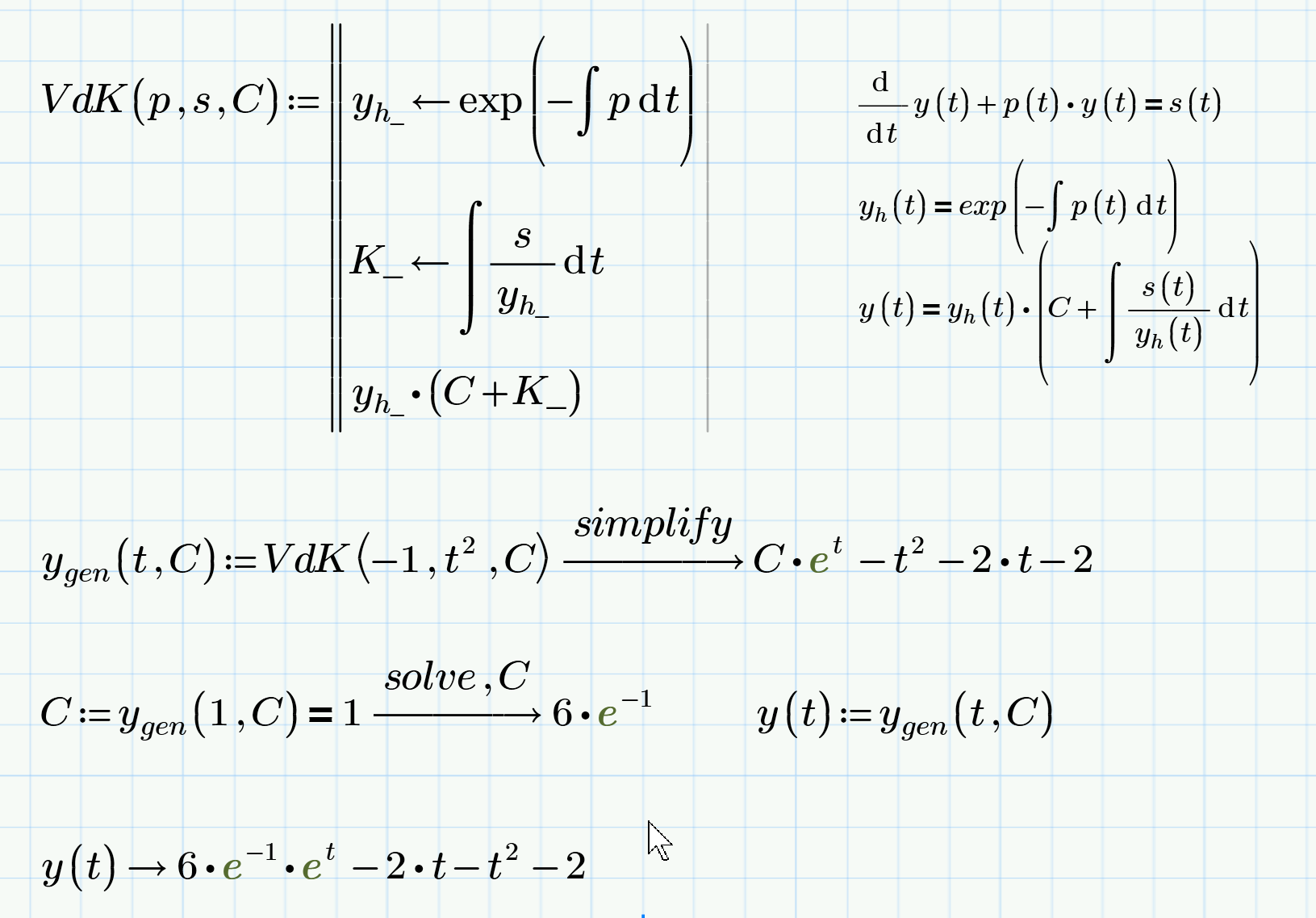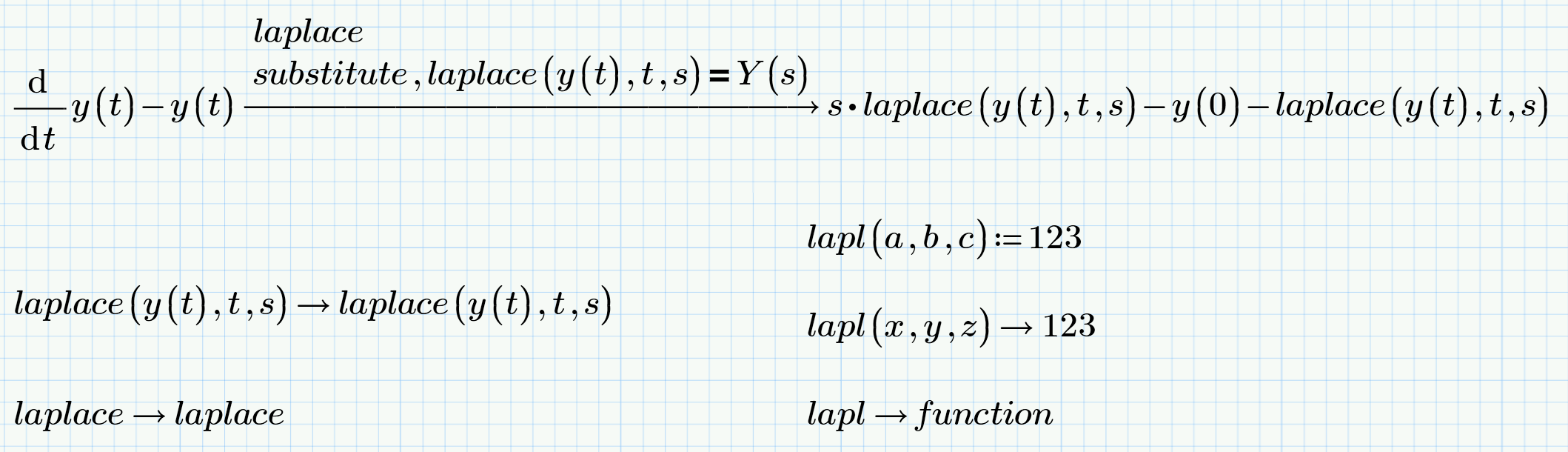Community Tip - You can subscribe to a forum, label or individual post and receive email notifications when someone posts a new topic or reply. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Electric Circuit ODE solving
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Electric Circuit ODE solving
Is their more smart way to solve ODE question No. 2 by Mathcad Prime 4.0?
My answer is attached.
T.Tokoro.
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ttokoro wrote:
Problem 1 can solve only one line.
Is problem 2 also can solve one or two steps?
How about this, using time shifting:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
For the ODE of first order maybe a utility function like this:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Problem 1 can solve only one line.
Is problem 2 also can solve one or two steps?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ttokoro wrote:
Problem 1 can solve only one line.
Is problem 2 also can solve one or two steps?
How about this, using time shifting:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You did NOT do that in one step:
This proves that y1(t) is a solution to ODE1.
This poves that y2(x) is a solution to ODE2.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Luc, you probably know that your MC11 solution will not work in MC15 or Prime.
Using the time shift as in my response above I guess that with MC11 it should be possible to get the solution for ODE2 in one go, too.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sure, I know!. For Mathcad 15 I'm certain.
It was just that I was surprised how far the OP got with solving the 2nd order ODE. Maybe my example could give some idea how it could be done in Prime.
Can you define in Prime:
laplace(f,t):=f(t)->laplace,t
(that is...symbolic ) and have it work like the laplace operator?
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@LucMeekes wrote:
Sure, I know!. For Mathcad 15 I'm certain.
It was just that I was surprised how far the OP got with solving the 2nd order ODE. Maybe my example could give some idea how it could be done in Prime.
Can you define in Prime:
laplace(f,t):=f(t)->laplace,t
(that is...symbolic ) and have it work like the laplace operator?
Luc
No, thats not possible.
When the symbolic laplace is applied to a function y(t) the symbolics return "laplace(y(t),s,t)" as in the good old maple days, but this function is of no value and obviously treated as something special (probably simply a remainder from the Maple time).
Its not possible to use "substitute" to replace "laplace(y(t),s,t)" for something else nor does it help if we define our own function "laplace" with three argument before the symbolic laplace is applied. The two are treated as something completely different. Furthermore "laplace" is even treated by the symbolics like an unknown or undefined function:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator