- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Equation Solving 2.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Equation Solving 2.
Hello, Everyone.
My question :
My question is : Is there an other built-in function for this ?
Thanks in advance for your time and help.
Best Regards.
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Loi Le schrieb:
My question is : Is there an other built-in function for this ?
Yes, you could use a solve block without guess values and evaluate it symbolically. The result however will be the same. The expression for M is too large for Mathcad to display. See attached file.
But I think that you are not really interested in looking at an expression that big - you'd rather want to use it (for whatever). And you can do this in any way you would do if you could see it,
You have to assign the evaluation to a variable, a vector (or Matrix, if there are more than one solution) and may symbolically show the single elements. All but the solution for M will display.
See the attached file for more information.
WE

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Nice idea to use substitution to shorten the expression.
Maybe it would be more comfortable to let Mathcad do the work.
On the other side nothing would be comfortable with that sort of expressions, I suppose. So I have chosen a more simpler example to demonstrate. You may apply the same method using the solve block, of course.
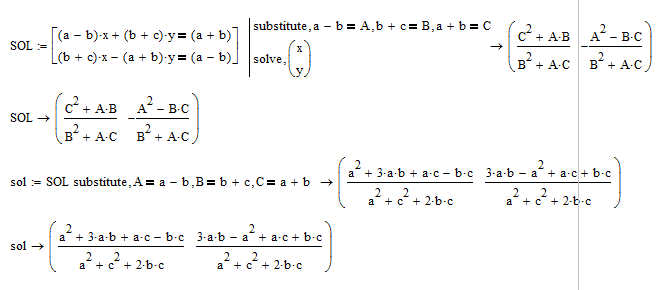
I can not think of any way to avoid having to retype the substitution (third expression, resubstitution)
WE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello Everyone again,
And I have a related question :
Thanks in advance for your time and help.
Best Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Because of the special way your equations are constructed you could solve that system "manually" by substituting the first equ in the second, solve for J, substitute in third, etc. If you don't insist on simplfying N or factoring M, all solutions can be "seen", although I wouldn't like them. Guess Mathcad is somewhat at its limits, concerning its abilty to display large expressions.
Another idea would be that you try Prime. I don't like Prime, but as I understand, the problem of large expressions seemed to be solved there via extendable regions.
No clue what the hell you are trying to do here at all - maybe you could give us a hint.
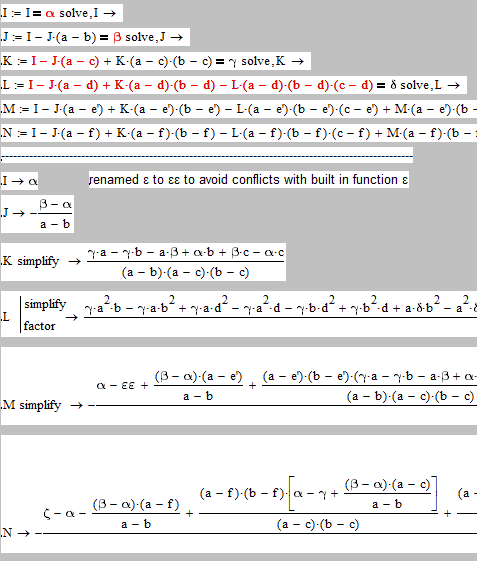
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Loi Le schrieb:
Thanks for your hint, the above, Werner. And doing manually the following similar one :Best Regards.
Glad it was of use for you.
Looking at your solutions and the symmetry in it I would guess you could calculate them directly without using the original equations and withou solve. Probably best using recursion, as the n-th solution is (solution (n-1) - [solution (n-1) with every index substituted for the next one])/(a[1-1[n).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thats it what I meant. See attached worksheet for a possibility to resubstitute to A,B,C, etc.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
...file
Thought Loi would like to do it himself in the worksheet he(?) is working on. 🙂
If he needs my sheet I think he will give me a shout.
Hopefully not a "related" question with eight or more variables.
@Loi: I don't know from what problem your variables come from, but it seems you are running out of alphabets. You may consider using literal indices or even vectors, if possible. The equations you provide seem to follow a rule. Maybe you could write them more compact by using vector operations and/or summation sign. Just came to my mind.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK Loi,
see attached what I meant by using vectors. I think these are the equations you are dealing with.
Its almost automatic, but I dont know what can be done to automate the vector at the solve command.
You may have to delete the "simplify" at the solve command when increasing N.
Perhaps someone else has an idea - see screenshots below or attached worksheet.
You will run into the same problems with Mathcad not being able to show the result.
You may work with an automatic substitution (a[j] - a[n]) --> A[10*j+n] or something similar to make the expressions shorter - see attached sheet.

Does anyone know why the follwing two expressions don't work and how one could make the solve to work withou manual intervention for arbitrary N?

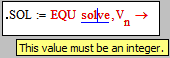
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The solution your problem is beyond my capabilities. Mathcad studying only for 3 months.Therefore, you can not help![]()
PS. (google translator is suc*s)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'm not sure if a solution to this problem exists. The coexistence of the numeric and symbolic processor is not always smooth and peaceful.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Many thanks for the equivalence one, Werner.
Best Regards.





