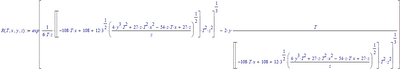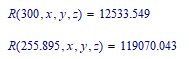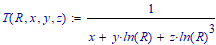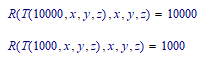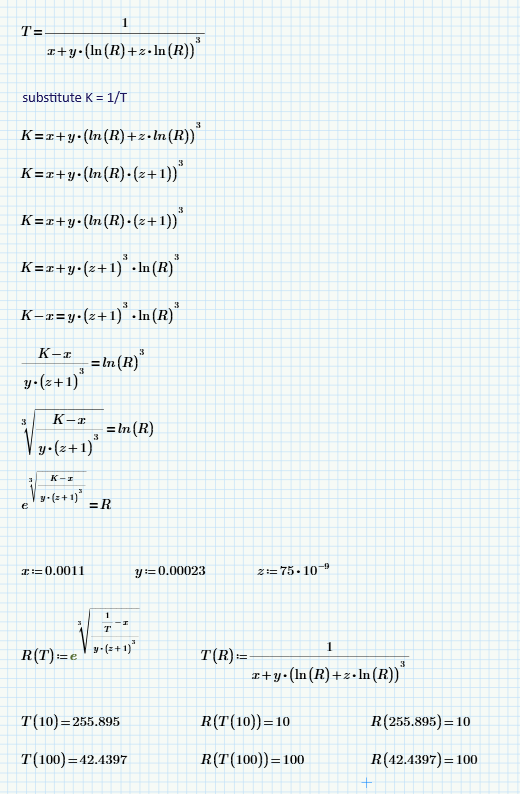Community Tip - If community subscription notifications are filling up your inbox you can set up a daily digest and get all your notifications in a single email. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Equation not solving in Mathcad Prime
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Equation not solving in Mathcad Prime
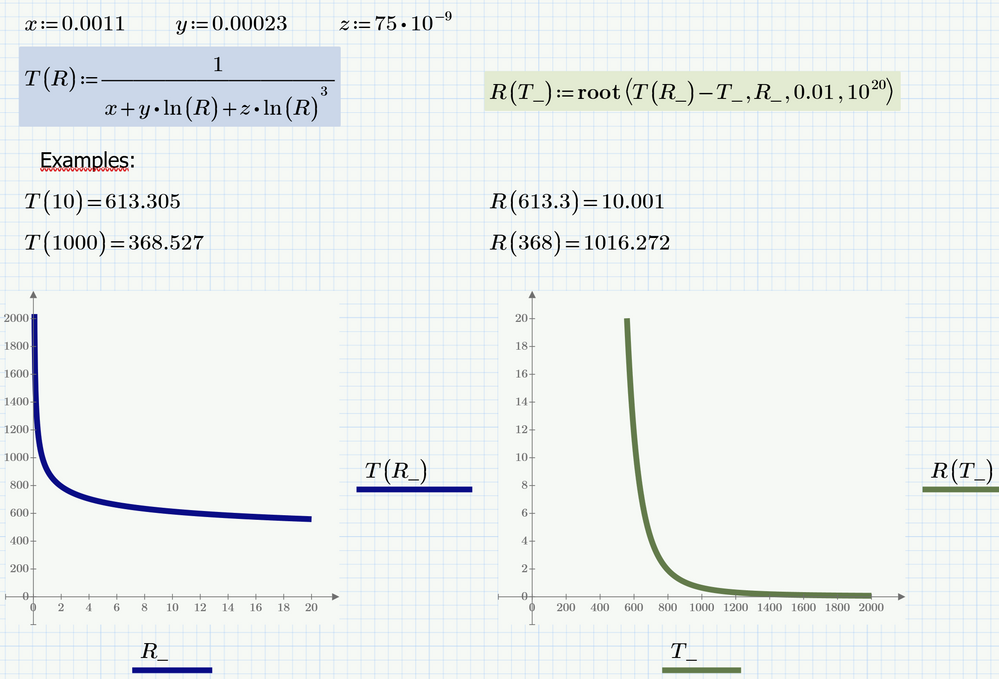
- T(R) -> Temperature is a function of resistance. Therefore, if I want to find out a Temperature at a specific Resistance you can plug in a value of 10 kohms and get a corresponding value of Temperature -> degrees C. -> This is Given.
- 3 Constants are provided and fixed. They are givens.
Goal -> Rewrite T(R) Equations so that Resistance is a function of Temperature -> i.e. R(T) := ???????
I would like the equation in a format where I plug in a temperature and get a corresponding resistance.
Again I am looking to rewrite T(R) as R(T):=
Can somebody help
Solved! Go to Solution.
- Labels:
-
Mathcad Usage
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Note that, due to the third power, you get three possible solutions of R for every value of T.
So here is the general solution:
With x, y and z defined numerically, you can have:
Only the first of the three solutions gives a real answer (the other two are complex).
Assuming you don't want the complex answers, you can set:
which yields:
and of course, with:
you get:
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You may use a solve block or the "root" function.
The names T_ and R_ were chosen for the function arguments (and later for the abscissa variables) to avoid conflicts with the name of the two functions. Feel free to change them as you think is appropriate.
P6 sheet attached
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Werner,
Does the OP's cube enclose the other ln(R) expression, as well?
(I think the question also asked for a rewrite. I'm guessing that didn't mean "solve by any means that works"?)
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@StuartBruff wrote:
Hi Werner,
Does the OP's cube enclose the other ln(R) expression, as well?
Forget the above. You are correct. It's my eyes that are the problem. Definitely time for new glasses. And there goes my new laptop fund. 😞
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As partial penance for my earlier faux pas, here's a Prime 7 symbolic solution that seems to agree with Luc's but gives a slightly different approach that is, in principle, solvable by hand using the standard cubic solution.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So it is symbolically solvable with Prime as well. Can Prime do it from the original equation as well?
(I support your argument "for example, copying the wrong expressions, and failing to update the function definition after any changes to the original expression.", but you already used such an error prone action by copying the expression to the definition of rrexp...)
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@LucMeekes wrote:
So it is symbolically solvable with Prime as well. Can Prime do it from the original equation as well?
It doesn't look like it, Luc. I got the standard "no solution was found" error message.
(I support your argument "for example, copying the wrong expressions, and failing to update the function definition after any changes to the original expression.", but you already used such an error prone action by copying the expression to the definition of rrexp...)
Welcome to the wonderful world of "Do as I say, not as I do". 🙂
It's actually just an exercise in risk vs performance management. The symbolic processor (SP) is rather tardy on my PC and it was expedient to gamble on correct copy&paste for a one-time example. Given that the SP is so reluctant to find a direct solution, any other method requires some form of manual manipulation, thus introducing risk, anyway. The attached worksheet goes some way towards being a better example.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Note that, due to the third power, you get three possible solutions of R for every value of T.
So here is the general solution:
With x, y and z defined numerically, you can have:
Only the first of the three solutions gives a real answer (the other two are complex).
Assuming you don't want the complex answers, you can set:
which yields:
and of course, with:
you get:
Success!
Luc