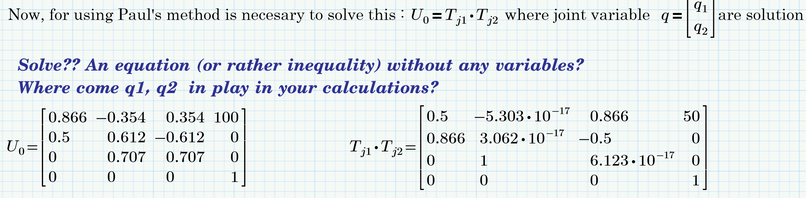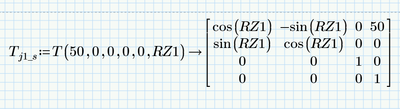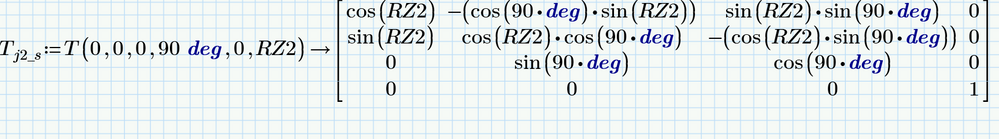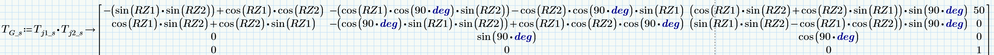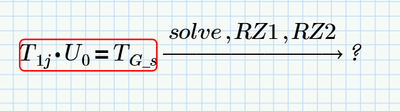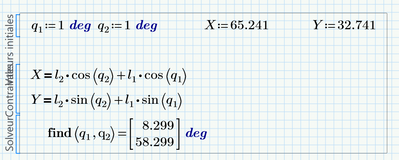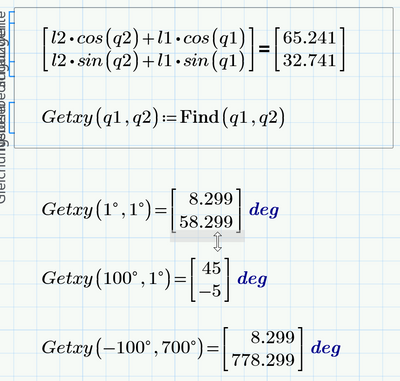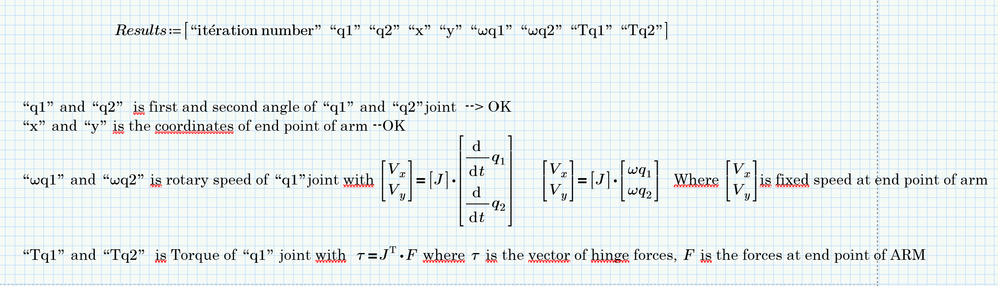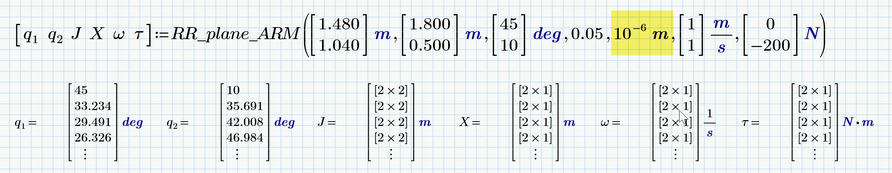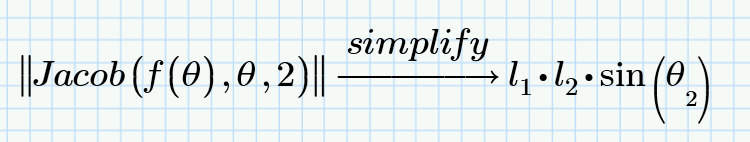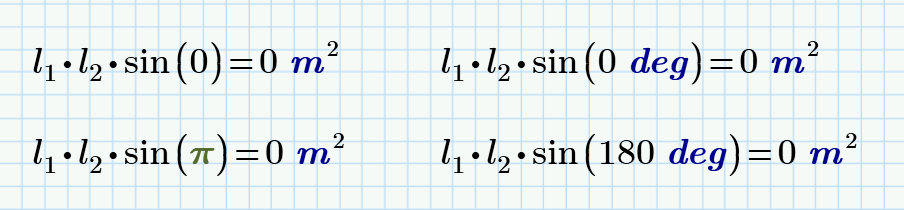Community Tip - You can Bookmark boards, posts or articles that you'd like to access again easily! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Equation solving
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Equation solving
Hi community
I don't know how to use prime to find solutions to a robotic problem this problem is based on matrix calculus for a serial type robot it is easy to determine the direct geometry, i.e. to express the generalized coordinates according to the joint coordinates The difficulty is to solve the inverse geometry, that is to say determine the coordinates of the joints according to the generalized coordinates usually this uses Paul's iterative method I don't know how to solve these equations with Mathcad see the attached sheet
Solved! Go to Solution.
- Labels:
-
Mechanical_Engineering
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Prime does not have a "do ... while" or "REPEAT ... UNTIL" kind of loop which would be more appropriate for this task.
Nonetheless here a shorter version which avoids doubling the calculation of X.
It makes one additional iteration step at the end, though!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
From your description it is not clear to me how q is used in producing Uo. That makes it difficult to find q from a given Uo.
Here's your file in Prime 6, for a broader audience.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
the joint variable q is (in this example) RZ1 and RZ2
to show the variables, is necessary to rewrite TG with symbolic parameter
symbolic TJ1:
symbolic TJ2:
Symbolic TG
And finally
sorry it was true that it was not clear
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The reason for the "solve" command failing could be because you end up with much more single equations compared to just two unknowns.
Furthermore the symbolics doesn't know "deg". You may try to define deg:=pi/180 at the top of the sheet (deg must be labelled as unit) or you use radians throughout.
And I just notice that you demand the impossible:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
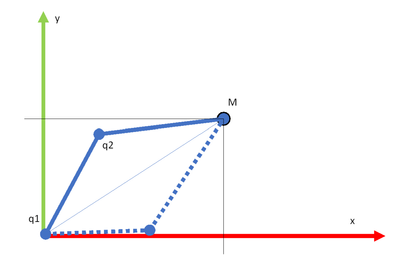
sorry for my bad explanation I will try to resume more simply with the example of a planar robot
The robot is in solid line
It is easy to determine Direct Geometrical Model
Now, i want to find Inverse Geometrical Model
q=(Fx)
it is obvious on the drawing that several solutions are possible
It is now that the difficulty appears. How to calculate joint variables based on generalized coordinates with Prime I am not necessarily looking for a symbolic solution, I have heard that it is possible to solve this with Newton's numerical method. But I don't know that. Even if this method will produce only one of the possible solutions, maybe it will be possible to refine the algorithm with bounds
This example is simple, but if we add a new segment to the robot it is much more complicated
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
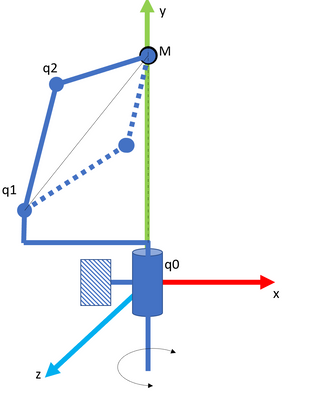
For example:
we add a pivot on a spatial model.
It is clear that M is invariant for all values of q0 (if q1,q2 are fixed)
so there are many solutions for the joint variables for a single position of M It is now that we could say to the algorithm: Consider Pi/2<q0<Pi for example
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The problem is that you never set up a clear system with equations where your unknowns are clearly seen.
In the example you just posted I assume that the last line, the 2 x 1 matrix M is given, you know that is must be created by a matrix of the type we see in last but one line (with l1 and l2 as known constants and q1 and q2 as variables to calculate.
Here the math is clear as you have two equations and two variables to solve for.
But in your original example, where I , as I understood it, noted that you demand the impossible (1 is never equal to sqrt 2 /2), it looks like you have 16 equations but still only 2 unknowns.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In the simple example we seek the coordinates in X and Y of the point M according to the geometry l1 and l2 (the constants) and the joint variables q1 , q2
Yes the original model is wrong, I wrote it on paper and I must have made a mistake in the transport, and in the application of the method. That's why I'm starting from a simpler example to correct my model step by step
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In the simple example, i find X,Y with blocksolve
here it is clear that for the generalized coordinates of M(X,Y) BlockSolve gives the joint variables q1,q2
But can Blocksolve provide all the solutions?
here the value in the first calculus
q1=45°
q2=-5°
Are there other ways than going through blocksolve?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I also tried and I was surprised that the symbolics is not able to find a solution, not even when provided with the exact symbolic values.
And yes, I also noticed that a solve block is able to provide a solution
And, no, a numeric solve block will only return one specific numeric solution. If the system has more than one solution it depends on the guess values which one you get.
Apart from choosing different guess values you can also add additional constraints to control the output
Sometimes with unexpected results 😉
According different guess value - you can also turn the solve block into a funciton with the guess values as its arguments.
That way you can quickly experiment with different guess values
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello everyone I'm coming back to an old message, no need to make a new one
It's the same robotics problem as before.
of course the given solutions work, but from an automatic point of view I would like to use an iterative method
I can apply this method by hand, but I have difficulty coding it in a program
Can anyone help me
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
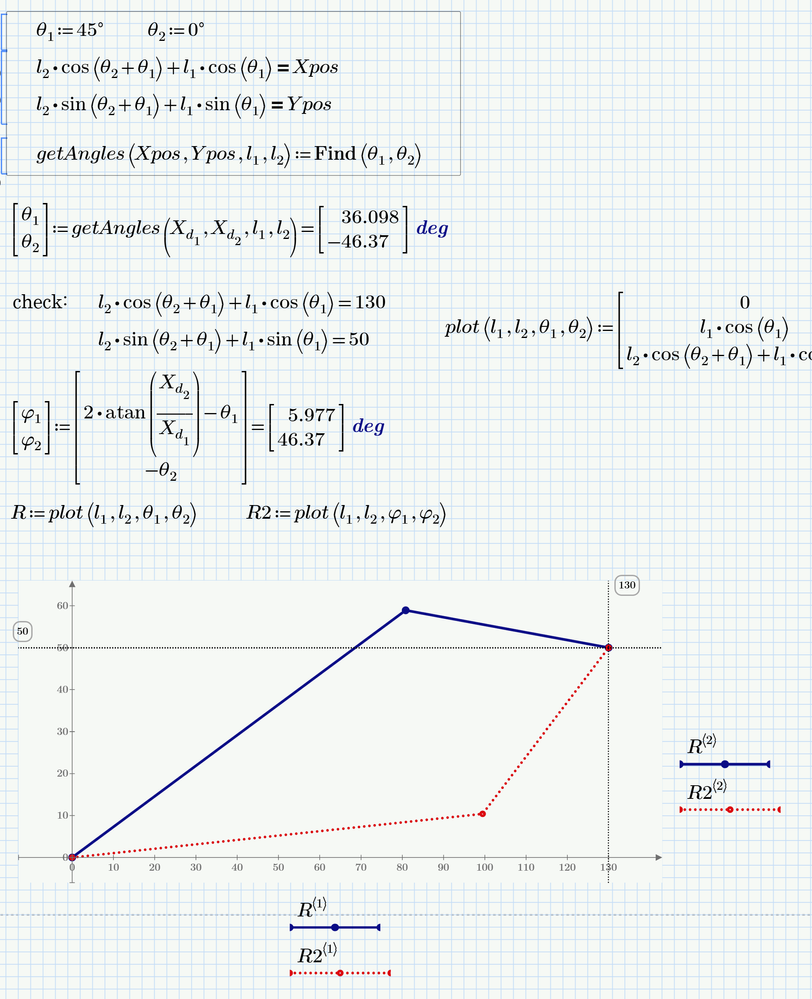
I am not sure about the iteration algorithm you would like to program, but I guess it sure would help to turn all the calculations into function of the variables you would like to vary.
But why not rely on the algorithms built into Prime?
You may turn a solve block into a function of the target coordinates X.d and maybe also of the arm lengths l.1, l.2.
And for the second solution you may calculate it based on the first one as shown in the picture:
You then could use this function multiple times in your sheet for different targets and maybe also different robot arm lengths and you may also use units
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I try it:
I know there are errors in this program but it's a start
there are 3 reasons
1/ to download this into a microcontroller I must not use a Prime function
2/this algorithm makes it possible to determine the inverse model with a unique solution for each displacement
3/the Jacobian calculation makes it possible to find the static forces directly (for calculate joint motor)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I therefore calculate step by step the path to the arrival position of the arm
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'm trying to understand how "while" it works
while i>3 is for example
in reality, while must run until convergence...
But already at this stage it is not working. I must be able to display all the Jacobian matrices for each calculation step
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I don't see what you are actually trying to do, so just a few remarks.
Why do you define X and J as nested matrices? (a 2x1 vector as sole element of a 1x1 matrix).
Why is dX a 1x1 matrix? Isn't it supposed to be a simple scalar (matrix determinant)?
Your while loop runs as long as i is greater than 3. And you increase i in that loop. So once you enter the loop it will run endless!
Fortunately(!?) when you come to that loop, i has the value 1 and so the loop is never entered. So dq remains undefined and I guess your program therefore returns the simple value 0.
What was the problem with the first program you posted? There you used "while (1) " as an endless loop on purpose and breaked out of it using the "break" command.
The condition for break looks a bit strange to me. Should it stop when dq.c[i is near zero?
So that would be something like "if |dq.c[i| < 10^-8 ...".
P.S.: It may be easier to help with the next release of your program if you also attach your worksheet.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
From what I understood so far you might be looking for something like this
(or do you really need all the intermediate J matrices and dX, dq and q vectors from all iteration steps?).
Prime 9 file attached
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Prime does not have a "do ... while" or "REPEAT ... UNTIL" kind of loop which would be more appropriate for this task.
Nonetheless here a shorter version which avoids doubling the calculation of X.
It makes one additional iteration step at the end, though!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Werner
I will look into this in detail
But is necessary to calculate intermediate matrices
For example, i want to need check the determining of J, because if this matrix is not invertible i found a singularity position for example when the segments are aligned
And i use J for calculate static forces for all position of the path .
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
another interest is to make a txt file result:
for example:
q1.txt :with all value of q1 angle
q2.txt : with all value of q2 angle
it's easy if we obtain a matrix result (With this file is possible to drive a virtual servo motor in PTC CREO motion , and is possible to simulate the mechanical arm)
In fact my objective is to obtain a results matrix for each iteration (
this will create the basis for coding on a python microcontroller for example
Werner, thank you again for your superb example program
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If J is not invertible the whole program would fail at the calculation of dq and you won't get any result from it at all.
One option could be that we check if J is invertible and if its not the program stops and returns the values calculated so far.
Which values would you need as an output. All matrices J, all angles theta 1 and theta2 - anything else?
Actually it would suffice to return only the vectors of the two angles as you could calculate J, X, etc. from them anyway.
Here is my last program, modified to return the vectors of angles and J matrices.
The superfluous extra iteration step of the previous function is now suppressed (the if-statement at the end) and in case the calculation of the next set of angles fails (because of an not invertible matrix J) the program stops, returns the values calculated so far and adds a "NaN" as the last value in each of the returned vectors. So the angles and the corresponded not invertible matrix J are the last but one values in the returned vectors.
You may create the text files with the angle values either using the WRITECSV() function or using WRITETEXT().
Prime 9 sheet attached
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Wow 🤗
I don't understand completely your code ...
But , Yes! if det(J)=0 the movemet is not possible
I'm thinking 2 ways
- locally modify the precision to pass through this singular point
- modify the trajectory vector to shift by an arbitrary value to avoid this point
But what you are proposing is already wonderful.
In fact, for output is what is interesting:
- q1 angle
- q2 angle
- first joint position (x,y)
- second joint position (x,y)
- speed of joint (wq1, wq2) with [Vx,Vx]=J*[wq1,wq2] Vx,Vy are fixed (the speed of end arm)
- Torque of joint(Tq1,Tq2) with tau=Jtranspose*F F are the forces at the end point of arm
- Arm stiffness for position Kext=(Jinv)Transpose*K*Jinv
Great !
You have my complete gratitude
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Maybe this quick hack can solve the problem with |J|=0.
In case this happens we go back one step and use epsilon/2 for the next step.
After that the given value of epsilon is used again and so I guess this should pass through that point. If thats true, the try...on error at the end would no longer be necessary .
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK
perhaps it is by increasing epsilon that we have a greater chance of passing through the singularity ?
for the rest, I added the necessary data, it's great
there are still unit problems
in this results matrix
m/s is wrong , rpm is correct (this is angular speed)
N is Wrong, Nm is correct (this is a Torque)
I think I'm going to rewrite by removing all the units 🤔
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@XDN wrote:
OK
perhaps it is by increasing epsilon that we have a greater chance of passing through the singularity ?
You have to give it a try and use something like 1.1*epsilon instead of the epsilon/2 I used.
Don't have any test data where the inverse would fail. Just thought that making half a step backwards and then a full step forward again may do the trick, but could not test it.
there are still unit problems
in this results matrix
m/s is wrong , rpm is correct (this is angular speed)
N is Wrong, Nm is correct (this is a Torque)
I think I'm going to rewrite by removing all the units 🤔
You did not attach your worksheet and your second screenshot is cut off and does not show if you provided a correct length unit for the first function argument (arm lengths) when you called the function. Providing unit-less values would explain the wrong units you experience.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry
i forget to attached worksheet in my previous post
here for unit problem
Unit are not compatible,
I think it's because of the Jacobian ??
maybe it's simpler to remove them and freeze the input units in usual mechanics: MMNKS
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The parameter "prec" is a threshold for the difference between the current and the desired position as must be a length.
As an alternative, if you want "prec" to stay unitless, you have to change the program accordingly and divide by the desired length unit
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
of course ! sorry I didn't see it, I'm stupid
thanks ! it's good
next week a make a test to see the behavior on a singularity, for this , for this I am trying to solve J=0