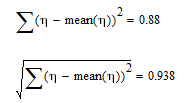Community Tip - You can change your system assigned username to something more personal in your community settings. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Error fitting of a slope in mathcad
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Error fitting of a slope in mathcad
Hello,
I have a submission tomorrow and I need to calculate the error in my calculated value of the intercept c and gradient m.
I have used both the mathcad function and the manual version of it to fit my data points to a line (finding alpha and beta for a langmuir isotherm) and now just need to use the error values for my measurements to get the final absolute error in the slope and the intercept. Can anybody help?
The data set sigma corresponds to the error in eta, the excess amount adsorbed.
Cheers
Fraser
- Labels:
-
Statistics_Analysis
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Use stderr(P,P.n)=
Via help you can access a helpul quicksheet about Linear Regression.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for the quick response Werner,
I have already tried this however I want to know the error attributed to the propagation of the uncertainties in my values of eta.
Do you have any idea how to do this mathetmatically?
Also I have calculated errors for another part of the paper, however they are errors in a value of x. I have plotted x against a varying y and don't seem to be able to add error bars that represent the errors in the value of x; how would I go about doing this? See attached.
Cheers
Fraser
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have already tried this however I want to know the error attributed to the propagation of the uncertainties in my values of eta.
I am not sure what exactly this error should measure and how you would define it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The values used to calculate the intercept and slope of the line are gathered from a simulation and as such each data point has an individual uncertainty attributed to it. I would like to correlate these uncertainties to get the maximum error in the calculated values of y-intercept and gradient.
Is this possible analytically?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As I understand you just want to know how you values of eta influence the aberration of (P; Pn) from a perfect straight line!?
You get a straight line if you vector eta consists of numers all equal.
You you have to set up a measure for the aberration of a vector from a constant vector.
Maybe something like this???