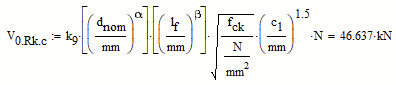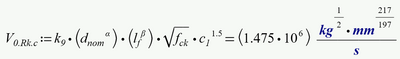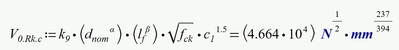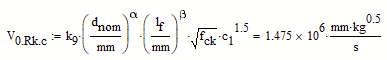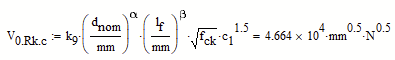Error in MathCAD

[KS_9993416]

Hi,

First post here. i am trying to compute the following equation but unsure of what the error message is meaning and how to rectify. I have included the equation from the Eurocode in the screen shot.

Any help is much appreciated. 

[StuartBruff]

Hi,

I suspect that you have fallen foul of what is known as "Static Type Checking" in Mathcad versions 12 to 15.    Mathcad's static type checking looks for potential unit errors at "compile" time not "run" time.   The idea is to catch unit errors before an expression is evaluated (which may take a long time).   In this case, Mathcad sees a variable as an exponent.   Exponents must be a unitless value, and Mathcad can't exclude the possibility that someone may change the variable to have units.   So, .... Mathcad's static type checker calls foul and won't let the calculation proceed.    The simplest solution is to remove the units from lf purely for the exponentiation and put them back again elsewhere in the expression.

As a matter of Community courtesy, it's good form to post the actual worksheet, or some part of that allows somebody else to see the problem.   It's time-consuming for others to retype an image into Mathcad, especially if they have to guess at missing functions or variable values.  It can also be difficult to spot an error in an image, as there are potential errors that aren't easily distinguishable from a screenshot (for example, putting a subscript after a variable name rather than a matrix index - a very common error).

Cheers,

Stuart

[KS_9993416]

Thanks for your swift and concise reply Stuart. When copied elsewhere, the dnom also flags up as an error so I think the work around is as you have suggested. 

I have attached a section of the file for clarity.

[StuartBruff]

No worries.

Given you know the units, it's fairly simple just divide lf by mm and then multiply lf^β by mm.  More generally, you could use the, I think, SIUnitsOf function to get the correct units where some uncertainty exists about whether the vale was input in metres, mm or cm.

Cheers,

Suart

[Werner_E]

Stuart already explained the cause of the problem - SUC (static unit checking).

Real Mathcad is far superior compared to Prime, but one advantage of Prime is that it does not use SUC. So your sheet works OK there after being converted to Prime format:

or

But are you sure that you really want to see those units for V? Guess no.

So Stuarts advice to remove the units seems to be the way to go. At least you have to remove them for the two critical expressions

or

Which unit is expected for V?

[KS_9993416]

Morning Werner,

The expected units for V would be newtons (N) or kilonewtons (kN).

Thanks,

Kyle 

[Werner_E · Accepted solution]

---

@KS_9993416 wrote:

Morning Werner,

The expected units for V would be newtons (N) or kilonewtons (kN).

Thanks,

Kyle 

---

Thats obviously not the result you get when using your formula with units. So its an empirical formula which means that you'll have to use it with the numbers but without any units anyway. This is done in MC by dividing each variable by the unit which the empirical formula demands (as can be seen with the two variables I divided by mm).  You may add the desired unit N at the end of the expression.

Maybe that way:

[StuartBruff]

---

@Werner_E wrote:

Real Mathcad is far superior compared to Prime, but one advantage of Prime is that it does not use SUC. So your sheet works OK there after being converted to Prime format:

or

But are you sure that you really want to see those units for V? Guess no.

Which unit is expected for V?

---

I am still of the opinion that the way we use units with non-linear mathematical expressions is wrong.  IMO, literally taking powers of units is simplistic and ignores (or beats into submission) the underlying physics. 

If x is a dimensioned quantity xv⋅xu and a is a scalar, I'd regard x^a as being (xv^a)⋅xu, that is as a transformation of the quantity's value, not its dimension. 

If for example, one wishes to square a value, then the result would be xv^2⋅xu, not xv^2⋅xu^2.  The latter is based on an underlying and common assumption that the result should be a 2-dimensional value (ie, a square measure - my view is that the problem determines the quantity dimension (consider an object dropping from rest at a zero reference point). 

It would clear up a lot of problems dealing with such things as trig and exponential functions, and - of particular value(!) - do away with the need to treat angles as quantities of dimension 1 (ie, dimensionless).

Stuart

[Werner_E]

The problem would be what the "quantity's value" exactly is. Whats the quantity's value of 5 km ? Is it 5 because I use km when defining the quantity or is it 5000, thinking of the SI unit or is it 500000 because I use CGS or should we use approx. 16404.2 thinking of U.S. unit system and feet as length unit.

Squaring the full quantity (value and unit) would give a consistent equal area in all cases.

But of course taking a physical quantity to the power of 3.14159 possibly makes no sense wrt the underlying physics. A formula using an expression like this must be considered empirical and it definitely must state with respect to which unit the quantities value should be used. Using mm and N in my last answer above was just an educated guess as these are the units the OP used when defining his variables.

[KS_9993416]

Thank you Stuart and Werner..... Lifesavers. 

Kyle