Estimating the delay between two signals with noise

[ClaudioPedrazzi]

Hi everyone!

This can be a very simple question for those of you that are expert in signal processing.

Suppose I have two time series y1(i) and y2(i) corresponding to two sensors, affected with noise and measurements errors. Known of course is also x(i), the times of the measurements. It can be assumed that the sampling frequency fs is constant, so that x(i)=(1/fs)*i.

Is there a simple way to estimate mathematically / statistically the time delay (if one exists) between the two measures? For example the "human eye" could see that one signal, if shifted a certain Delta-x, pretty well correlates the other one.  

Is it possible, even if the two signals have different numerical magnitudes (say, the second signal is not only delayed but also weaker and maybe with a different constant term)

Somehow I believe this should be possible using the correl(y1,y2) function but some quick tests that I made do not seem to work.

Thanks a lot in advance!

Best regards

Claudio

[LucMeekes]

I assume you would want to set a threshold, and when the signal 'reliably' crosses that threshold an event is detected. Then the time difference between events on y1 and y2 would be the delay.

Did you already try smoothing the y/t signals before threshold detection?

Mathcad has several smoothing functions.

Success!

Luc

[ClaudioPedrazzi]

Hi Luc, happy to "see" you again!

Well, I made some detrending and smoothing, but I was hoping in some kind of "wonderfunction" based on correlation plots, that would have a peak in the proximity of the best estimated delay.

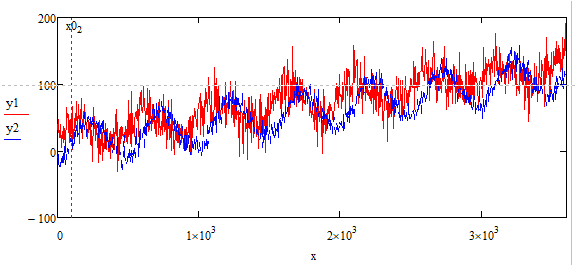
The signal has oscillations in it (imagine two sinuses, hopefully with the same frequency added to a constant value and with much noise). And I have many periods available, and it is not a single frequency, it is more a broadband signal. Something similar to this (but this is a test plot, not the real signals, they are more random).

Hope this can explain my question a little better. By the way in this example the delay between the sinuses is x=100, but the correlation function does not show anything special (at least to my untrained eye):

Thanks again

Regards

Claudio

[Fred_Kohlhepp]

If the signals are periodic, measuring the same wave form from two different locations, then taking the FFT of each signal and comparing the phases might shed some light.

[-MFra- · Accepted solution]

Hi,

I think that if the signals (for example two random processes) are sampled at the same instants, the sample sequences are also produced simultaneously although with a delay. If viewing the two sequences with an oscilloscope, there is a small delay with respect to each other, it means that either they are placed at different distances from the processor or on the connection line with the processor of one of them, there is a system that makes it delay (a buffer or a logic gate is sufficient to generate a delay of a few nanoseconds). One way of calculating the delay (lag) (thanks to Mathcad E-Book: "Signal Processing") is to use the function lcorr as you can see here below:

[ClaudioPedrazzi]

Hi MFra,

and thanks a lot! this is about what I was hoping to be possible with signal processing. By the way, to provide physical background. The signals can be imagined as measures in two different positions of a piping system, where a liquid or a gas flows mit a certain velocity. The delay is of course somehow related to distance/velocity. And the measures could be, e.g., flow-induced vibrations or some other fluid-related measure.

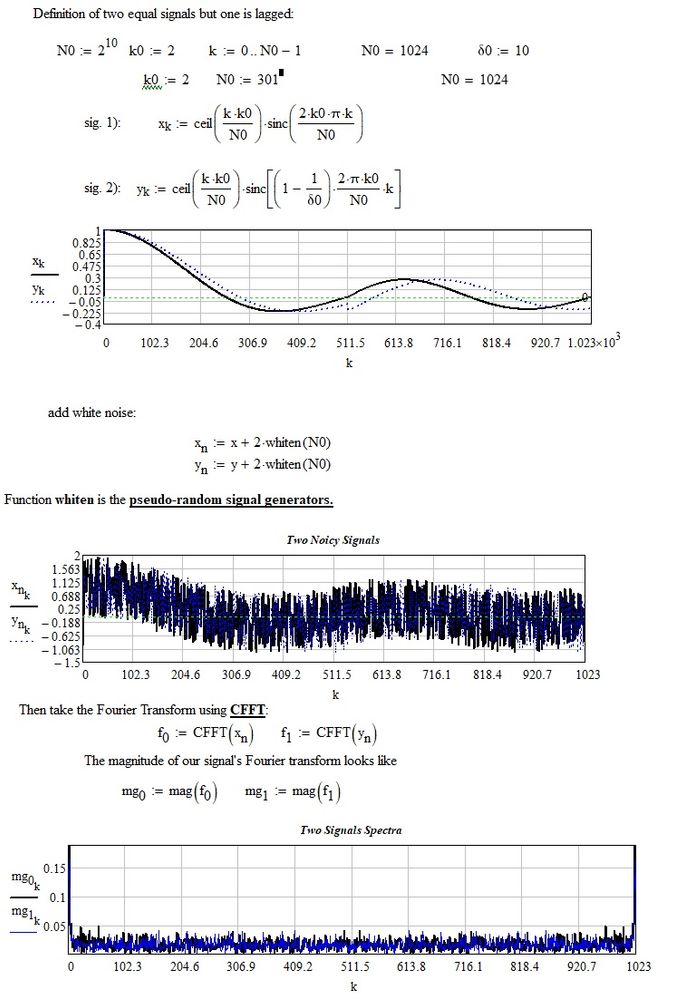
But I have a small question about your example.  Maybe I understand it completely wrong, but it seems to me that your "lag" is delta0, isn't it? the equations defining the signal seem to change the period, not the delay... or else you should put something like (k-k_delay) in the argument of sinc.  Please correct me if I'm wrong.

I will post here my original example, also based on completely invented random numbers. Part of it is in german but I hope it's nevertheless clear enough.

Thanks a lot again

Regards

Claudio

[-MFra-]

good evening,

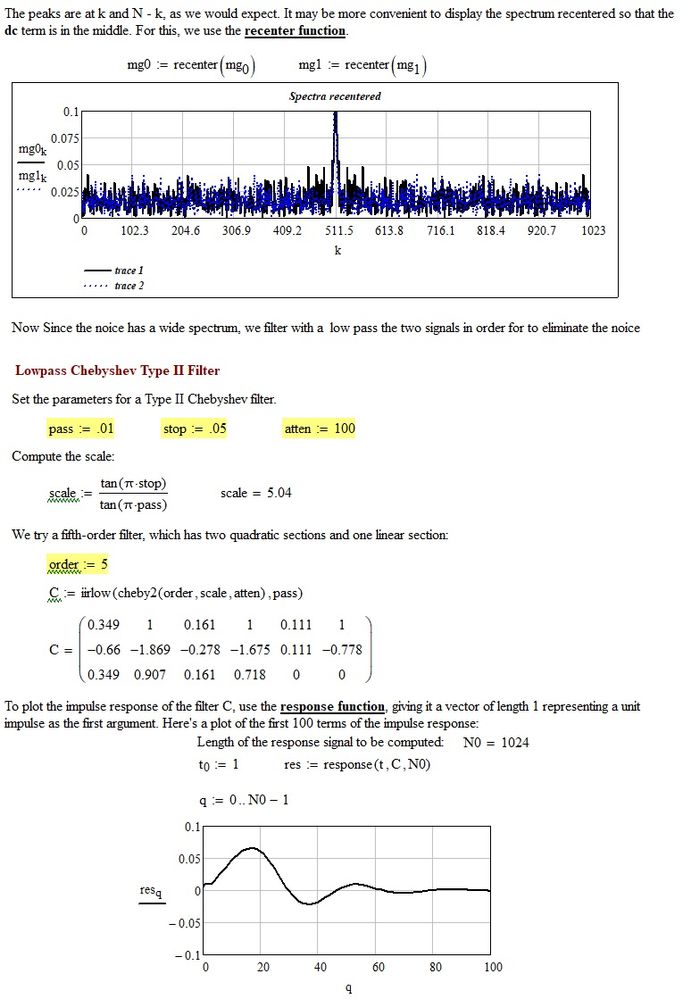
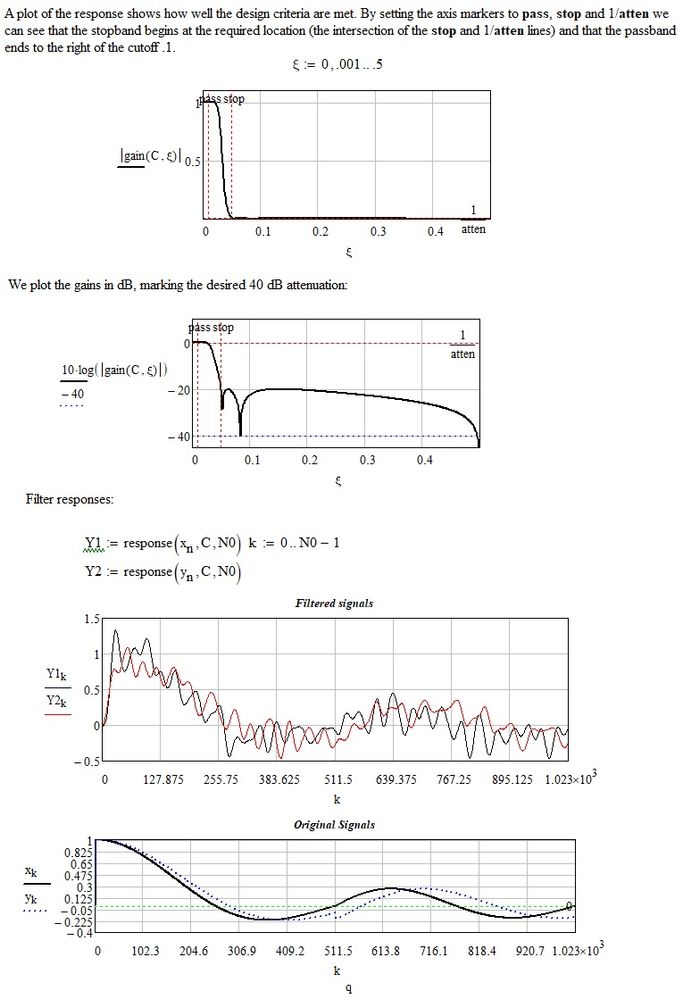
(sorry, I don't deny that I wrote my previous worksheet in a somewhat hasty way). However now I have modified the file with your data, and the result is in the attached file. I hope it goes well.

[ClaudioPedrazzi]

hi again and thanks a lot for your time and patience!

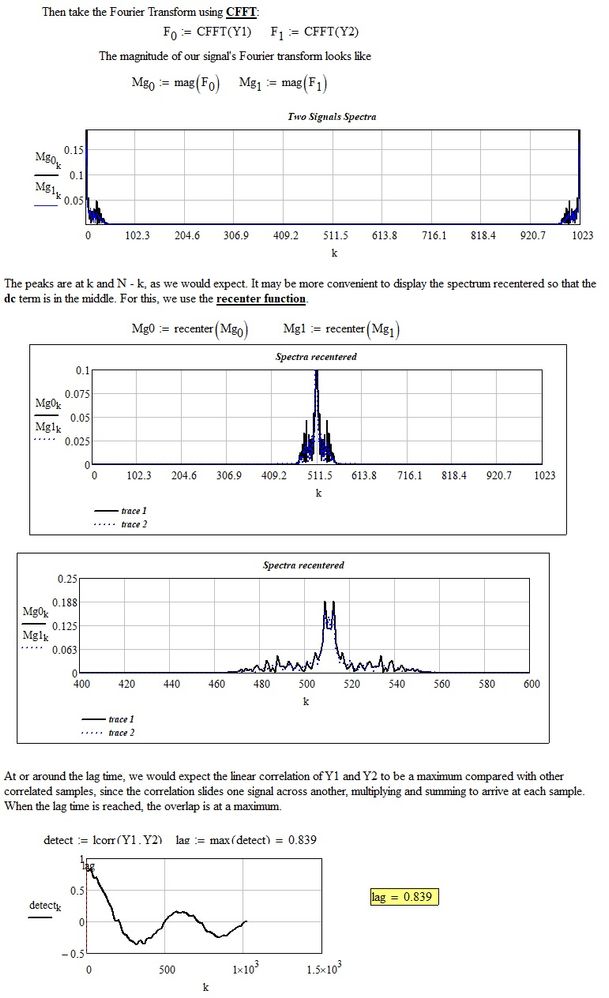
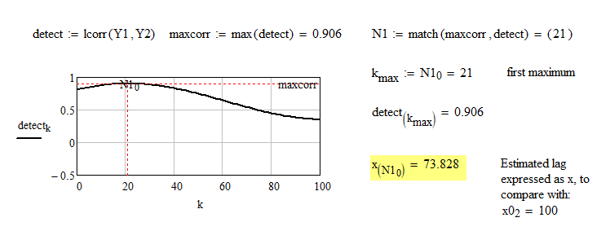
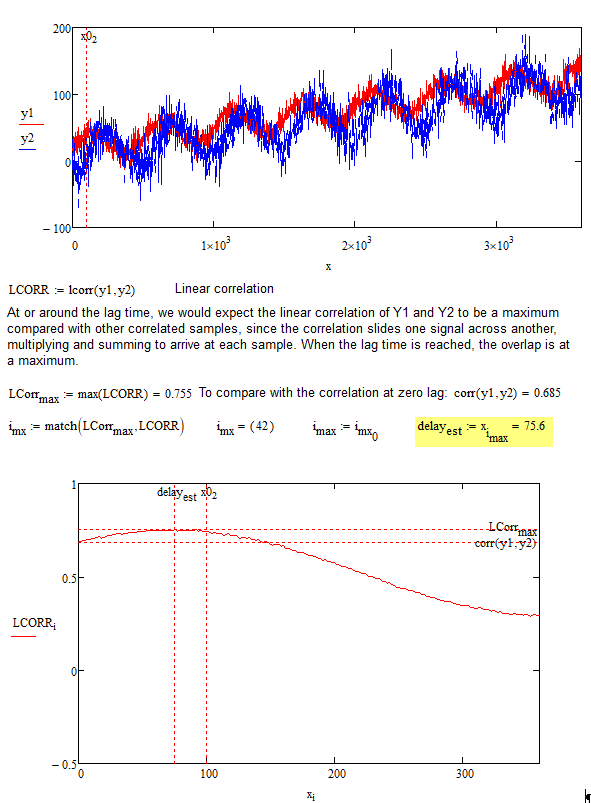
Yes, it works! only a small side remark, that IMHO the estimated lag is not the maximum of the correlation, but the x-value corresponding to the index where the correlation reaches its maximum. Something like this:

If and when you find time to answer: why is the whole processing with FFT and filtering necessary?

After all I tested a solution using directly lcorr on the original noisy functions and it is almost so good...

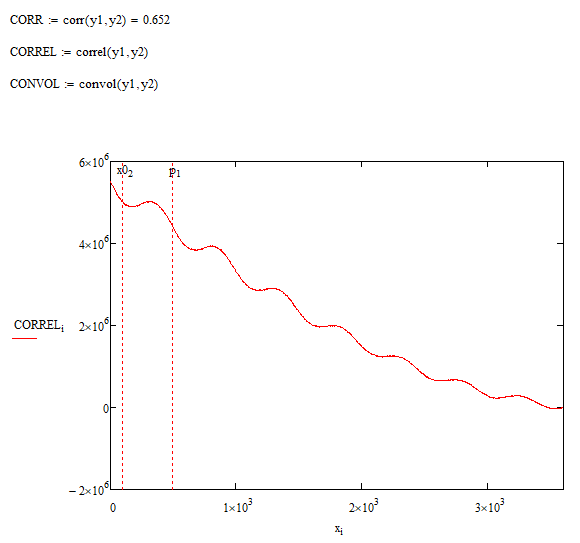
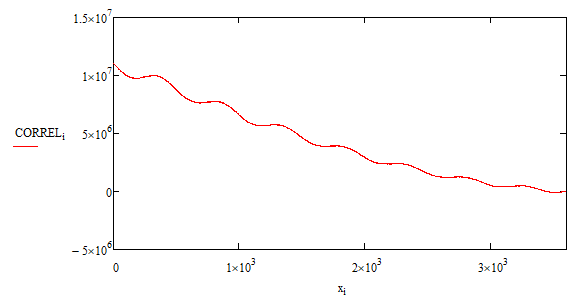
Also, something that I do not understand, due to my poor knowledge of signal analysis. What is the difference between the MathCAD standard function "correl(vx,vy)" and the Signal Processing "lcorr(x,y)" that you correctly use? I tried, but correl does not seem to provide the same answer, it is constantly decreasing, it has no absolute maximum except in x=0:

Thanks a lot, I appreciate your help really, I'm trying to give back something to the community too, whenever I can...

Regards

Claudio

[-MFra-]

Hi,

sorry, I mistakenly put lag on the graph ordinate. I cannot dwell on the answer since I am busy with other topics. Anyway, in practice, to extract a deterministic (sinusoidal) signal from a noisy channel, it is injected into a low-pass filter (to eliminate most of the noise). You can then, with a threshold system, determine the zero passages of the same signal. If there are two signals and you want the delay between the two, you can use the same procedure described above. The delay, therefore, can be determined in this way: the passage through zero of the first signal starts a timer on ns scale for example, which will be stopped by the passage through zero of the second counter. The timer's display will show the delay between the two signals. The correlation, autocorrelation functions and so on,  are defined for random signals and in general for random processes whose distribution functions and density functions are known.