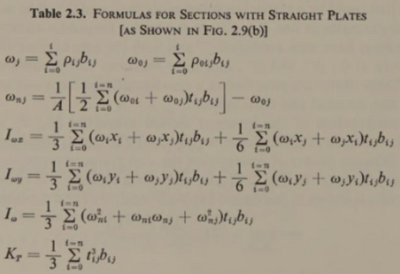Community Tip - You can change your system assigned username to something more personal in your community settings. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
FEM for section properties of a beam cross section
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
FEM for section properties of a beam cross section
When I calculate section properties for a beam, I usually run AutoCAD's MASSPROP command on the section and then do any additional analysis in MathCAD. I'm often doing composite beams, beams with custom shapes, etc. so I can't rely on magic formulas for specific shapes. There are a few properties that I haven't been able to calculate as easily, such as the torsional constant, warping constant, plastic section modulus about plastic section centroid, and monosymmetry constant. These are found using finite element analysis. I have a python API written by Robbie van Leeuwen called SECTIONPROPERTIES, and it's great but my colleagues don't know how to use Python. So with that context, my question is "How can I use MathCAD Prime to cut a section into discrete elements and run a finite element analysis or solve differential equations o?
Here's the DE for the monosymmetry constant:
Here's the St. Venant torsion constant:
The warping constant, from Galambos, 1968:
- Labels:
-
Calculus_Derivatives
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Calculate Thin Wall Section Properties "The Structural Engineer" vol 63B no 5 (1985)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you! This helps with Cw and thin-walled shapes.
However, it is not FEM. I am still looking for a solution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
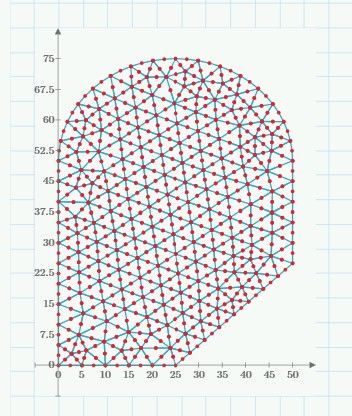
Triangulation of shapes has been discussed on this forum. Search for "triangulation".
The upshot is no one has written a triangulation routine and shared with the forum.
It would be easier to teach the engineers python than write a mathcad Prime triangulation.
Good resource "Robbie van Leeuwen called SECTIONPROPERTIES"
Thank you
Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Kevin,
Part of your question was "How can I use MathCAD Prime to cut a section into discrete elements?"
SECTIONPROPERTIES by Robbie van Leeuwen uses six nodes per triangle.
I have also wanted to be able to do this. After looking around I have found this.
Using a program called Gmsh https://gmsh.info/ this is possible in PTC Prime by text processing for input and of output.
Gmsh is open source.
The second part of your question
and run a finite element analysis or solve differential equations
SECTIONPROPERTIES by Robbie van Leeuwen uses an Iterative Conjugate Gradient Scheme on Sparse Matrix for solution of the FEM.
This is beyond the capacity of Mathcad as it has no sparse matrix definition and algebra capabilities.
Cheers
Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Kevin,
Step 2 taken the solution further by obtaining the section geometric properties from the six-node triangle triangulation.
I have not derived other geometric properties as this is trivial to do from the basic ones.
.If you want this extended to the calculation of J, and Cw I need some feedback that it is needed.
Cheers
Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Terry,
I saw this and thought I would compare your results with those from my AREA Mcad 14 work sheet.
This entails some approximation as only straight line segments are used, (and also your XX axis is my YY, and vice versa). I found good agreement for the area, and the centroid distances but I do not agree with your results for Ixx and Iyy. I also ran this example through a BASIC version of the process which does allow curvilinear segments; this gave A=3169, Ixx=1.202E6 and Iyy=5.68E5 (my yy and xx!). My approximation of the curve with the straight lines evidently produces errors of about 3% only, well within engineering tolerances.
So, whilst I'm very impressed with the triangular meshing, I think the inertia results are wrong.
I first saw the integrating between the line and the axis process demonstrated at the Institution of Civil Engineers HQ at a symposium in about 1965, it was carried out on an HP 9800 programmable calculator, I was amazed to see thta the properties of are could be calculated just by tracing round the perimeter clockwise, and also by the fact that holes can be accomodated by going round anti-clockwise!
regards, Bill
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Bill,
Was doing the FEM method as an example for the original poster to show it could be done. Dimensions are mm. FEM is an approximation method not an analytic solution and should be treated as such.
Results are as a comparison. FEM values also are close to values from commercial software Rhinoceros as illustrated in last post.
FEM also can approximate torsion and warping constants for the section. Working on this but getting problems but close.
Calcs Clockwise FEM Basic
A 3169 vs 3157 vs 3169
x_bar 23.36 vs 23.35
y_bar 37.25 vs 37.70
Ixx_c 1.162e6 vs 1.193e6 vs 1.202e6
Iyy_c 553e3 vs 563e3 vs 568e3
Ixy_c 147e3 vs 141e3
I11_c 1.195e6 vs 1.223e6
I22_C 519e3 vs 533e3
Iox 5.491e6 vs 5.679e6
Ioy 2.256e6 vs 2.284e6
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Bill,
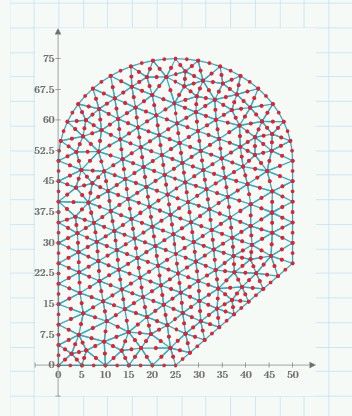
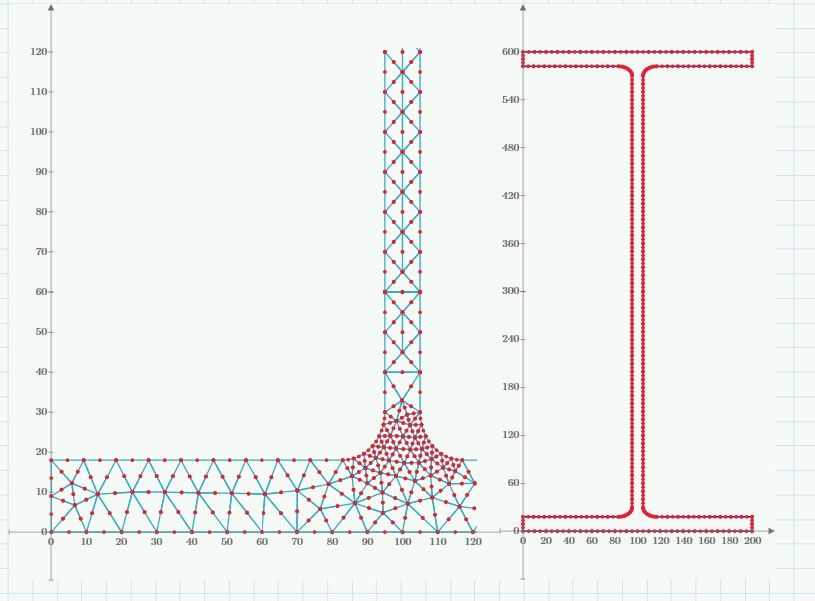
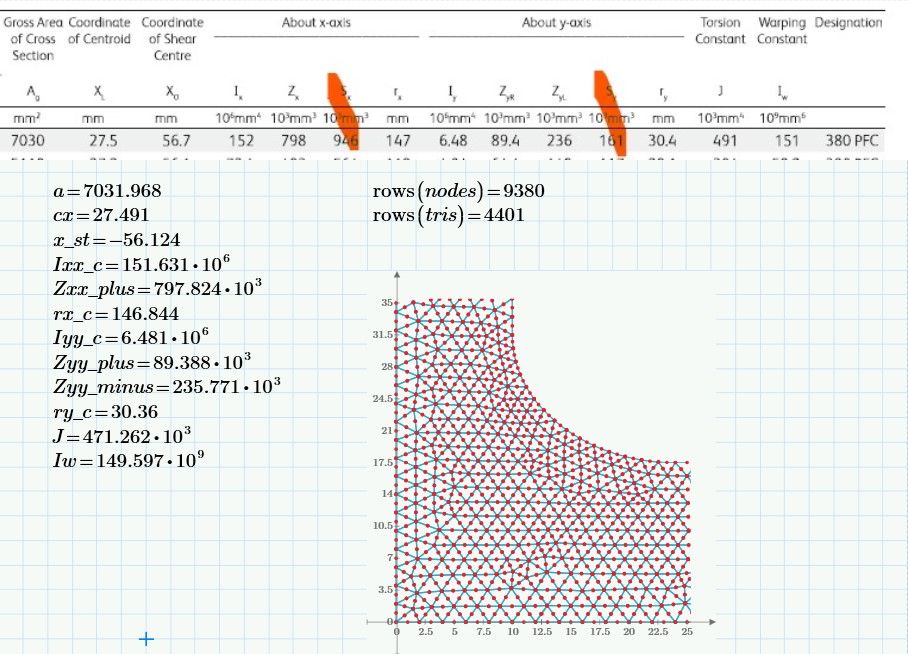
FEM gets closer to analytical value the finer the mesh is used. This is with use of 9380 nodes and 4401 six node triangles in the approximation of a standard section 380 Parallel Flange Channel for which published data is available. Takes 15 GB of ram to hold the global dense form stiffness matrix so many laptops and PC's may not handle the memory requirements. Note how approximate the values are 🙂
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you, everyone! I really appreciate the help with this. It will take me a bit of time to go through the sheets you shared, and right now I'm very busy with other tasks at work. Feel free to continue the conversation, though. I am reading everything.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Kevin
A word about accuracy and Prime memory requirements.
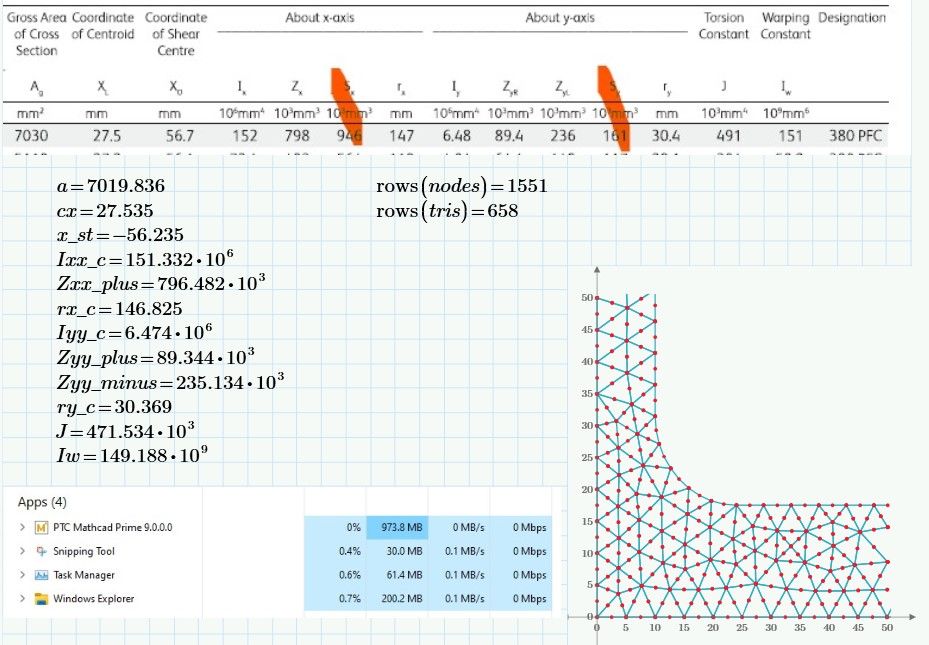
With a drastic reduction in mesh size only a small loss of accuracy is achievable. It is a trade-off. With 1551 nodes (not 9380) you get a size that fits on a 4 or 8 GB machine.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Kevin,
Am now happy with my sheet as far as it goes. Geometric properties just uses numerical integration over the section. Warping constant Iw uses a finite element technique to derive the quantity.
So have demonstrated PTC Prime with text file manipulation and Gmsh program can do triangulations of six node triangle elements.
Also demonstrated finite element analysis of section to derive warping constant.
Cheers
Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Looking at your list I can see that I read your Iox and Ioy results as being Ixx and Iyy, that explains the confusion. I thought there must be an explanation.
Regards Bill