- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Fermi integral (01)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fermi integral (01)
Hello All,
I am trying to calculate the Fermi integral of the order of 1/2 and its derivative. In the attached worksheet, the integral cannot be evaluated for x>0. I used an approximated model as is given in the following article but the result is not similar to what the article obtained.
Koroleva, Olga & V Mazhukin, A & Mazhukin, Vladimir & Breslavskiy, Pavel. (2016). APPROXIMATION OF FERMI-DIRAC INTEGRALS OF DIFFERENT ORDERS USED TO DETERMINE THE THERMAL PROPERTIES OF METALS AND SEMICONDUCTORS. MATHEMATICA MONTISNIGRI. 36. 37-53.
Could you please help me with this problem.
Thank you very much in advance.
Payman
Solved! Go to Solution.
- Labels:
-
Calculus_Derivatives
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
To get single values you may consider using symbolic evaluation with "float"
For numeric approximation (for plotting) you may also use the same integral with a rather high upper value (not sure in which range this would be an acceptable approximation)
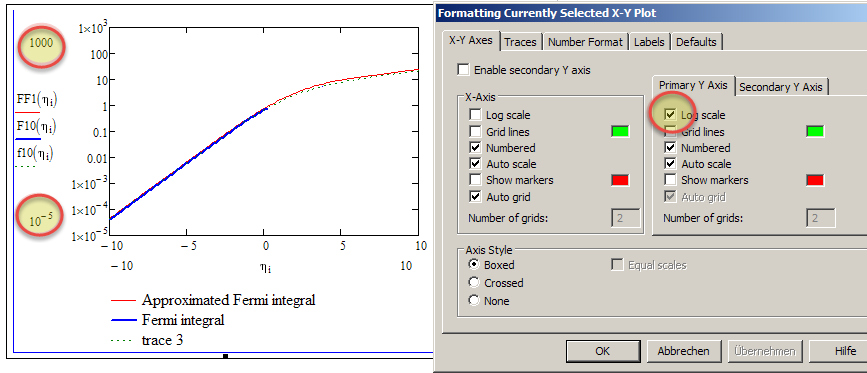
And to make your plot to math the one you try to duplicate you will have to
- not use the secondary y-axis (otherwise you will have different y scales)
- set the plot-limits manually
- notice, that the plot in the article uses a logarithmic y-scale
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
To get single values you may consider using symbolic evaluation with "float"
For numeric approximation (for plotting) you may also use the same integral with a rather high upper value (not sure in which range this would be an acceptable approximation)
And to make your plot to math the one you try to duplicate you will have to
- not use the secondary y-axis (otherwise you will have different y scales)
- set the plot-limits manually
- notice, that the plot in the article uses a logarithmic y-scale
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This is the second time I noticed it - I am not offered the option to edit my post in the 3 dots menu. Anybody else having the same problem?
Just wanted to add, that you don't need to define eta as a vector and create the vectors for FF, etc.. A simple range is all thats neeed and if you are happy with the default range from -10 to 10 of the quickplot feature, you may also omit the range defintion altogether.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you very much Werner !
I don't know why, but my worksheet is still unable to perform the integration as you showed in your post. Could you please take a look?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have no idea whats going on. You file failed for me, too. But when I retyped the definition for F10 the very same way you did, it worked - no clue why. I attach the file - hope it works at your end, too.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I really wonder what the reason for the error is if we feed the function defined with upper limit infinity with values higher than the one shown in the picture below
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator