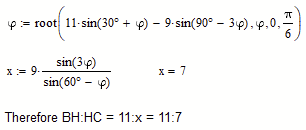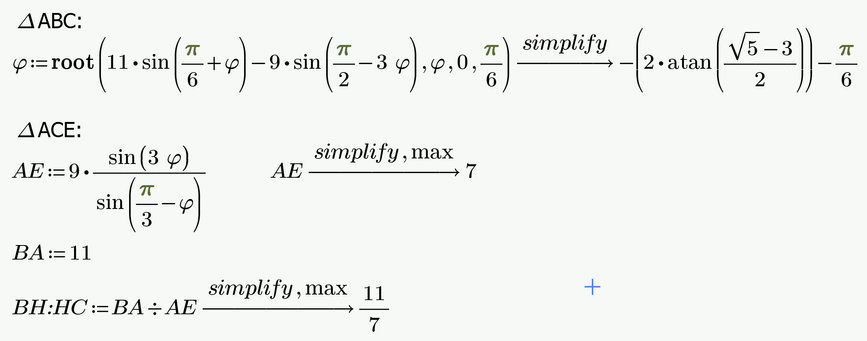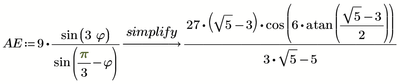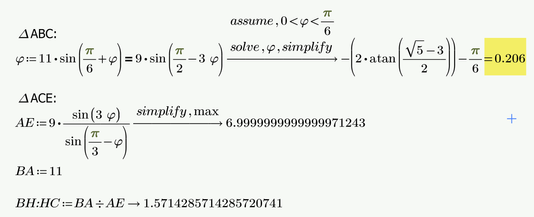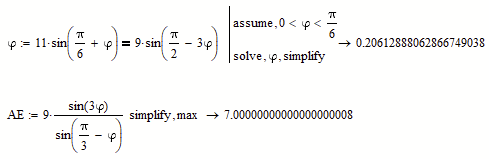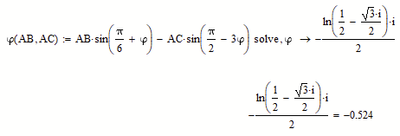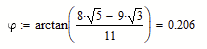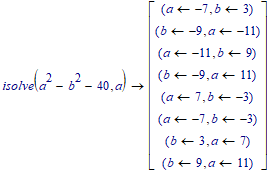Community Tip - Need to share some code when posting a question or reply? Make sure to use the "Insert code sample" menu option. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
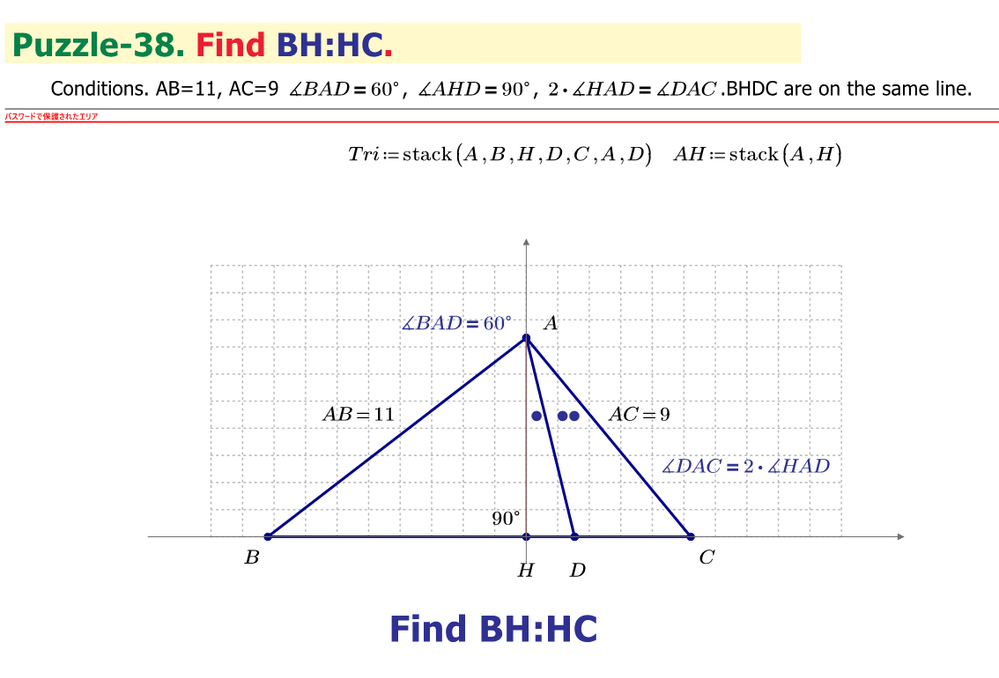
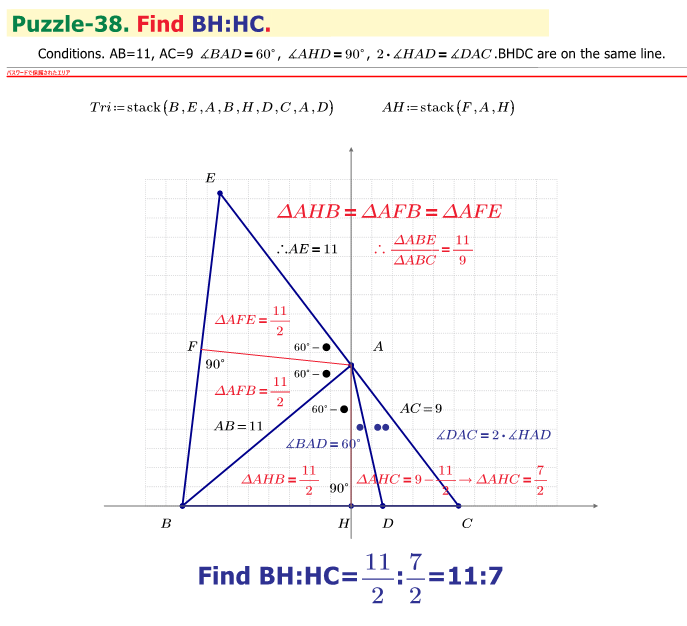
Find BH:HC
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Labels:
-
Puzzles Games
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Guess there is an easier, elementary way to come up with 11:7, right?
Haven't found it yet, though.
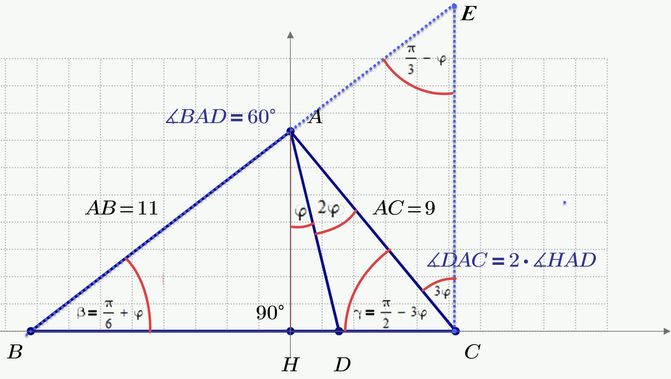
EDIT: Here a little more explanations using a drawing and calculation done in Prime:
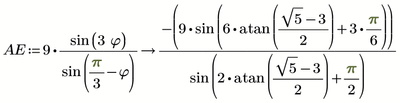
We now use the law of sine in triangles twice to calculate the length AE:
Prime 9 sheet attached
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Guess there is an easier, elementary way to come up with 11:7, right?
Haven't found it yet, though.
EDIT: Here a little more explanations using a drawing and calculation done in Prime:
We now use the law of sine in triangles twice to calculate the length AE:
Prime 9 sheet attached
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Elegant solution! In particular the trick to get the ratio you are looking for using the ratio in similar triangles. The only thing that is unclear to me about how MC works is: What is inserted from the equation phi:= ... into the equation AE:= ..? Is it the number phi or is it a logical structure that is then processed by MC according to implemented rules? So in MC does this step involve calculating numbers or transforming them algebraically according to rules?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@AlfredFlaßhaar wrote:
Elegant solution! In particular the trick to get the ratio you are looking for using the ratio in similar triangles. The only thing that is unclear to me about how MC works is: What is inserted from the equation phi:= ... into the equation AE:= ..? Is it the number phi or is it a logical structure that is then processed by MC according to implemented rules? So in MC does this step involve calculating numbers or transforming them algebraically according to rules?
That depends on how you evaluate AE later. If you evaluate it numerically (normal equal sign), only the stored numeric (approximated) value is used for phi. But if you evaluate it symbolically (right arrow) as I did, the symbolics traces back the calculations up to the definition and so it uses the exact algebraic expression which you see at the end of the assignment line phi:=...
So, yes, Mathcads symbolic uses the exact algebraic expression and simplifies it according to the rules. But it has a hard time doing so.
Without "simplify" we get
Using "simplify" still does not do the job
It was necessary to use "simplify, max" to get the desired result 7, as you can see in the posted picture.
If I would have followed the definition line for phi with an immediate numeric inline evaluation, though, then the symbolic would use this approximated value (about 15-16 decimals, the usual IEEE limit) as the definition of phi and would yield just an inaccurate numeric result for AE (default precision is about 20 decimals, could be set higher using the "float" modifier) and also for the ratio:
This unfortunately will also be the case when you try to duplicate the calculation with your MC14, as the symbolics in that version (while usually superior to the one on Prime) is not able to come up with an exact algebraic solution for phi but rather yields just a numeric one.
It could be that if we help Mathcad by simplifying the equation (maybe by applying the rule for the sine of a sum of angles) that good old Mathcad would be also able to provide a symbolic solution - I had not tried to do so, though.
I guess that the symbolic engine in Mathcad 11 (an older version of Maple) as still used by @LucMeekes will do better ...
Actually I wonder how I would solve the equation for phi without the help of Mathcad or Prime. Applying the rule for the sine of a sum of angles yields a cubic equation for sin(phi) and Cardano isn't really something I'd like to do without the assistance of Mathcad or similar programs.
That's the reason I suppose that the tasks solution may have a simpler and more basic approach - I just don't see it ...
Maybe @ttokoro will reveal a simpler, more basic solution when he finally closes this thread.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mathcad 11 will do:
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
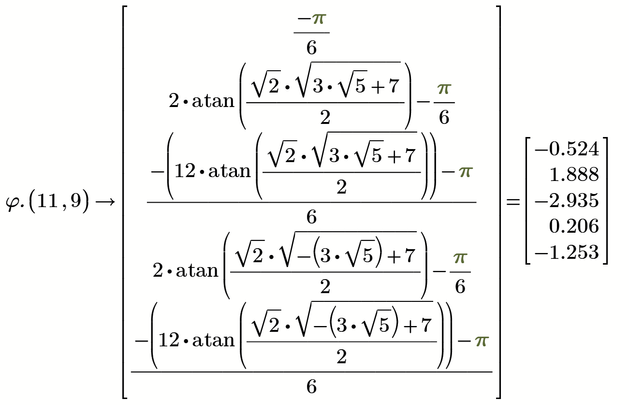
I guessed that old Maple in MC11 would be able to deliver.
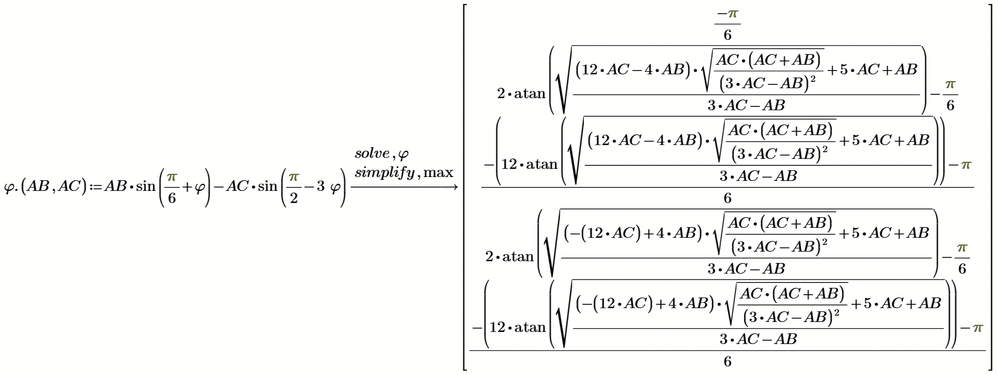
MC15 gives just the solution -pi/6 written in a strange way 😞
using "fully" makes the expression fail as of an undefined variable (!?)
Prime 9 seems to do better
The solutions have a pi-periodicity, so it would be logical to just show three solutions (within an interval of length pi) or, as Maple does, six solutions within an interval of length 2 pi.
Showing five solutions is a bit unlogical.
Trying to use "fully" resulted in en 'endless' calculation which I had to interrupt.
The performance of MuPad in MC15 is indeed disappointing, though.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The 3rd degree polynomial is quite difficult to find. But it can be factored into handy polynomials. It cost me an hour of MC and is certainly not an elegant solution. Nevertheless, there is an interesting task that somehow reminds me of temple geometry.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Your worksheet is missing 😉
Nevertheless, there is an interesting task that somehow reminds me of temple geometry.
Who knows - maybe its a task out of a collection of Sangaku problems ...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, thats neat!
Mathcads symbolics is used for factorization only.
I still wonder how to solve it without symbolic math power. I wouldn't have been able to do the factorization by hand.
In any case the solutions
or
are much nicer than what Prime came up with!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Please submit the file as readable in MC14.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@AlfredFlaßhaar wrote:
Please submit the file as readable in MC14.
I guess @ttokoro can't do so as PTC provides no way (other than retyping) to convert a Prime sheet into real Mathcad format.
But the tasks seems to be clear from the description and the picture anyway, so you won't need the sheet and can start a solution with the version of Mathcad you have.
EDIT: I just added a more detailed explanation of my approach in my answer above and used Prime symbolics to do the job.
Often Primes new symbolics is mediocre compared to Mathcad's (MuPad in MC14 & 15) but in this case it came up with a symbolic solution for the angle phi whereas the symbolic in Mathcad only gave a numeric result.
Would be interested if someone can come up with a simpler, more basic solution without using Primes solve facilities (symbolic solver, "root" function, solve block with "find").
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I don't have a simpler solution, just a numerical force solution made on the fly (time constraints). The common height of the two right triangles provides the beginning. For tasks with different solution paths, I am mainly interested in the solution paths/thinking of the solvers. That's why I asked for a file for MC4. Let's see if something classically geometric is possible without MC and trigonometry.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here's an algebraic solution:
Lou
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
By the way:
Considered as a Diophantine equation, your equation #1 would have the solutions (a,b)=(11,9) and (7,3).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And a few more. I guess this is the total set:
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, these solutions are all well known. It's not without reason that I didn't use symmetrical and negative solutions 😉 . Can Mc14 solve Diophantine equations? I used Dario Alpern's app.
Alfred
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
"Can Mc14 solve Diophantine equations?"
Not as far as I know.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
... and now the question of all questions ;-):
Can the line BC be constructed using a compass and ruler without knowing its already calculated length?