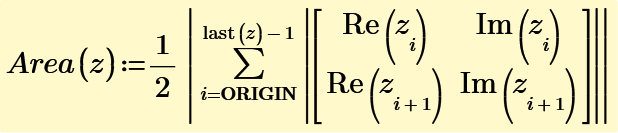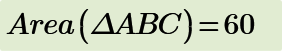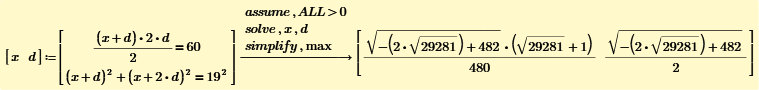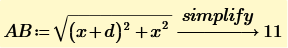Community Tip - Did you get called away in the middle of writing a post? Don't worry you can find your unfinished post later in the Drafts section of your profile page. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
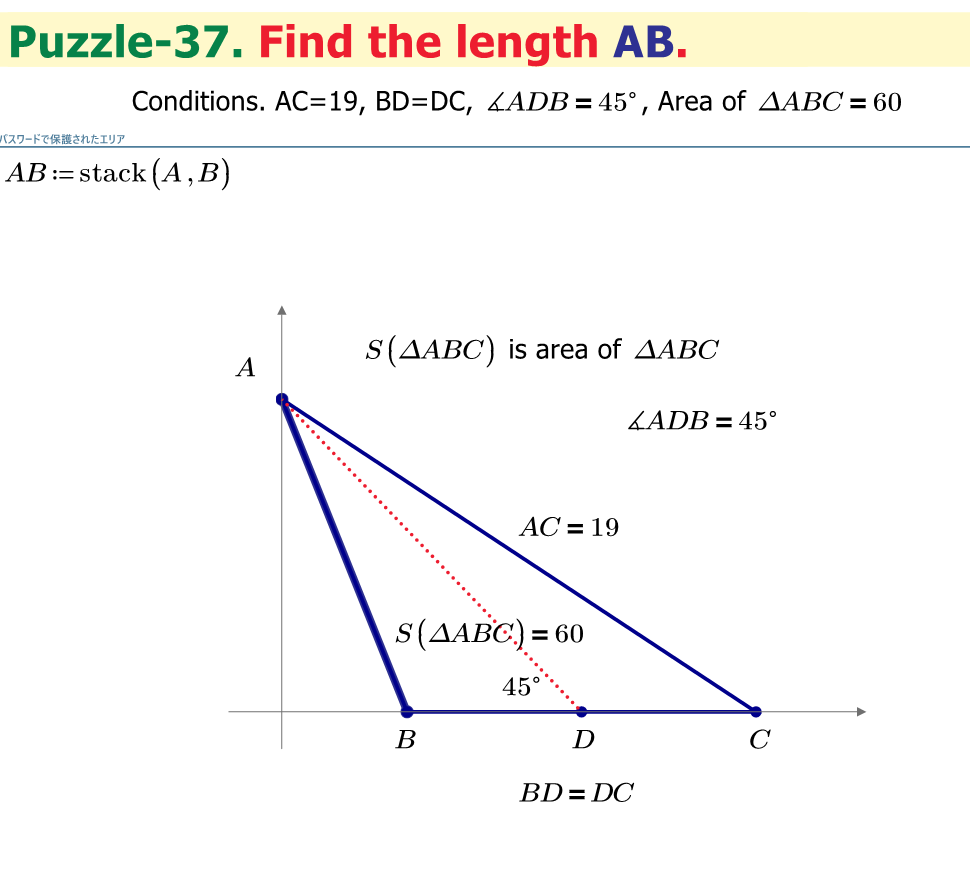
Find the length AB.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Find the length AB.
Elementary schoole children can solve this puzzle. If you need you can use Mathcad Prime.
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There are two intermediate solutions. In the end AB=11 in any case 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
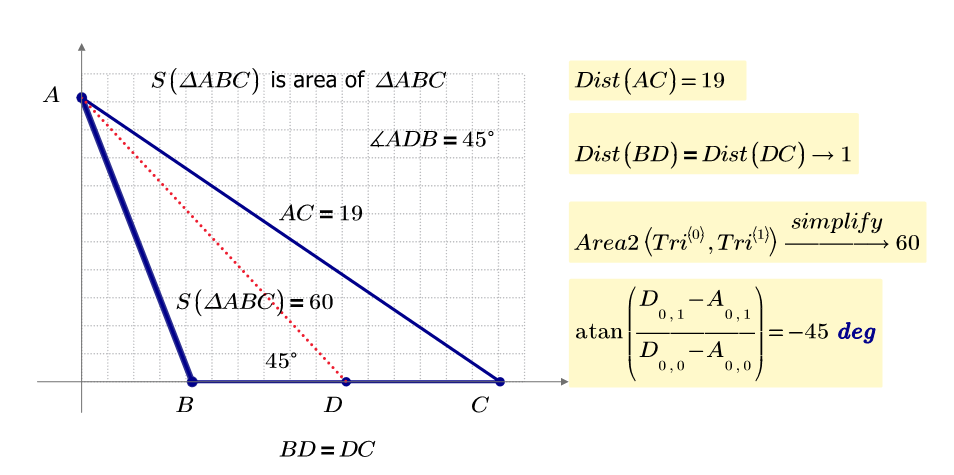
If we use Mathcad it is easy to find the answer. But without sqrt or functions, this puzzle becomes very hard.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This task is not particularly difficult. Students should be able to solve it using the cosine law for side length and the sine formula for the area of a triangle. What is much more interesting about this problem is that solution "11" is possible in two different geometric situations.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
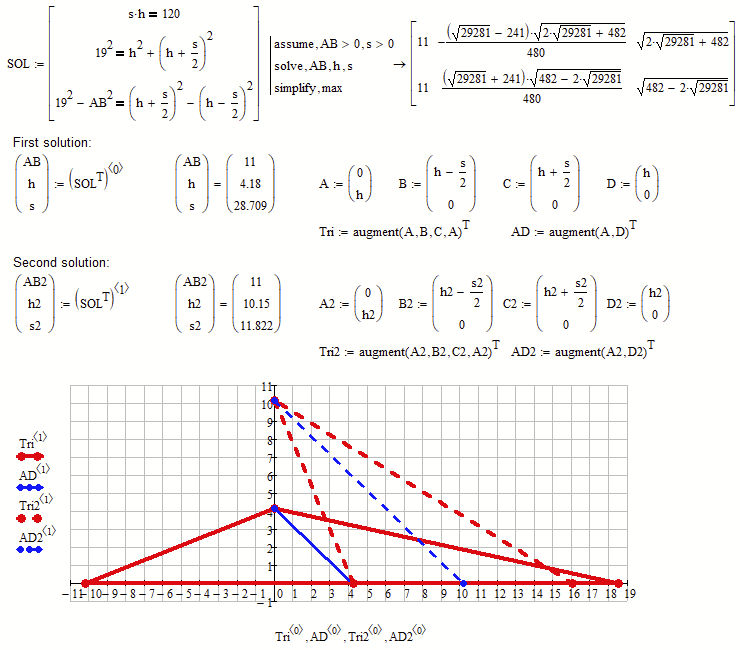
The two solutions are AD=14.354..., BC=11.822... and AD=5.911..., BC=28.709...
They are approximations for unpleasant radicals.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
BTW.
Numerical solutions attached. How do you solve the system symbolically? Need help.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
My answer is.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Additional task: 😉
Given pieces and requirements as usual.
But:
Instead of the given area F=60, the distance AC must now be calculated so that the area of the triangle ABC is maximum. How big is the interior angle at C?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Correction:
With the unusual names of the triangle vertices as shown in the sketch in the original problem, the distance AB is logically sought. I accidentally had the usual point designation in my head, where A and B limit the lower side of the triangle and C is the summit.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I would solve it that way:
Using Mathcads solving and plotting facilities it may look like this:
Mathcad 15 sheet attached