Finding curve

[VladimirN]

I want to approximate the experimental data by a curve as shown below on screenshot. I tried to use inverse probability density for the normal distribution, but without success. Are there any ideas in this regard (which equation can describe the data or maybe I need to create several sections/parts of the curve)?

Initial data:

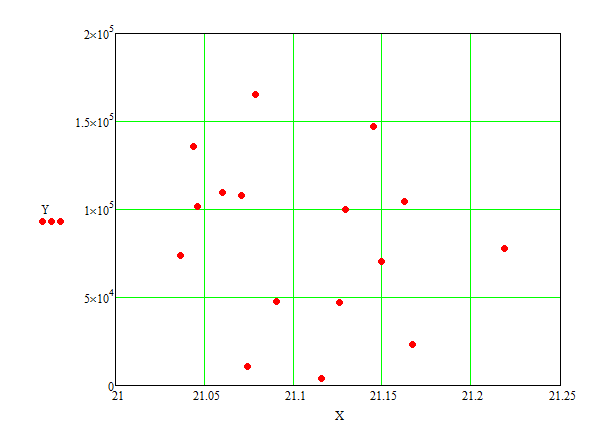
The approximating curve must have the following form:

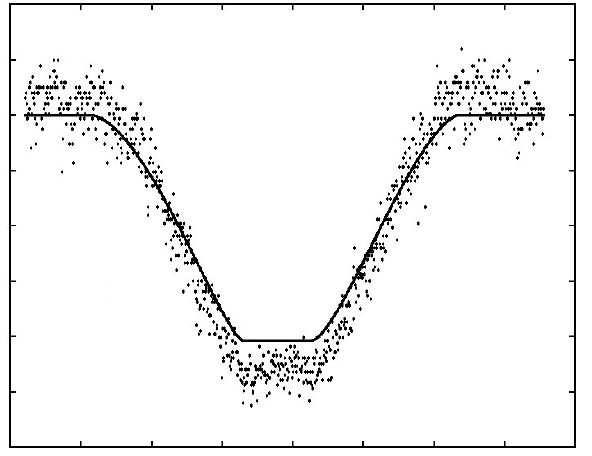
Or this form:

[RichardJ]

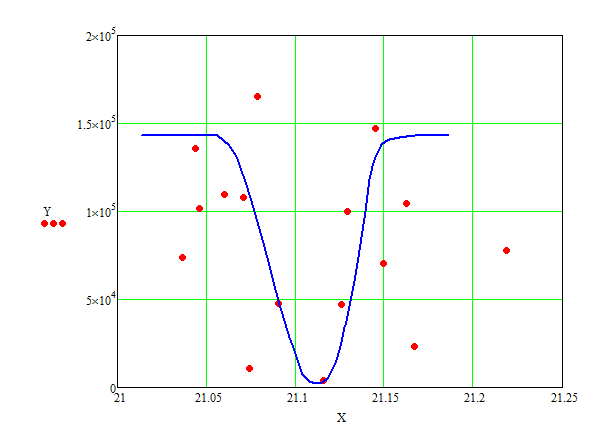
Here's one possibility. The data has so much error you are unlikely to get a curve that looks like what you want though. The fitted parameters will be pretty much meaningless too.

[ValeryOchkov]

See please Figs 12.9, 12.12 & 12.13 here

Этюд 12. Нечеткое множество или Оптимальное пожарное ведро

[VladimirN]

Richard,

Thank you. Whether and there are any ideas how to correct your model on a case of transition to a decimal logarithm?

[RichardJ · Accepted solution]

Do you mean putting the Y data on a log10 scale?

[VladimirN]

Thanks!

[VladimirN]

Richard,

Could you please explain what technique you used to set the approximating function and selection of the coefficients/constants in the equation?

[RichardJ]

I'm not sure what you mean. You started with dnorm, which has two parameters. One controls the shift along the x-axis (D1) and one controls the width (D2). It seemed clear to me that two more were needed to make the curve pass through the data: one to scale the y-axis and one to offset on the y-axis. So I added D3 and D4.

With the logarithmic y-scale I forced D2 to a positive value (using |D2|) because genfit was trying to make it negative, causing the fit to fail.

I chose the guess values by temporarily changing F(x):=f(x,D) to F(x):=f(x,guess) and adjusting the guess values until the curve roughly passed through the data. Then I changed it back.

Does that answer your question?

[VladimirN]

Ok. I see.

[Fred_Kohlhepp]

Does the term "shotgun pattern" apply?  😉

[VladimirN]

Absolutely .