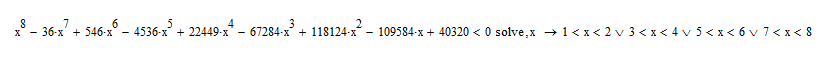Community Tip - Did you get called away in the middle of writing a post? Don't worry you can find your unfinished post later in the Drafts section of your profile page. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Finding local min ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Finding local min ?
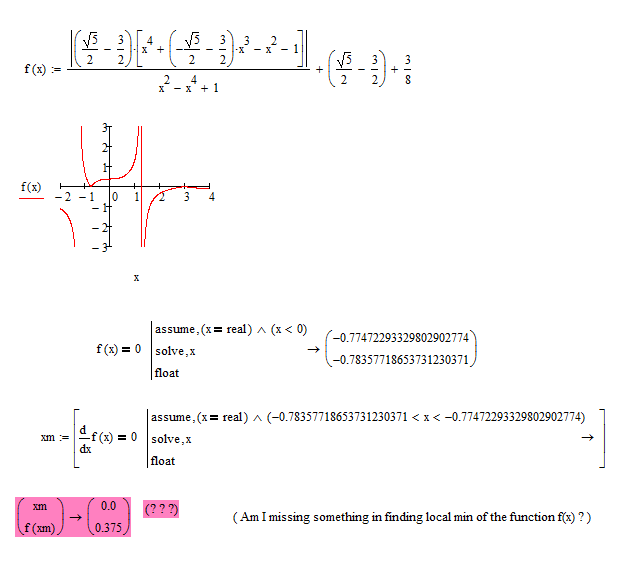
Hello Everyone.
From :
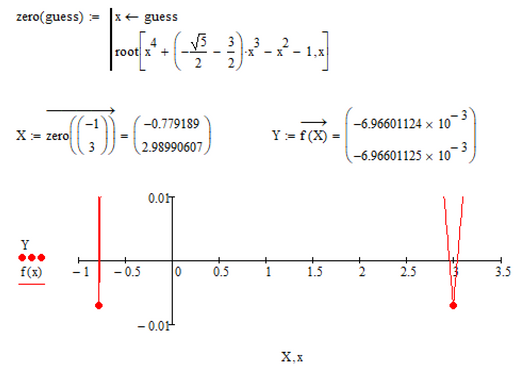
Am I missing something in finding the local min of the function f(x), the above ?
Thanks in advance.
Solved! Go to Solution.
- Labels:
-
Math Homework
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
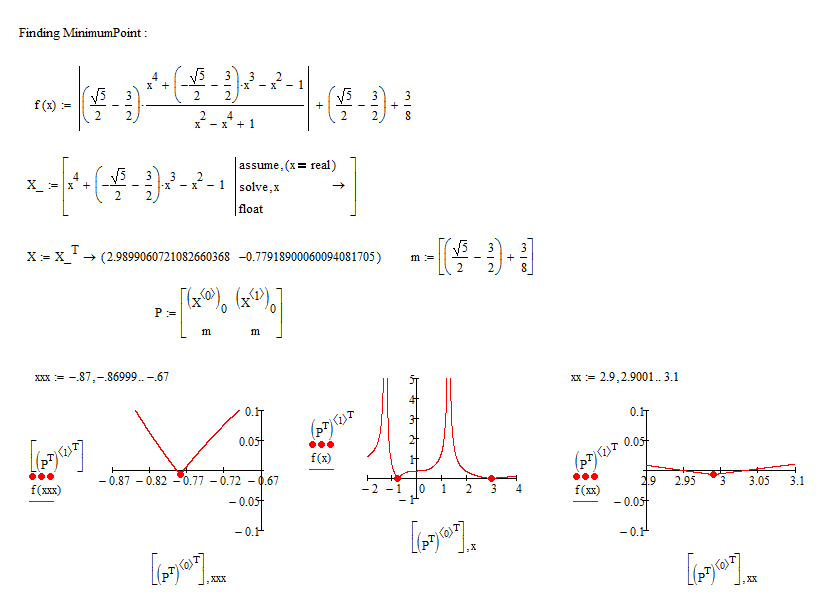
I'll spare you a picture of the symbolic solution (4 pages high, 16 pages wide), but this is what Mathcad 11 (with Maple) makes of it:
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Many thanks, Luc. ![]() I need help with graphing the point of local min of the function f(x), the above.
I need help with graphing the point of local min of the function f(x), the above.
Regards.
Loi.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Many thanks, Werner. ![]()
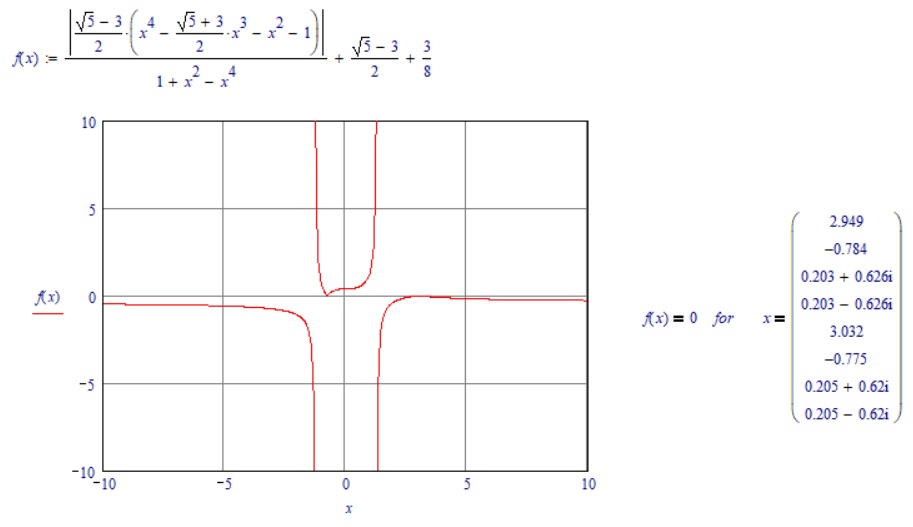
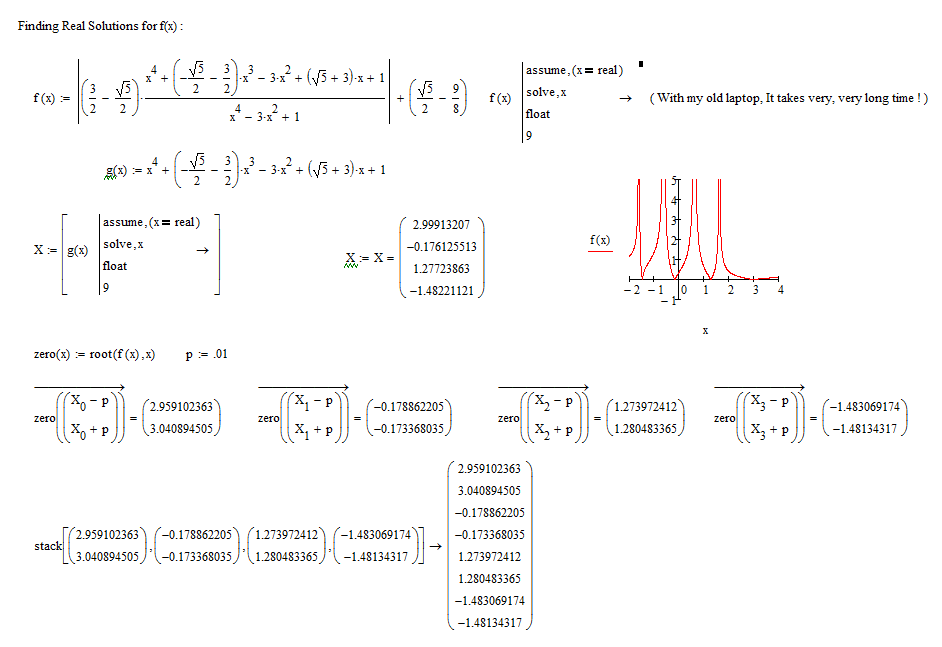
![]() The hint is very helpful to me. I guess the hint works well with the similar function :
The hint is very helpful to me. I guess the hint works well with the similar function :
Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@lvl107 wrote:
Many thanks, Werner.
The hint is very helpful to me. I guess the hint works well with the similar function :
Obviously, as your screenshot proves.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There is no need to use the symbolics (which will give you just numeric results anyway). You may consider using a solve block or the root command with appropriate guesses to get the two critical points:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Many, many thanks for another help, Werner. ![]()
![]()
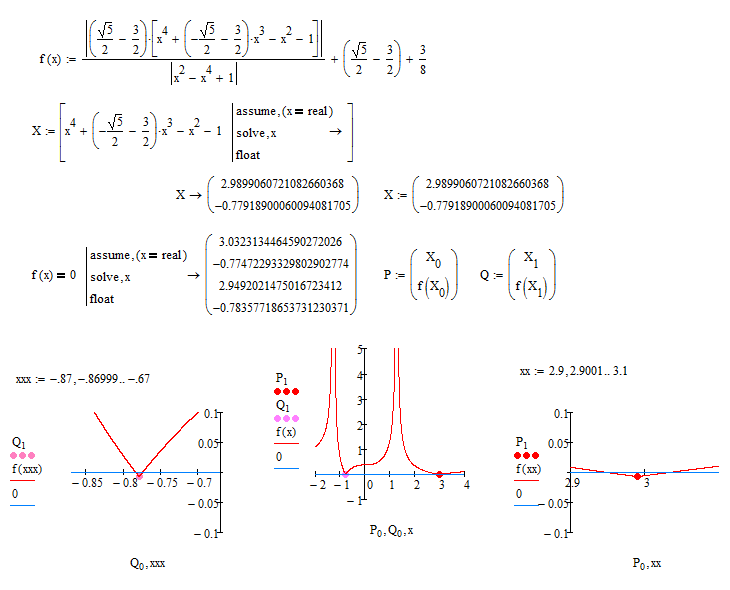
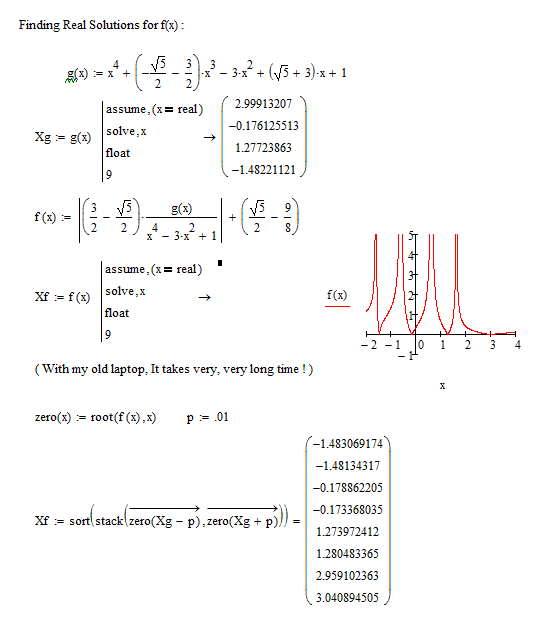
![]() And I am trying to solve another similar function :
And I am trying to solve another similar function :
Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Looks like the results of your numeric workaround are accurate enough
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
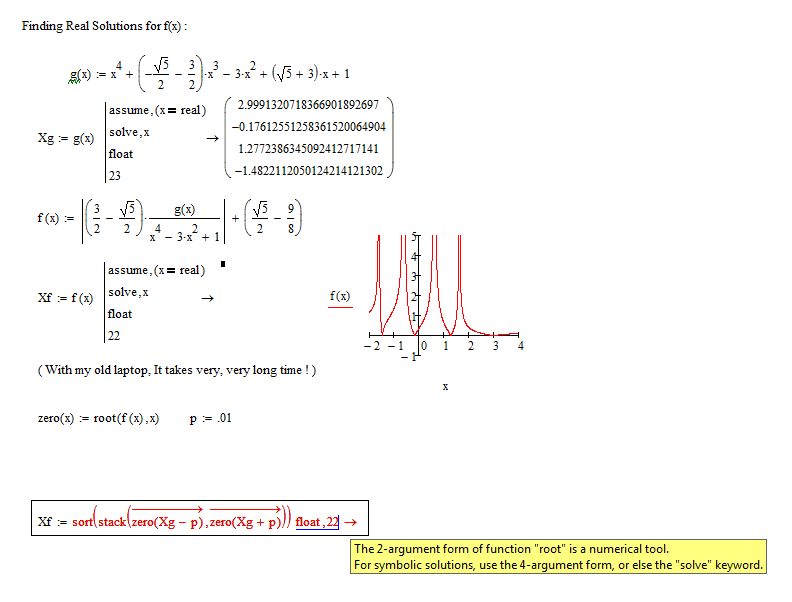
What is the 4-argument form ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@lvl107 wrote:
What is the 4-argument form ?
The error message is talking about the "root" command. It has two forms.
The first uses just a start guess value -> root (f(x), x)=
The second uses an interval and thats the 4-argument form -> root(f(x), x, x1, x2)=
In the second form root tries to find a solution which is within the interval [x1; x2].
For the second form to work its mandatory that f(x1) and f(x2) have different signs, otherwise you get an error.
You may consider looking up "root" in the help and there also is a available a quicksheet about the use of the root command.
But in your example I see no benefit in evaluating the expression symbolically - just use numeric evaluation for a quick result.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It may not be able to deal with the inequality. Will it solve for equal?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There are equations of higher order which Mathcad can reduce and solve via symbolics and there are quite more equations (or inequality) which Mathcads symbolics can't solve.
Have you tried if Wolfram Alpha can solve your original inequality?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It means what it says 😉
Mathcads symbolic simply is not capable enough to find a solution to this inequality.
EDIT: In your example which works OK Mathcad has only to deal with quadratic equations -> no problem
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Many thanks again for your time and help, Werner. ![]()
![]()
Best Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
and how to solve "by hand" ?
Best Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Maybe it would be a good idea if you tell us why you need those calculations. There may be other ways to achieve the real task you are looking for.
Concerning the intervals where the absolute value is lower than the RHS you may let Mathcad solve the equations
LHS=RHS ->
and
LHS=-RHS ->
and take the appropriate values which form your two intervals.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
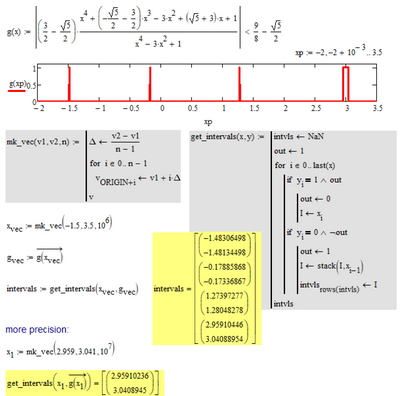
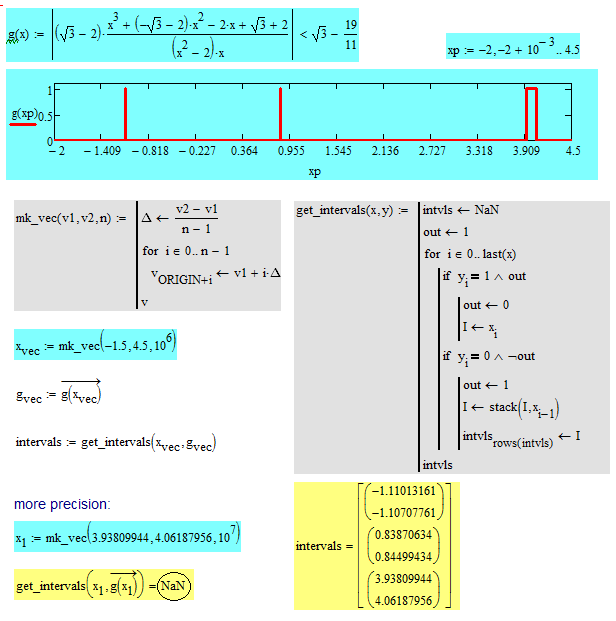
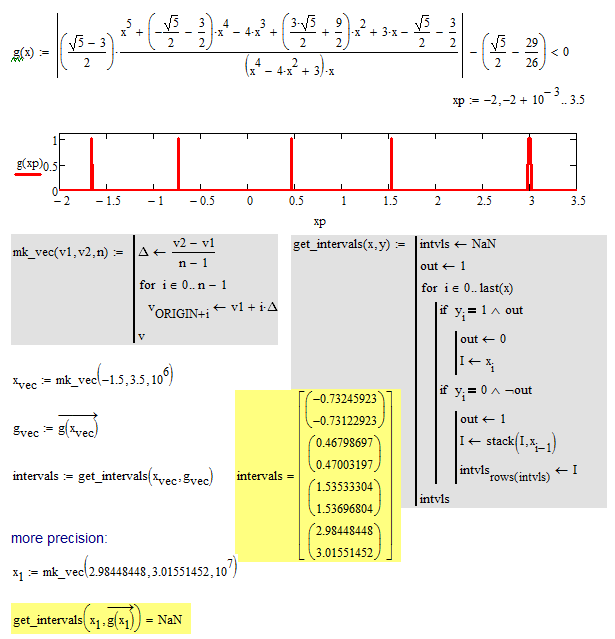
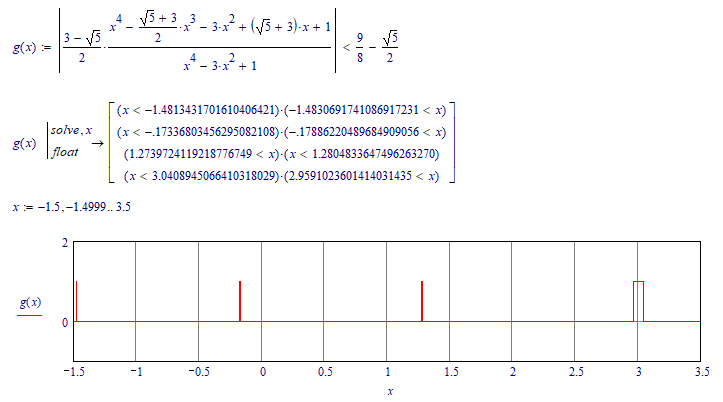
Here is a way to find the four solution intervals "by hand".
The first method uses a plot to spot the area(s) of interest and then created a large vector and picks up the appropriate values from there. You may refine the precision by narrowing down the range of interest (as shown in one example).
The second method shows a way to use symbolic calculation and was already described in my answer above.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This reply is to say thanks again, Werner. ![]()
![]() . The following, it seems there no more precision. ( I just self-check my understanding about this )
. The following, it seems there no more precision. ( I just self-check my understanding about this )
Best Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
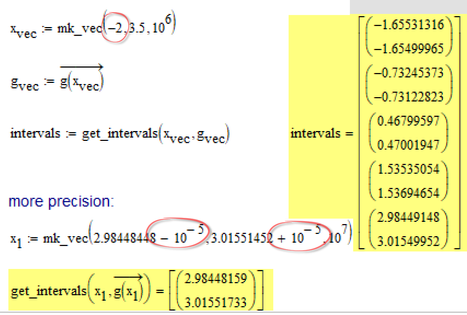
Logical plot have 5 solutions
Intervals have only 4 solutions. ( It seems missing one )
Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@lvl107 wrote:
Logical plot have 5 solutions
Intervals have only 4 solutions. ( It seems missing one )
Regards.
Use: x.vec:=mk_vec(-2, 3.5, 10^6)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
"Mathcads symbolic simply is not capable enough to find a solution to this inequality."
There's Mathcad and Mathcad:
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@LucMeekes wrote:
"Mathcads symbolic simply is not capable enough to find a solution to this inequality."
There's Mathcad and Mathcad:
Luc
There's MuPad and then there was Maple.
Nice to see (and not too surprising) that Maple in your Mathcad 11 can do the job as expected.
Unfortunately nowadays we can't buy a Mathcad version with Maple as symbolic engine nor could we license a valid older copy of Mathcad 11 for a new computer 😞