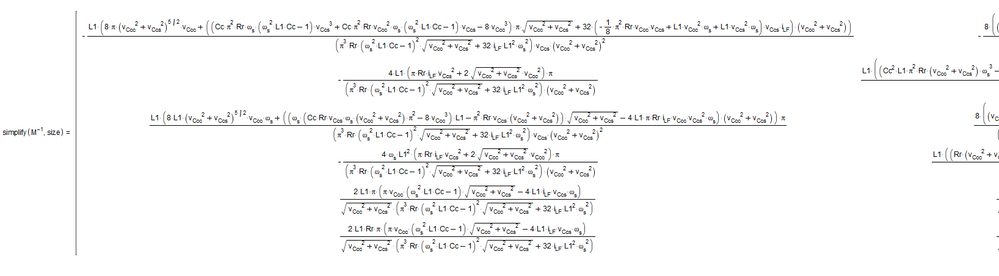Community Tip - Learn all about PTC Community Badges. Engage with PTC and see how many you can earn! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Finding the Inverse of a Matrix Symbolically
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Finding the Inverse of a Matrix Symbolically
Hello,
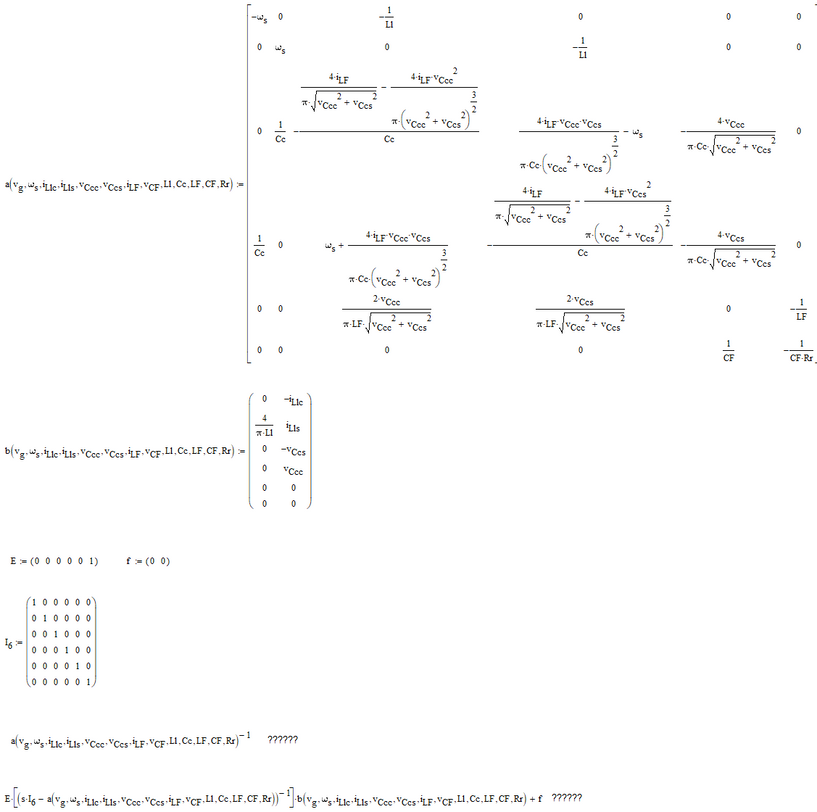
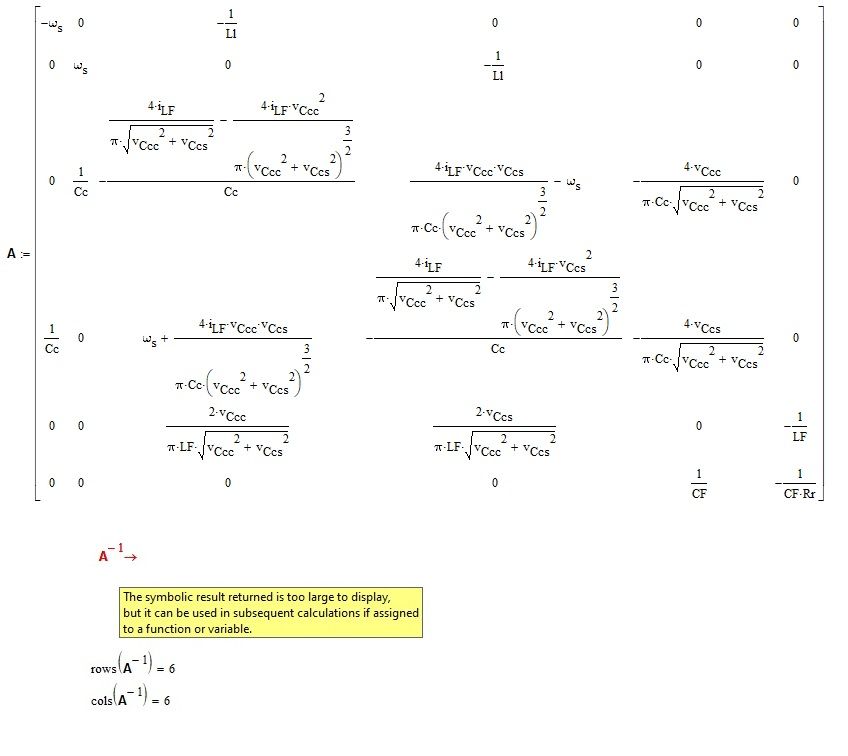
It is possible to somehow find the inverse of a() (a()^-1) and E*((s*I6-a())^-1)*b()+f symbolically?
(Mathcad 15 file)
Thanks.
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Calculating the inverse of that matrix a is a piece of cake for Mathcad 11.
The result is about 50 pages wide.
Below is a picture of the first 24.5 pages:
(unfortunately my screen isn't wide enough to show the entire expression, the zoom is limited down to 10 %, so I can't zoom out any further)
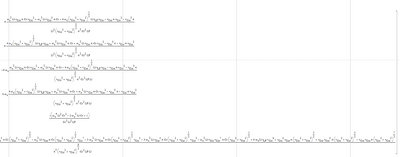
This is the first 3 pages:
This the last 3:
For your convenience, I've copied the symbolic result of the inverse to a new expression, so you can have a look at it in Mathcad 15, in detail.
Needless to say, the result of your final equation was also found, without problems.
It takes up a lot more space than the inverse of a. I've copied the symbolic result to function sol. You can have a look at that as well.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If the matrix is square, and not singular, then a symbolic inverse is possible. But I doubt if:
1. mathcad 15 can show it.
2. you will like the answer.
save the file as mathcad11 (.MCD) file and attach that. I'll see what I can do.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
"If the matrix is square, and not singular, then a symbolic inverse is possible" - Yes, I know this, that is, if the matrix is square and not singular then the inverse matrix of that matrix exists and can be calculated (because the determinant of that matrix is different from 0):))
1. "Mathcad 15 can show it." - this is the point, Mathcad 15 cannot show the inverse matrix of a() (a^-1) and e*((s*I6-a)^-1)*b+f.
2. "you will like the answer" - In principle, I am interested in being able to perform this symbolic calculation (if possible, ie if there is any other way to symbolically calculate the respective inversion in e*(s*I6-a())^-1)*b+ f), as later from the previous equation results in some transfer functions that I am interested in seeing symbolically.
I have attached the Mathcad 11 version file.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Calculating the inverse of that matrix a is a piece of cake for Mathcad 11.
The result is about 50 pages wide.
Below is a picture of the first 24.5 pages:
(unfortunately my screen isn't wide enough to show the entire expression, the zoom is limited down to 10 %, so I can't zoom out any further)
This is the first 3 pages:
This the last 3:
For your convenience, I've copied the symbolic result of the inverse to a new expression, so you can have a look at it in Mathcad 15, in detail.
Needless to say, the result of your final equation was also found, without problems.
It takes up a lot more space than the inverse of a. I've copied the symbolic result to function sol. You can have a look at that as well.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I put the matrix into Maple Flow, and (assuming I typed the equations in correctly) the inverse was calculated pretty easily. Here's the left-hand side of the matrix.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I am not sure what the ultimate aim is here. I post this in case it motivates the desired approach. Anything above N=2 is unwieldy:
Setup:
matg[n_, s_, col_] := Table[Style[Unique[s], col, Bold], {n}]
smat[n_, s_, col_] :=
SparseArray[{i_, j_} :> Style[Unique[s], col, Bold], {n, n}]
Example:
a = smat[2, "a", Red];
b = List /@ matg[2, "b", Darker[Green]];
c = List /@ matg[2, "c", Blue];
mat = ArrayFlatten[{{a, b, c}, {Transpose[b],
Style[Unique["d"], Bold], 0}, {Transpose[c], 0, 0}}];
mat // MatrixForm
With[{det = Det[mat]},
Inverse[mat] /. det -> 1 //
Column[{Row[{1/Det,
Grid[#, Frame -> All, Alignment -> Left, ItemSize -> 10,
Background -> LightYellow]}], Row[{"where Det =", det}]},
ItemSize -> 50, Alignment -> Center] &]
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Too big result. You have to try to make the elements of the matrix very small. For example, if a formula consists only of constants, then you define the constant first and then assign it to an element of the matrix with a short alphanumeric string, and so on for the others. Remembering to reset the symbolic values, that is, for example if the new constant is a0: = ......., then you must set a0: = a0 in order to obtain a symbolic result