Community Tip - Stay updated on what is happening on the PTC Community by subscribing to PTC Community Announcements. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
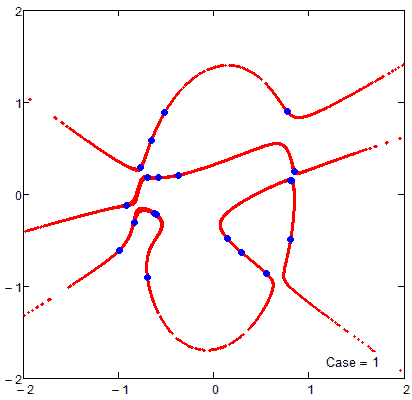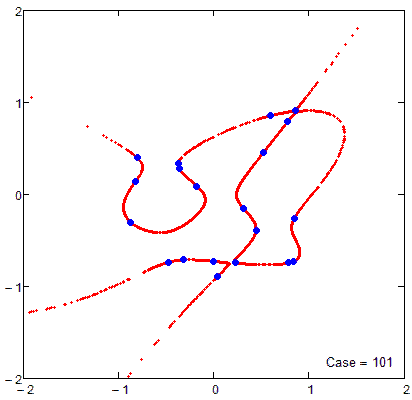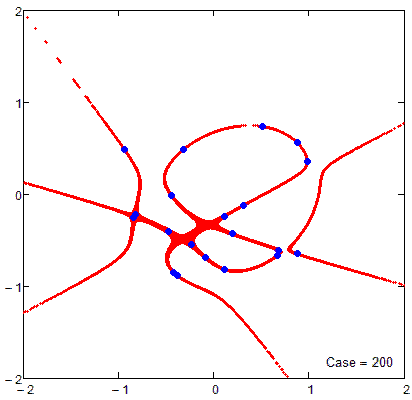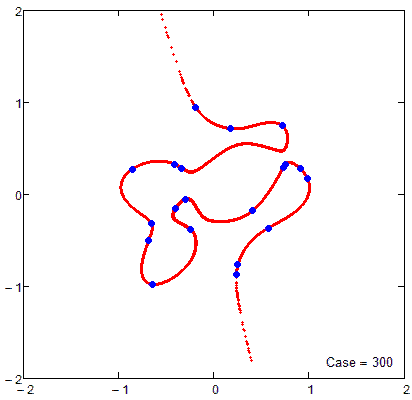
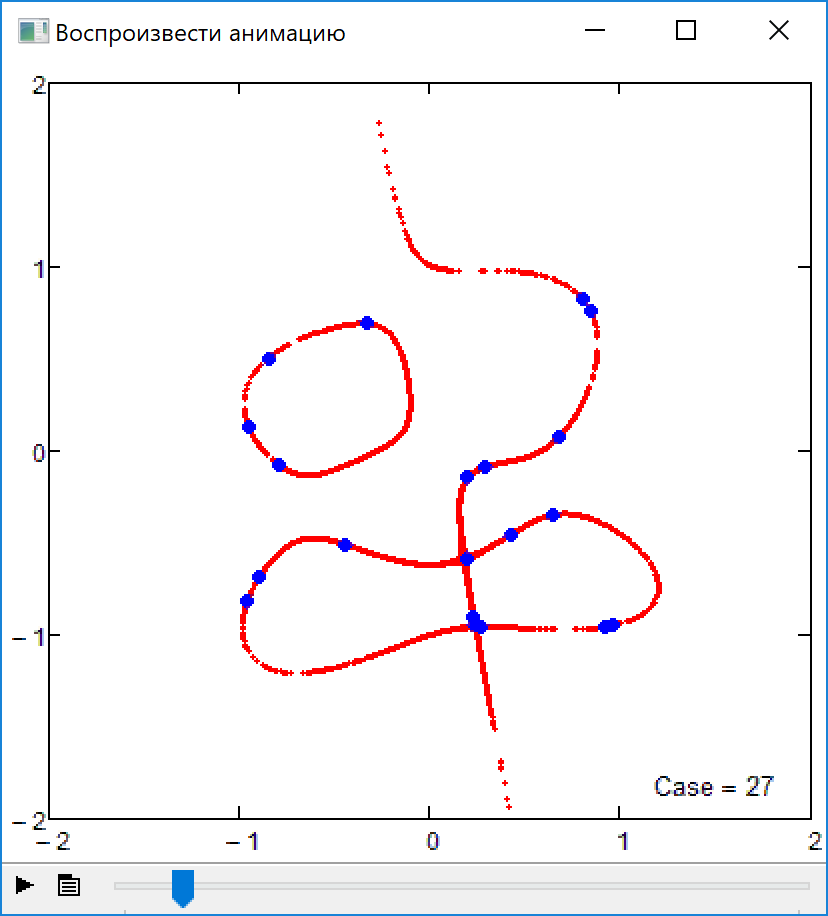
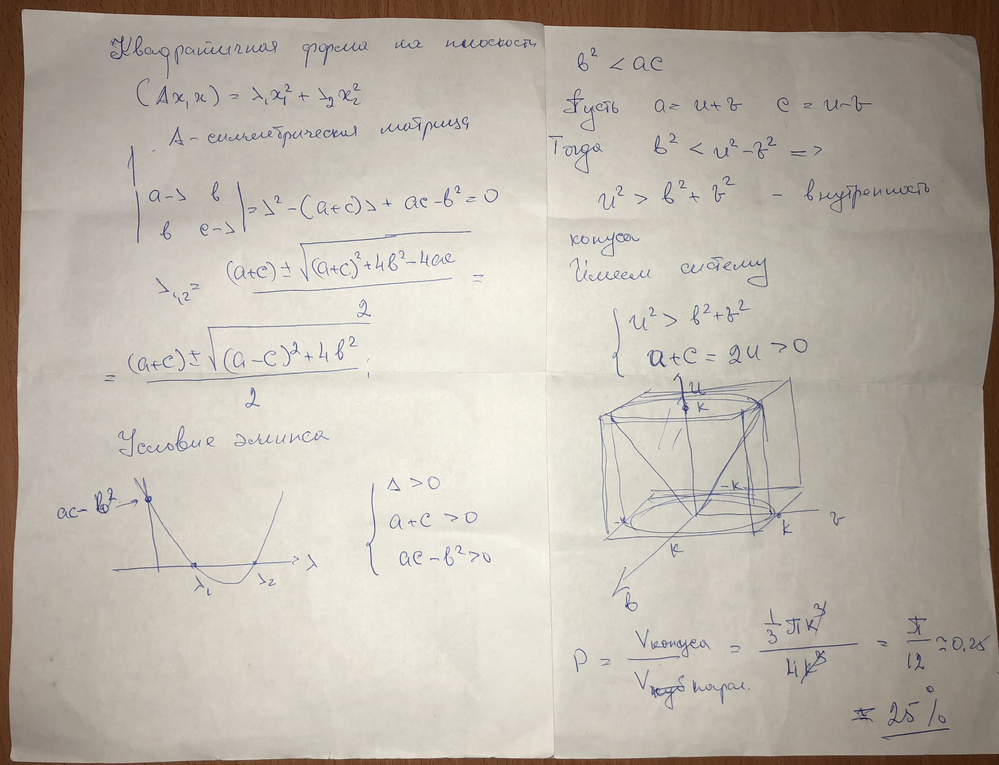
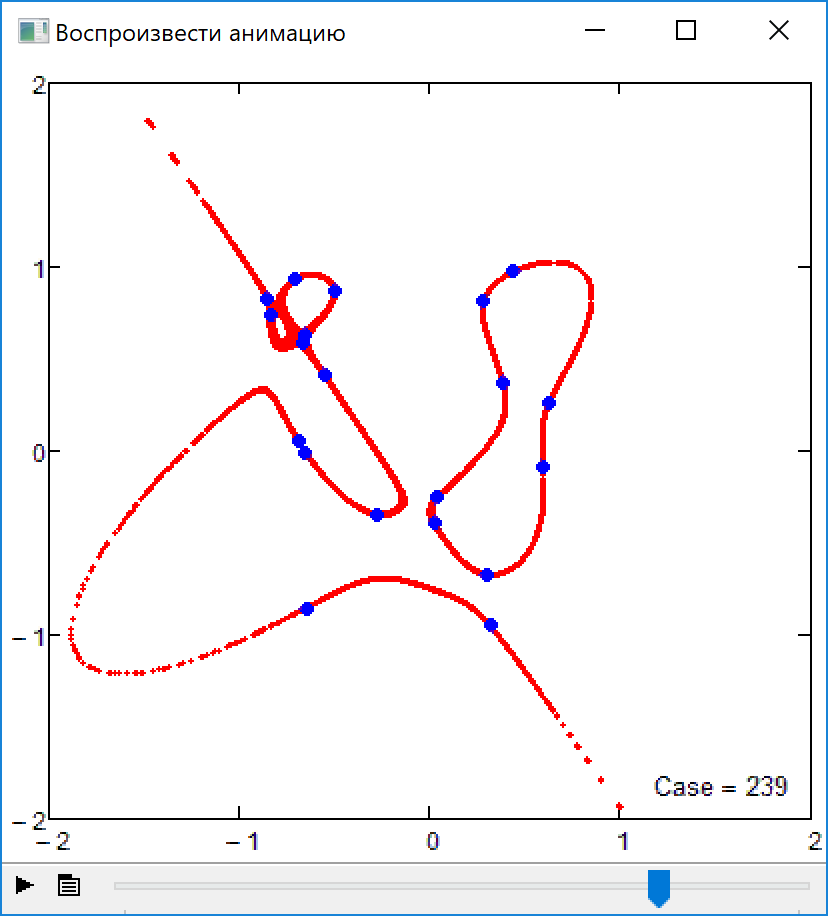
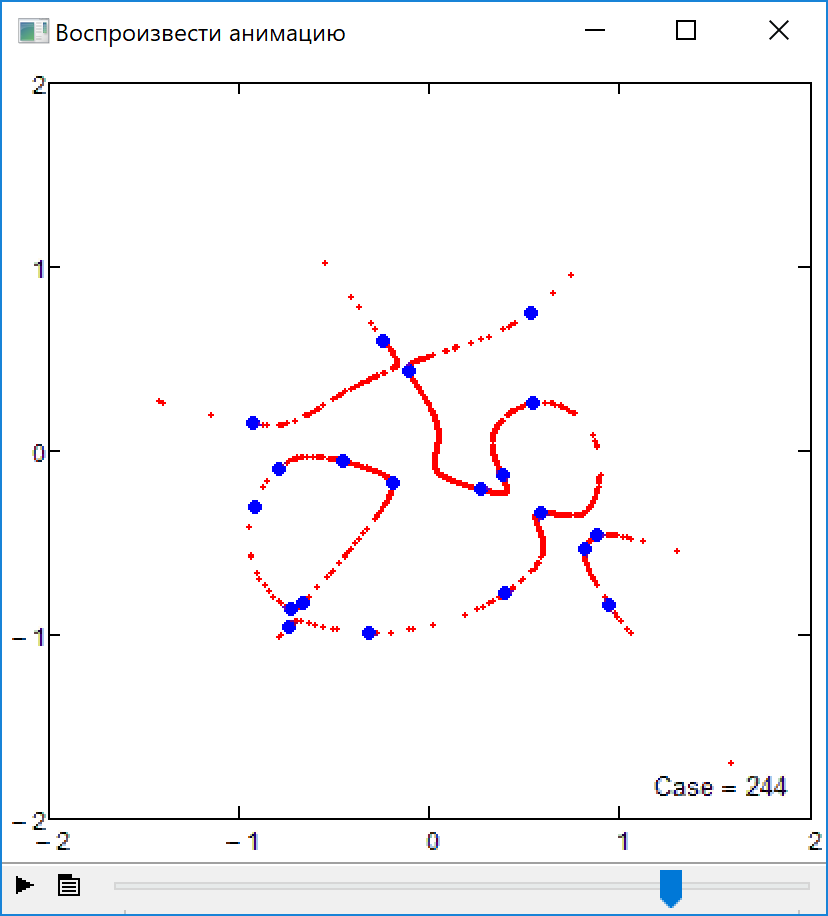
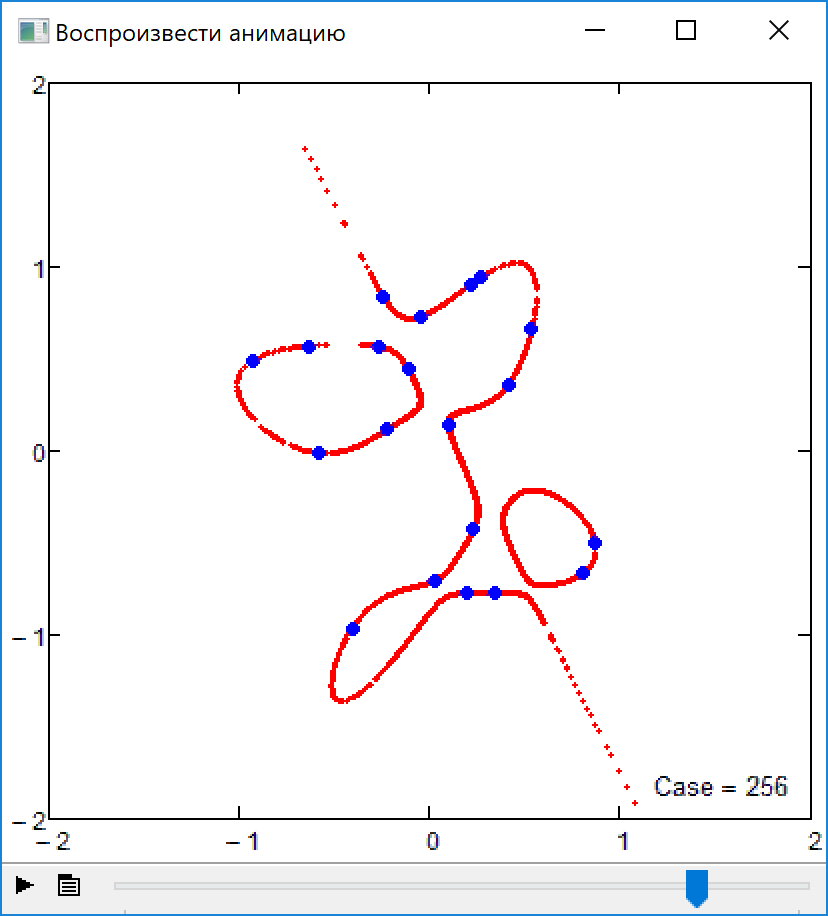
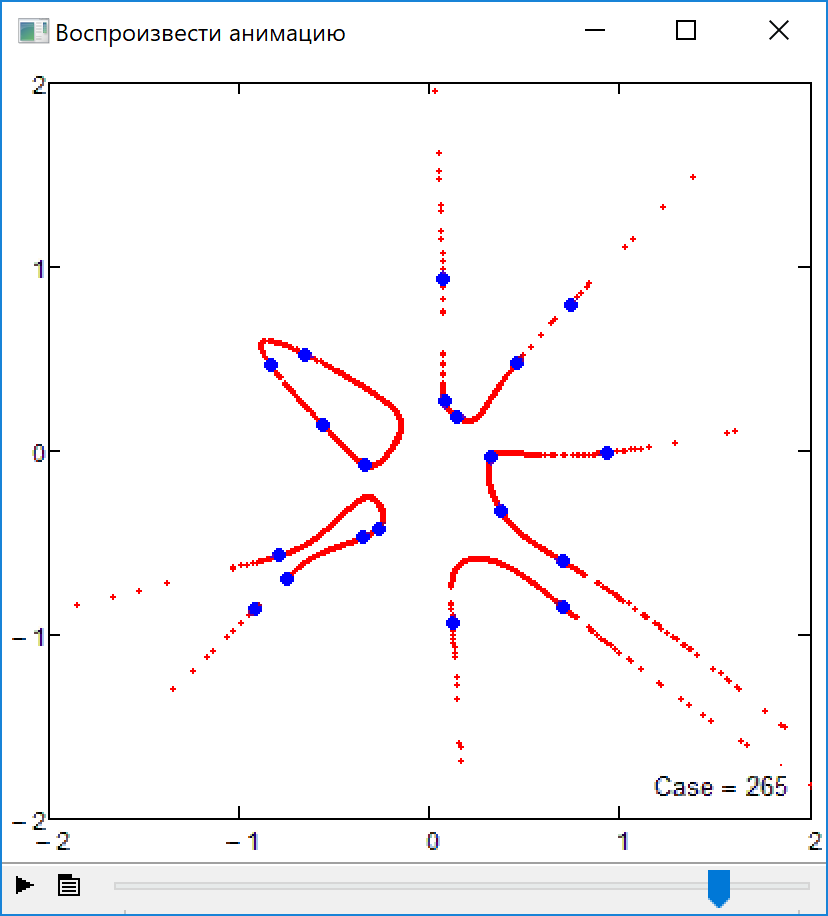
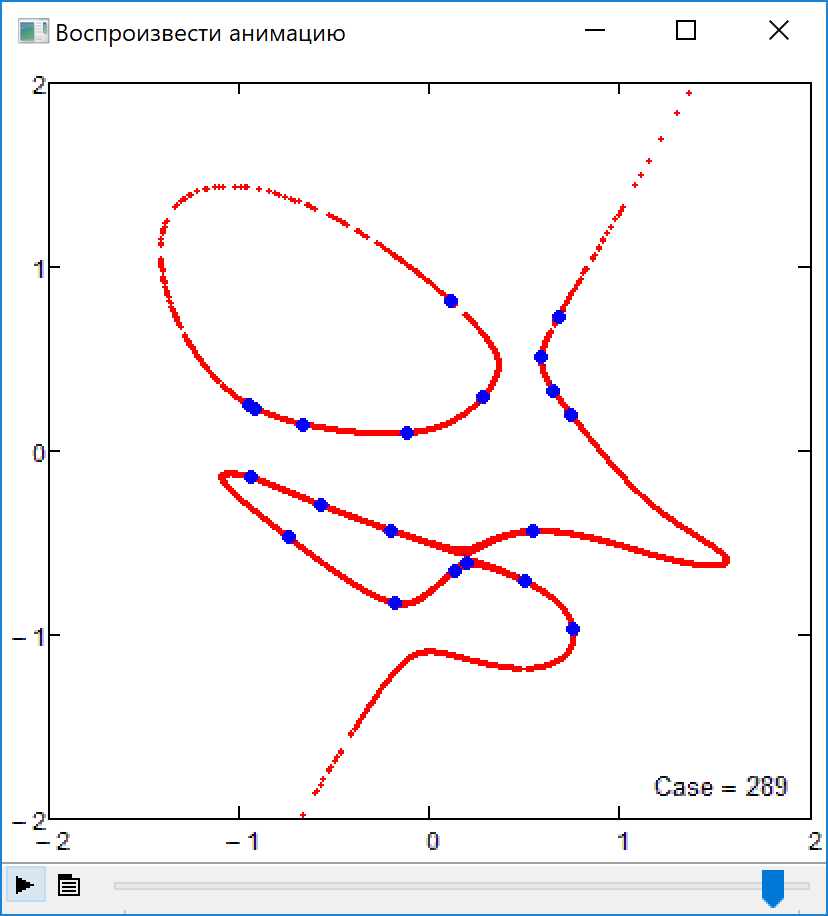
Firecrackers 2018 or 5-th order curve and 20 points
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Firecrackers 2018 or 5-th order curve and 20 points
Self-portrait of Pablo Picasso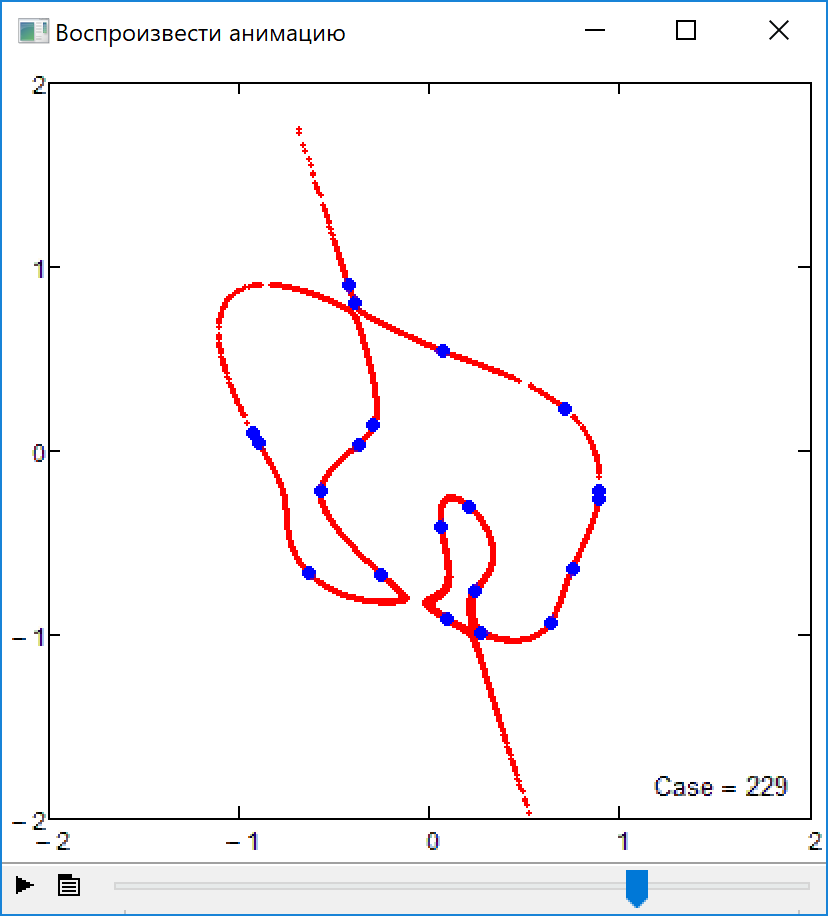

Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery: Beautiful curves! But I'm really replying to your New Year posting about Ochkov's constant (the ellipse fraction in conics through five random points in a square), with value 0.280... Maybe our colleagues have already provided a solution but I have spent many entertaining hours on this problem over the last month and it seems hard to me. One has the distributions of the points and wants the distribution of the discriminant of the solved linear system; well, since your points are chosen independently, the rows of your matrix M are independent, but solving for the five coefficients tangles up the ten independent uniform variables so thoroughly that it gets very hard to see how the original uniform inputs are reflected in the first three coefficients. My first thought was: well, let us pick four points and see what we can learn about the ellipse/hyperbola outcome when we move the fifth point around. Through four points (let's assume the quadrilateral is convex, since if it isn't we already know that we'll get a hyperbola no matter where we put the fifth point) we can draw exactly two parabolas, and they divide our square into ellipse regions and hyperbola regions, as shown in the attached pdfs. This is cute, but not immediately helpful. Note that an extra layer of complexity comes from the uniform distributions which, since they are step functions, propagate annoying edges throughout the computation. I've looked at simpler versions (let us say radially normally distributed, so the we get rid of the edges and have some symmetry to exploit) but eventually I run into the same wall, perhaps disguised as a different wall.
Anyhow, I'm enjoying getting re-acquainted with Mathcad via version 15. I worked at Mathsoft roughly from version 1.5 through 11 and remember that you were one of our earliest supporters, so I'm glad to see that you are still a Mathcad advocate, and I look forward to participating in the community (...once the ellipse constant problem is solved, that is).
Best from Chicago, where we just pretend to have winter.
Frank Purcell
twinprime@att.net
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery: Beautiful curves! But I'm really replying to your New Year posting about Ochkov's constant (the ellipse fraction in conics through five random points in a square), with value 0.280... Maybe our colleagues have already provided a solution but I have spent many entertaining hours on this problem over the last month and it seems hard to me. One has the distributions of the points and wants the distribution of the discriminant of the solved linear system; well, since your points are chosen independently, the rows of your matrix M are independent, but solving for the five coefficients tangles up the ten independent uniform variables so thoroughly that it gets very hard to see how the original uniform inputs are reflected in the first three coefficients. My first thought was: well, let us pick four points and see what we can learn about the ellipse/hyperbola outcome when we move the fifth point around. Through four points (let's assume the quadrilateral is convex, since if it isn't we already know that we'll get a hyperbola no matter where we put the fifth point) we can draw exactly two parabolas, and they divide our square into ellipse regions and hyperbola regions, as shown in the attached pdfs. This is cute, but not immediately helpful. Note that an extra layer of complexity comes from the uniform distributions which, since they are step functions, propagate annoying edges throughout the computation. I've looked at simpler versions (let us say radially normally distributed, so the we get rid of the edges and have some symmetry to exploit) but eventually I run into the same wall, perhaps disguised as a different wall.
Anyhow, I'm enjoying getting re-acquainted with Mathcad via version 15. I worked at Mathsoft roughly from version 1.5 through 11 and remember that you were one of our earliest supporters, so I'm glad to see that you are still a Mathcad advocate, and I look forward to participating in the community (...once the ellipse constant problem is solved, that is).
Best from Chicago, where we just pretend to have winter.
Frank Purcell
twinprime@att.net
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Frank!
Now I am preparing an article on this problem.
Let do it together!
Val
The begin of the article
В стародавние времена путешествие по Свету могли позволить себе только очень богатые и физически здоровые люди. Сейчас же это удовольствие доступно очень многим, а не только избранным: сел в самолет, автомобиль или на поезд – и за короткое время с комфортом ты можешь добраться практически до любого уголка Земли.
Такой же прогресс наблюдается в отношении и… математики. Раньше в ее интереснейшие дебри могли забираться только избранные люди – люди с особыми математическими способностями (с «математическим слухом») и получившие соответствующее математическое образование. Но в настоящее время круг таких «избранных» существенно расширился за счет появления… компьютерных математических пакетов, которые облегчают путешествие в мир математики, делают его массовым.
И еще одно вводное замечание.
Для чего изучают математику в школе и в вузе.
Во-первых, для того, чтобы можно было освоить другие учебные дисциплины: физику, химию, теоретическую механику, гидрогазодинамику, сопротивление материалов, инженерную графику, экономику и т.д.
Во-вторых, нужно всегда помнить, что математика – это лучшая гимнастика (фитнесс) для ума. Изучая математику, мы развиваем свои умственные способности, которые пригодятся нам при решении не только математических, но и разных производственных и житейских задач.
И в-третьих, изучение математики – это само по себе интересное и увлекательное занятие, которым можно заниматься как хобби. Но без математических компьютерных пакетов это делать было почти невозможно, если, повторяем, нет особых математических талантов и соответствующего математического образования.
Why do we study mathematics at school and at a university.
First, in order to be able to master other disciplines: physics, chemistry, theoretical mechanics, fluid dynamics, material resistance, engineering graphics, economics, etc.
And thirdly, the study of mathematics - this in itself is an interesting and fascinating occupation, which you can do as a hobby. But without mathematical computer packages, it was almost impossible to do this, if, we repeat, there are no special mathematical talents and the corresponding mathematical education.
.
.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@twinprime wrote:
Valery: Beautiful curves! But I'm really replying to your New Year posting about Ochkov's constant (the ellipse fraction in conics through five random points in a square), with value 0.280...
Thanks one more and sorry.
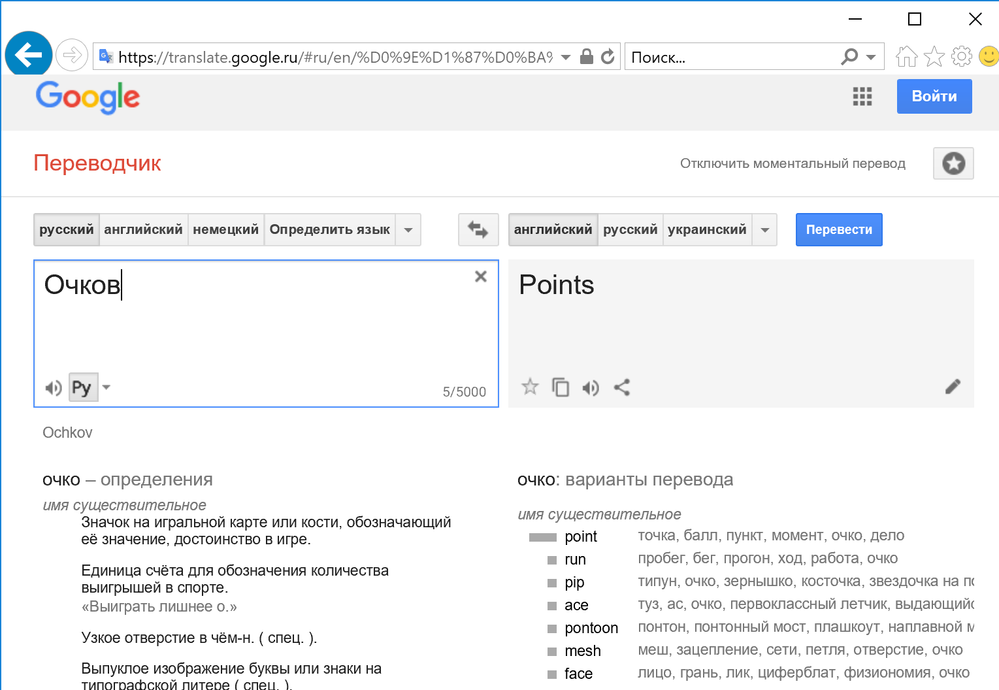
It is not the Ochkov's constant - it if the Points's constant!
Why?
The google translator translates into English my name Очков as... Points 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
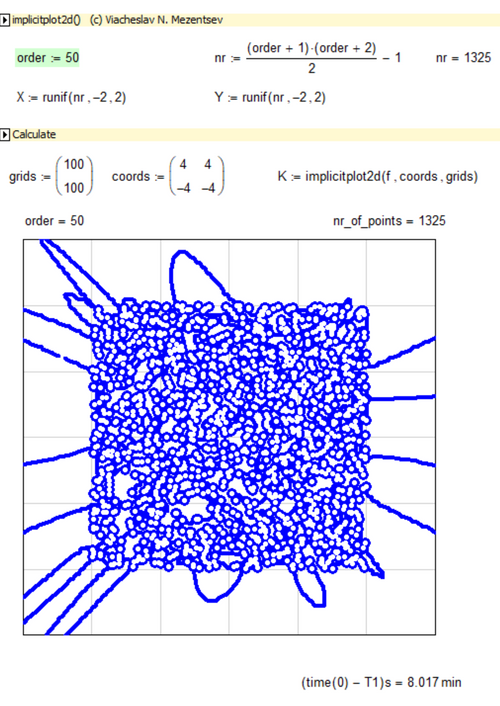
I forgot about the promised sheet which would also show algebraic curves of higher orders you asked for a while ago. Here its is- The limit of order 17 is gone now (was a silly mistake of mine) and now the limit is just the memory Mathcad 15 would be able to use for its matrices and calculations. And of course the limit is your patience - the order-50 curve in the pic needed more than 8 minutes to finish.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Werner_E wrote:
I forgot about the promised sheet which would also show algebraic curves of higher orders you asked for a while ago. Here its is- The limit of order 17 is gone now (was a silly mistake of mine) and now the limit is just the memory Mathcad 15 would be able to use for its matrices and calculations. And of course the limit is your patience - the order-50 curve in the pic needed more than 8 minutes to finish.
I must edit the article!
Let do it together!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Its a pity that my time is so limited.
I think algebraic curves of higher order aren't of much interest in this context. It was just a challenge to implement a way to do it without having to rewrite the whole sheet for a different order.
I think that the Ochkov/Point![]() constant is far more interesting but I can't think of a way to calculate it other than a simulation. I guess Frank Purcell is on a good way and I am looking forward at his further efforts.
constant is far more interesting but I can't think of a way to calculate it other than a simulation. I guess Frank Purcell is on a good way and I am looking forward at his further efforts.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Werner_E wrote:
I think that the Ochkov/Point constant is far more interesting
Thanks, Werner!
But more correct V Points constant - Five Points constant: V - Valery and Roman five ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
We can (better?) work not with a square but with a circle!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This constant (Hyperbola-Ellipse and 5 points) may by has the value Pi/12 (a solution by A.G. Eliseev):
See also https://dxdy.ru/topic129587.html