Community Tip - Have a PTC product question you need answered fast? Chances are someone has asked it before. Learn about the community search. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
First-order boundary value problem
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
First-order boundary value problem
Hi everyone,
I am trying to solve nonlinear eigenproblem of lubrication theory, in the problem two boundat conditions are given at each end points. Since it is a first order boundary value problem so i solved it with normal intial value problem using AdamsBDS solver. However my solution is incorrect. The detail problem and my solution is attached. Kindly suggest me the solution.
Thank you
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You can solve as an ODE simply by starting at b and integrating back to a. However, with an epsilon of 0.1 the value of y(a) is 0.982. To get y(a) closer to 1 use a smaller epsilon (though I guess this makes it a different problem!). See attached.
Alan
PS epsilon should divide the whole of the right-hand side of D, not just the first term as you have it in your image above.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
See (Search/Find) please in Mathcad Prime help the topic "Boundary Problem"!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you Valery Ochkov. I tried to search from the help topic, and follow the syntax mentioned in one of the case study given in help section, but that is given for 2nd order boundary value problem, my case is the 1st order boundary value problem. Now am having some sntax error in sbval, "this function cannot be used here'. The new solution file is attached.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You can solve as an ODE simply by starting at b and integrating back to a. However, with an epsilon of 0.1 the value of y(a) is 0.982. To get y(a) closer to 1 use a smaller epsilon (though I guess this makes it a different problem!). See attached.
Alan
PS epsilon should divide the whole of the right-hand side of D, not just the first term as you have it in your image above.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dear Alan Stevens
Thanks a lot for the comprehensive reply. I got your point, I checked my file by using b to a, its ok now.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You can't force two boundary conditions in this first order DE, so you must decide at which end you begin. Sometimes the results are quite different depending on the end you begin integration. Starting at b gives you (roughly) the result you are aiming for, but the first condition is not matched perfectly.
If you switch a and b in the call to AdamsBDF the results differs significantly.
BTW, you missed an epsilon in your equation in the second term.
[EDIT: Just saw that Alan already pointed that out]
"sbval" would be uses for systems of DE or a higher order DE. If you had a second order DE you could demand y(a)=y(b)=1. But most numeric solvers dont like the initial conditions at two different points but would rather insist in something like y(a)=1 and y'(a)=???. sbval helps you to finde the ???.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you Wrner Exinger for your detailed reply, it is very helpful for me.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
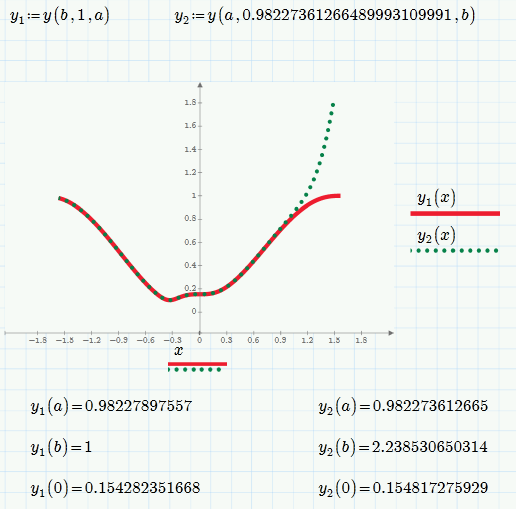
The DE seems to be very sensible with respect to the initial value.
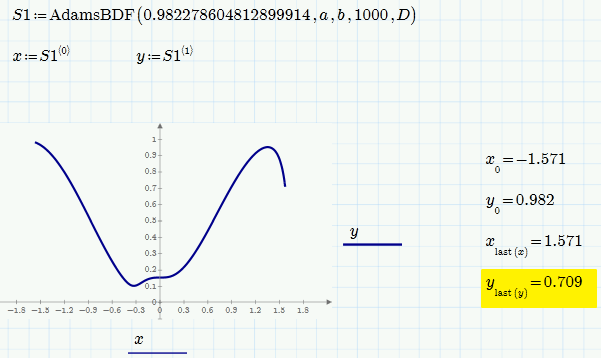
Playing around with Alan's sheet I found that by chosing an appropriate start value we can even solve "forward" and get a similar result as solving backwards (at least for the first 80% of the interval. The value given seems to be the minimum value possible. Change the last 1 to a 0 and odesolve fails.
Similar with AdamsBDF - but the start value and the result differs. Haven't tried oder solvers.
So I guess that y(a)=y(b)=1 is not possible to achieve with this DE, at least not with the given values of lamda and epsilon. .
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
To understand this behaviour you have to consider the sign of D = (sin(x)^2 -lambda.sin(x)^4/y(x))/e when x is -pi/2 and +pi/2. At each value of x both sin(x)^2 and sin(x)^4 are 1. Since lambda is 1 then, if y is 1, D is zero; i.e. the gradient at each end is zero. Hence extrapolating forward from x = -pi/2, or backward from x = +pi/2, by a small distance dx, we still get y(new value of x) = 1.
Now, the value of D at the new value of x is no longer zero, because the (absolute value of the) sine of the new value of x is a little smaller than 1. This means sin(x)^4 is smaller than sin(x)^2, so, with y still 1, the new gradient (value of D) is positive.
Moving further towardsthe right from x = –pi/2 with a positive gradient means starting to curve upwards. Moving further towards the left from x = +pi/2 with a positive gradient means starting to curve downwards (a positive gradient means increase to the right and decrease to the left).
With an initial value of y at x = -pi/2 of 0.982 or thereabouts the initial value of D is negative and the curve turns downward as desired.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for the explanation, lan. Crisp and clear as usual. Odesolve fails if we go below (-pi/2; 0.98227...) because there seems to be no way to go further to the left. Not sure if this range between 0.98227.. and 1 exists for the exact solution, too or if its just due to numerical inaccuracies.
Her is the slopefield for this DE.


- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
And what about shoting
Sure, why don't you apply your suggested method to the very DE in question here and show what you come up with?





